Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – October 23, 2010 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
A budget deficit equivalent to 3 per cent of GDP signals that the government is adopting a less expansionary policy than if the budget deficit outcome was equivalent to 5 per cent of GDP.
The answer is Maybe.
The question probes an understanding of the forces (components) that drive the budget balance that is reported by government agencies at various points in time.
In outright terms, a budget deficit that is equivalent to 5 per cent of GDP is more expansionary than a budget deficit outcome that is equivalent to 3 per cent of GDP. But that is not what the question asked. The question asked whether that signalled that the government is adopting a less expansionary policy – that is, whether its discretionary fiscal intent was expansionary.
In other words, what does the budget outcome signal about the discretionary fiscal stance adopted by the government.
To see the difference between these statements we have to explore the issue of decomposing the observed budget balance into the discretionary (now called structural) and cyclical components. The latter component is driven by the automatic stabilisers that are in-built into the budget process.
The federal (or national) government budget balance is the difference between total federal revenue and total federal outlays. So if total revenue is greater than outlays, the budget is in surplus and vice versa. It is a simple matter of accounting with no theory involved. However, the budget balance is used by all and sundry to indicate the fiscal stance of the government.
So if the budget is in surplus it is often concluded that the fiscal impact of government is contractionary (withdrawing net spending) and if the budget is in deficit we say the fiscal impact expansionary (adding net spending).
Further, a rising deficit (falling surplus) is often considered to be reflecting an expansionary policy stance and vice versa. What we know is that a rising deficit may, in fact, indicate a contractionary fiscal stance – which, in turn, creates such income losses that the automatic stabilisers start driving the budget back towards (or into) deficit.
So the complication is that we cannot conclude that changes in the fiscal impact reflect discretionary policy changes. The reason for this uncertainty clearly relates to the operation of the automatic stabilisers.
To see this, the most simple model of the budget balance we might think of can be written as:
Budget Balance = Revenue – Spending.
Budget Balance = (Tax Revenue + Other Revenue) – (Welfare Payments + Other Spending)
We know that Tax Revenue and Welfare Payments move inversely with respect to each other, with the latter rising when GDP growth falls and the former rises with GDP growth. These components of the budget balance are the so-called automatic stabilisers.
In other words, without any discretionary policy changes, the budget balance will vary over the course of the business cycle. When the economy is weak – tax revenue falls and welfare payments rise and so the budget balance moves towards deficit (or an increasing deficit). When the economy is stronger – tax revenue rises and welfare payments fall and the budget balance becomes increasingly positive. Automatic stabilisers attenuate the amplitude in the business cycle by expanding the budget in a recession and contracting it in a boom.
So just because the budget goes into deficit or the deficit increases as a proportion of GDP doesn’t allow us to conclude that the Government has suddenly become of an expansionary mind. In other words, the presence of automatic stabilisers make it hard to discern whether the fiscal policy stance (chosen by the government) is contractionary or expansionary at any particular point in time.
To overcome this uncertainty, economists devised what used to be called the Full Employment or High Employment Budget. In more recent times, this concept is now called the Structural Balance. The Full Employment Budget Balance was a hypothetical construct of the budget balance that would be realised if the economy was operating at potential or full employment. In other words, calibrating the budget position (and the underlying budget parameters) against some fixed point (full capacity) eliminated the cyclical component – the swings in activity around full employment.
So a full employment budget would be balanced if total outlays and total revenue were equal when the economy was operating at total capacity. If the budget was in surplus at full capacity, then we would conclude that the discretionary structure of the budget was contractionary and vice versa if the budget was in deficit at full capacity.
The calculation of the structural deficit spawned a bit of an industry in the past with lots of complex issues relating to adjustments for inflation, terms of trade effects, changes in interest rates and more.
Much of the debate centred on how to compute the unobserved full employment point in the economy. There were a plethora of methods used in the period of true full employment in the 1960s. All of them had issues but like all empirical work – it was a dirty science – relying on assumptions and simplifications. But that is the nature of the applied economist’s life.
As I explain in the blogs cited below, the measurement issues have a long history and current techniques and frameworks based on the concept of the Non-
Accelerating Inflation Rate of Unemployment (the NAIRU) bias the resulting analysis such that actual discretionary positions which are contractionary are seen as being less so and expansionary positions are seen as being more expansionary.
The result is that modern depictions of the structural deficit systematically understate the degree of discretionary contraction coming from fiscal policy.
So the data provided by the question could indicate a more expansionary fiscal intent from government but it could also indicate a large automatic stabiliser (cyclical) component.
Therefore the best answer is Maybe because there are circumstances where the proposition will not hold. It doesn’t always hold.
You might like to read these blogs for further information:
Question 2:
When the government borrows from the private sector to match an increase in net public spending, the resulting increase in aggregate demand is less than would be the case if there was no bond sale.
The answer is false.
The mainstream macroeconomic textbooks all have a chapter on fiscal policy (and it is often written in the context of the so-called IS-LM model but not always).
The chapters always introduces the so-called Government Budget Constraint that alleges that governments have to “finance” all spending either through taxation; debt-issuance; or money creation. The writer fails to understand that government spending is performed in the same way irrespective of the accompanying monetary operations.
The textbook argument claims that money creation (borrowing from central bank) is inflationary while the latter (private bond sales) is less so. These conclusions are based on their erroneous claim that “money creation” adds more to aggregate demand than bond sales, because the latter forces up interest rates which crowd out some private spending.
All these claims are without foundation in a fiat monetary system and an understanding of the banking operations that occur when governments spend and issue debt helps to show why.
So what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a budget deficit without issuing debt?
Like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.
The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made.
Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet).
Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.
This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management. The aim of the central bank is to “hit” a target interest rate and so it has to ensure that competitive forces in the interbank market do not compromise that target.
When there are excess reserves there is downward pressure on the overnight interest rate (as banks scurry to seek interest-earning opportunities), the central bank then has to sell government bonds to the banks to soak the excess up and maintain liquidity at a level consistent with the target.
Some central banks offer a return on overnight reserves which reduces the need to sell debt as a liquidity management operation.
There is no sense that these debt sales have anything to do with “financing” government net spending. The sales are a monetary operation aimed at interest-rate maintenance.
So M1 (deposits in the non-government sector) rise as a result of the deficit without a corresponding increase in liabilities. It is this result that leads to the conclusion that that deficits increase net financial assets in the non-government sector.
What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.
The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).
There is no difference to the impact of the deficits on net worth in the non-government sector.
Mainstream economists would say that by draining the reserves, the central bank has reduced the ability of banks to lend which then, via the money multiplier, expands the money supply.
However, the reality is that:
- Building bank reserves does not increase the ability of the banks to lend.
- The money multiplier process so loved by the mainstream does not describe the way in which banks make loans.
- Inflation is caused by aggregate demand growing faster than real output capacity. The reserve position of the banks is not functionally related with that process.
So the banks are able to create as much credit as they can find credit-worthy customers to hold irrespective of the operations that accompany government net spending.
This doesn’t lead to the conclusion that deficits do not carry an inflation risk. All components of aggregate demand carry an inflation risk if they become excessive, which can only be defined in terms of the relation between spending and productive capacity.
It is totally fallacious to think that private placement of debt reduces the inflation risk. It does not.
You may wish to read the following blogs for more information:
- Why history matters
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- The complacent students sit and listen to some of that
Question 3:
If the external balance remains in surplus, then the national government will not impede economic growth by running a budget surplus.
The answer is false.
First, you need to understand the basic relationship between the sectoral flows and the balances that are derived from them. The flows are derived from the National Accounting relationship between aggregate spending and income. So:
(1) Y = C + I + G + (X – M)
where Y is GDP (income), C is consumption spending, I is investment spending, G is government spending, X is exports and M is imports (so X – M = net exports).
Another perspective on the national income accounting is to note that households can use total income (Y) for the following uses:
(2) Y = C + S + T
where S is total saving and T is total taxation (the other variables are as previously defined).
You than then bring the two perspectives together (because they are both just “views” of Y) to write:
(3) C + S + T = Y = C + I + G + (X – M)
You can then drop the C (common on both sides) and you get:
(4) S + T = I + G + (X – M)
Then you can convert this into the familiar sectoral balances accounting relations which allow us to understand the influence of fiscal policy over private sector indebtedness.
So we can re-arrange Equation (4) to get the accounting identity for the three sectoral balances – private domestic, government budget and external:
(S – I) = (G – T) + (X – M)
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.
Another way of saying this is that total private savings (S) is equal to private investment (I) plus the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
Thus, when an external deficit (X – M < 0) and public surplus (G – T < 0) coincide, there must be a private deficit. While private spending can persist for a time under these conditions using the net savings of the external sector, the private sector becomes increasingly indebted in the process.
Second, you then have to appreciate the relative sizes of these balances to answer the question correctly.
Consider the following Table which depicts three cases – two that define a state of macroeconomic equilibrium (where aggregate demand equals income and firms have no incentive to change output) and one (Case 2) where the economy is in a disequilibrium state and income changes would occur.
Note that in the equilibrium cases, the (S – I) = (G – T) + (X – M) whereas in the disequilibrium case (S – I) > (G – T) + (X – M) meaning that aggregate demand is falling and a spending gap is opening up. Firms respond to that gap by decreasing output and income and this brings about an adjustment in the balances until they are back in equality.
So in Case 1, assume that the private domestic sector desires to save 2 per cent of GDP overall (spend less than they earn) and the external sector is running a surplus equal to 4 per cent of GDP.
In that case, aggregate demand will be unchanged if the government runs a surplus of 2 per cent of GDP (noting a negative sign on the government balance means T > G).
In this situation, the surplus does not undermine economic growth because the injections into the spending stream (NX) are exactly offset by the leakages in the form of the private saving and the budget surplus. This is the Norwegian situation.
In Case 2, we hypothesise that the private domestic sector now wants to save 6 per cent of GDP and they translate this intention into action by cutting back consumption (and perhaps investment) spending.
Clearly, aggregate demand now falls by 4 per cent of GDP and if the government tried to maintain that surplus of 2 per cent of GDP, the spending gap would start driving GDP downwards.
The falling income would not only reduce the capacity of the private sector to save but would also push the budget balance towards deficit via the automatic stabilisers. It would also push the external surplus up as imports fell. Eventually the income adjustments would restore the balances but with lower GDP overall.
So Case 2 is a not a position of rest – or steady growth. It is one where the government sector (for a given net exports position) is undermining the changing intentions of the private sector to increase their overall saving.
In Case 3, you see the result of the government sector accommodating that rising desire to save by the private sector by running a deficit of 2 per cent of GDP.
So the injections into the spending stream are 4 per cent from NX and 2 per cent from the deficit which exactly offset the desire of the private sector to save 6 per cent of GDP. At that point, the system would be in rest.
This is a highly stylised example and you could tell a myriad of stories that would be different in description but none that could alter the basic point.
If the drain on spending outweighs the injections into the spending stream then GDP falls (or growth is reduced).
So even though an external surplus is being run, the desired budget balance still depends on the saving desires of the private domestic sector. Under some situations, these desires could require a deficit even with an external surplus.
You may wish to read the following blogs for more information:
- Back to basics – aggregate demand drives output
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
- Barnaby, better to walk before we run
- Saturday Quiz – June 19, 2010 – answers and discussion
Question 4:
Fiscal rules such as are embodied in the Stability and Growth Pact of the EMU will continually create conditions of slower growth because they deprive the government of fiscal flexibility to support aggregate demand when necessary.
The answer is False.
One word in the question renders this proposition false. I had originally worded the question (following EMU) “will bias the nations to slower growth” etc which is true and I considered that too easy.
The fiscal policy rules that were agreed in the Maastricht Treaty – budget deficits should not exceed 3 per cent of GDP and public debt should not exceed 60 per cent of GDP – clearly constrain EMU governments during periods when private spending (or net exports) are draining aggregate demand.
In those circumstances, if the private spending withdrawal is sufficiently severe, the automatic stabilisers alone will drive the budget deficit above the required limits. Pressure then is immediately placed on the national governments to introduce discretionary fiscal contractions to get the fiscal balance back within the limits.
Further, after an extended recession, the public debt ratios will almost always go beyond the allowable limits which places further pressure on the government to introduce an extended period of austerity to bring the ratio back within the limits. So the bias is towards slower growth overall.
It is also true that the fiscal rules clearly (and by design) “deprive the government of fiscal flexibility to support aggregate demand when necessary”. But that wasn’t the question. The question was will these rules continually create conditions of slower growth. The answer is no they will not.
Imagine a situation where the nation has very strong net exports adding to aggregate demand which supports steady growth and full employment without any need for the government to approach the Maastricht thresholds. In this case, the fiscal rules are never binding unless something happens to exports.
The following is an example of this sort of nation. It will take a while for you to work through but it provides a good learning environment for understanding the basic expenditure-income model upon with Modern Monetary Theory (MMT) builds its monetary insights. You might want to read this blog – Back to basics – aggregate demand drives output – to refresh your understanding of the sectoral balances.
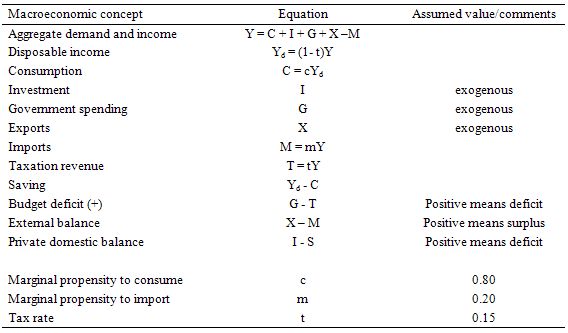
The following Table shows the structure of the simple macroeconomic model that is the foundation of the expenditure-income model. This sort of model is still taught in introductory macroeconomics courses before the students get diverted into the more nonsensical mainstream ideas. All the assumptions with respect to behavioural parameters are very standard. You can download the simple spreadsheet if you want to play around with the model yourselves.
The first Table shows the model structure and any behavioural assumptions used. By way of explanation:
- All flows are in real terms with the price level constant (set at whatever you want it to be). So we are assuming that there is capacity within the supply-side of the economy to respond in real terms when nominal demand (which also equals real demand) changes.
- We might assume that the economy is at full employment in period 1 and in a state of excess capacity of varying degrees in each of the subsequent periods.
- Fiscal policy dominates monetary policy and the latter is assumed unchanged throughout. The central bank sets the interest rate and it doesn’t move.
- The tax rate is 0.15 throughout – so for every dollar of national income earned 15 cents is taken out in tax.
- The marginal propensity to consume is 0.8 – so for every dollar of disposable income 80 cents is consumed and 20 cents is saved.
- The marginal propensity to import is 0.2 – so for every dollar of national income (Y) 20 cents is lost from the expenditure stream into imports.
You might want to right-click the images to bring them up into a separate window and the print them (on recycled paper) to make it easier to follow the evolution of this economy over the 10 periods shown.
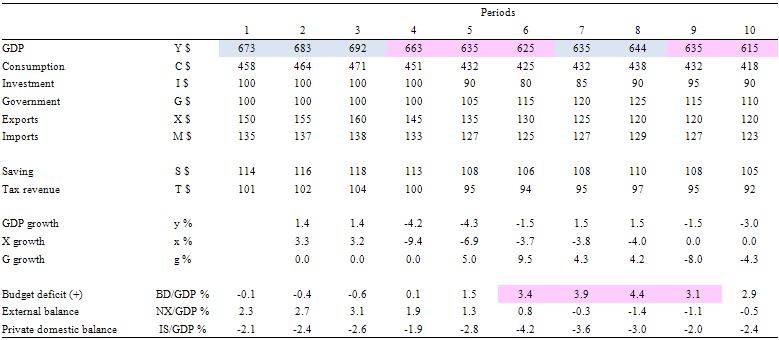
The next table quantifies the ten-period cycle and the graph below it presents the same information graphically for those who prefer pictures to numbers. The description of events is in between the table and the graph for those who do not want to print.
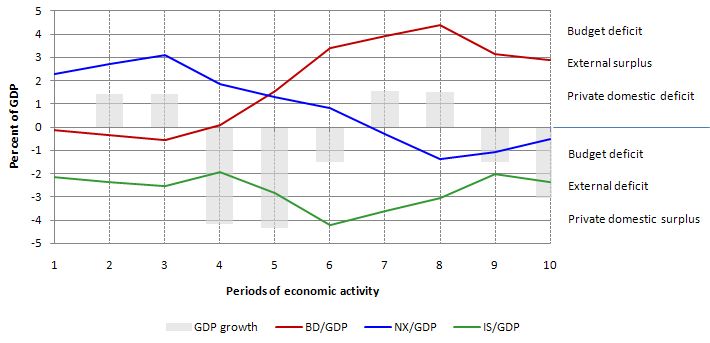
The graph below shows the sectoral balances – budget deficit (red line), external balance (blue line) and private domestic balance (green line) over the 10-period cycle as a percentage of GDP (Y) in addition to the period-by-period GDP growth (y) in percentage terms (grey bars).
Above the zero line means positive GDP growth, a budget deficit (G > T), an external surplus (X > M) and a private domestic deficit (I > S) and vice-versa for below the zero line.
This is an economy that is enjoying steady GDP growth (1.4 per cent) courtesy of a strong and growing export sector (surpluses in each of the first three periods). It is able to maintain strong growth via the export sector which permits a budget surplus (in each of the first three periods) and the private domestic sector is spending less than they are earning.
The budget parameters (and by implication the public debt ratio) is well within the Maastricht rules and not preventing strong (full employment growth) from occurring. You might say this is a downward bias but from in terms of an understanding of functional finance it just means that the government sector is achieving its goals (full employment) and presumably enough services and public infrastructure while being swamped with tax revenue as a result of the strong export sector.
Then in Period 4, there is a global recession and export markets deteriorate up and governments delay any fiscal stimulus. GDP growth plunges and the private domestic balance moves towards deficit. Total tax revenue falls and the budget deficit moves into balance all due to the automatic stabilisers. There has been no discretionary change in fiscal policy.
In Period 5, we see investment expectations turn sour as a reaction to the declining consumption from Period 4 and the lost export markets. Exports continue to decline and the external balance moves towards deficit (with some offset from the declining imports as a result of lost national income). Together GDP growth falls further and we have a technical recession (two consecutive periods of negative GDP growth).
With unemployment now rising (by implication) the government reacts by increasing government spending and the budget moves into deficit but still within the Maastricht rules. Taxation revenue continues to fall. So the increase in the deficit is partly due to the automatic stabilisers and partly because discretionary fiscal policy is now expanding.
Period 6, exports and investment spending decline further and the government now senses a crisis is on their hands and they accelerate government spending. This starts to reduce the negative GDP growth but pushes the deficit beyond the Maastricht limits of 3 per cent of GDP. Note the rising deficits allows for an improvement in the private domestic balance, although that is also due to the falling investment.
In Period 7, even though exports continue to decline (and the external balance moves into deficit), investors feel more confident given the economy is being supported by growth in the deficit which has arrested the recession. We see a return to positive GDP growth in this period and by implication rising employment, falling unemployment and better times. But the deficit is now well beyond the Maastricht rules and rising even further.
In Period 8, exports decline further but the domestic recovery is well under way supported by the stimulus package and improving investment. We now have an external deficit, rising budget deficit (4.4 per cent of GDP) and rising investment and consumption.
At this point the EMU bosses take over and tell the country that it has to implement an austerity package to get their fiscal parameters back inside the Maastricht rules. So in Period 9, even though investment continues to grow (on past expectations of continued growth in GDP) and the export rout is now stabilised, we see negative GDP growth as government spending is savaged to fit the austerity package agree with the EMU bosses. Net exports moves towards surplus because of the plunge in imports.
Finally, in period 10 the EMU bosses are happy in their warm cosy offices in Brussels or Frankfurt or wherever they have their secure, well-paid jobs because the budget deficit is now back inside the Maastricht rules (2.9 per cent of GDP). Pity about the economy – it is back in a technical recession (a double-dip).
Investment spending has now declined again courtesy of last period’s stimulus withdrawal, consumption is falling, government support of saving is in decline, and we would see employment growth falling and unemployment rising.
The following blogs may be of further interest to you:
- Back to basics – aggregate demand drives output
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 5: Premium Question
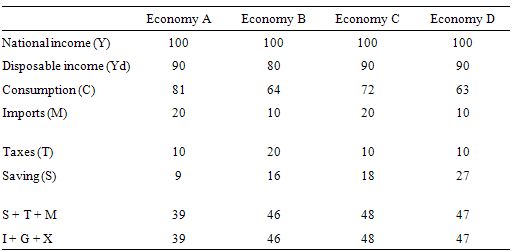
Consider the following table which describes four different economies in terms of the behavioural parameters relating to the leakages to aggregate demand.
Assume that in all four economies, there is idle capacity, the central bank holds all interest rates constant, inflation is constant and there is no changes in international competitiveness.
Which economy would deliver the largest national income bonus for a given discretionary expansion in government spending.
The answer is Economy A.
This question requires you to understand the impact of the different leakages (drains) to aggregate demand that arise from household saving, government taxation and import expenditure.
These leakages combine to determine the spending multiplier.
Students begin to learn about the expenditure multiplier in a very simple model without government or external sector. It sets them up immediately to disregard the crucial relationship between government and non-government sector that really drives the dynamics of the monetary system.
In the text book that Randy Wray and I are currently working on the government/non-government relationship is introduced at the beginning of the learning process to ensure students understand the importance of net positions etc.
So I don’t think it is too hard to explain the expenditure multiplier with government spending, taxes and imports introduced from the start.
The clue is to first of all realise that aggregate demand drives output with generates incomes (via payments to the productive inputs). I won’t go into controversies here about whether the productive inputs are rewarded fairly or whether surplus value is expropriated etc. That is a separate and not unimportant discussion but not germane here to understand the accounting and the dynamics.
Accordingly, what is spent will generate income in that period which is available for use. The uses are further consumption; paying taxes and/or buying imports. We consider imports as a separate category (even though they reflect consumption, investment and government spending decisions) because they constitute spending which does not recycle back into the production process. They are thus considered to be “leakages” from the expenditure system.
So if for every dollar produced and paid out as income, if the economy imports around 20 cents in the dollar, then only 80 cents is available within the system for spending in subsequent periods excluding taxation considerations.
However there are two other “leakages” which arise from domestic sources – saving and taxation. Take taxation first. When income is produced, the households end up with less than they are paid out in gross terms because the government levies a tax. So the income concept available for subsequent spending is called disposable income (Yd).
To keep it simple, imagine a proportional tax of 20 cents in the dollar is levied, so if $100 of income is generated, $20 goes to taxation and Yd is $80 (what is left). So taxation (T) is a “leakage” from the expenditure system in the same way as imports are.
Finally consider saving. Consumers make decisions to spend a proportion of their disposable income. The amount of each dollar they spent at the margin (that is, how much of every extra dollar to they consume) is called the marginal propensity to consume. If that is 0.80 then they spent 80 cents in every dollar of disposable income.
So if total disposable income is $80 (after taxation of 20 cents in the dollar is collected) then consumption (C) will be 0.80 times $80 which is $64 and saving will be the residual – $26. Saving (S) is also a “leakage” from the expenditure system.
It is easy to see that for every $100 produced, the income that is generated and distributed results in $64 in consumption and $36 in leakages which do not cycle back into spending.
For income to remain at $100 in the next period the $36 has to be made up by what economists call “injections” which in these sorts of models comprise the sum of investment (I), government spending (G) and exports (X). The injections are seen as coming from “outside” the output-income generating process (they are called exogenous or autonomous expenditure variables).
Investment is dependent on expectations of future revenue and costs of borrowing. Government spending is clearly a reflection of policy choices available to government. Exports are determined by world incomes and real exchange rates etc.
For GDP to be stable injections have to equal leakages (this can be converted into growth terms to the same effect). The national accounting statements that we have discussed previous such that the government deficit (surplus) equals $-for-$ the non-government surplus (deficit) and those that decompose the non-government sector in the external and private domestic sectors is derived from these relationships.
So imagine there is a certain level of income being produced – its value is immaterial. Imagine that the central bank sees no inflation risk and so interest rates are stable as are exchange rates and domestic wage levels (these simplifications are to to eliminate unnecessary complexity).
The question then is: what would happen if government increased spending by, say, $100? This is the terrain of the multiplier. If aggregate demand increases drive higher output and income increases then the question is by how much?
The spending multiplier is defined as the change in real income that results from a dollar change in exogenous aggregate demand (so one of G, I or X). We could complicate this by having autonomous consumption as well but the principle is not altered.
The spending multiplier is the extra spending that would occur when an autonomous expenditure source changes. So we ask the question: What would be the change in income if I or G or X changed by $1?
To derive the multiplier we need to write out the aggregate demand model and substitute the behavioural parameters into the model.
Aggregate demand (and income)
Y = C + I + G + X – M
Taxes
T = t*Y.
The little t is the marginal tax rate which in this case is the proportional rate. Note here taxes are taken out of total income (Y) which then defines disposable income.
The * sign denotes multiplication. You can do this example in a spreadsheet if you like.
Yd = (1-t)*Y
Consumption and Saving
We define the consumption relationship at the most simple level as a proportional relationship to disposable income (Yd).
C = c*Yd
where little c is the marginal propensity to consume (MPC) or the fraction of every dollar of disposable income consumed.
So using the Yd relationship we can write consumption as:
C = c*(1-t)*Y
Imports
Imports (M) are considered proportional to total income (Y):
M= m*Y
where little m is the marginal propensity to import which is the increase in imports for every real GDP dollar produced.
Multiplier
To derive the multiplier formula we can assemble the aggregate demand relationship with its individual behavioural components as follows:
Y = C + I + G + X – M
Y = c*(1-t)*Y + I + G + X – m*Y
Now, re-arrange the equation to collect the Y terms on the left-hand side:
Y – c*(1-t)*Y + m*Y = I + G + X
You can see the exogenous injections to aggregate demand (those not reliant on national income) are on the right-hand side and all the components of expenditure that rely on national income are collected on the left-hand side.
We simplify this as follows:
Y(1 – c*(1-t)*Y + m) = I + G + X
So the relationship between changes in Y and changes in the exogenous spending components is:
Y = [1/(1 – c*(1-t)*Y + m)]*(I + G + X)
The term in [] brackets on the right-hand side is the multiplier because it shows how much a given change in (I + G + X) multiply to national income Y.
We could write this as:
Y = k*(I + G + X)
where
k = [1/(1 – c*(1-t)*Y + m)]
Or using other symbols:
k = 1/(1 – MPC x (1-t) + MPM)
So the higher is the MPC the lower is the tax rate (t) and the lower is the MPM the higher is the multiplier. That makes sense because taxes and imports drain spending from the income generating system. So as income responds positively to an autonomous injection, the smaller are the drains via taxation and imports and the higher the induced consumption – the higher is the second round spending effect which then continues to generate further income increases.
We can then apply this knowledge to the four economies in the Table. The bottom row of the Table provide the solution to the multiplier for the given parameters.
We interpret the data as follows. If government spending increased by $1, then the total change in national income in Economy A would be $2.56, in Economy B $2.17, in Economy C $2.08, and in Economy D $2.13.
The question obviously requires you to think about the different impacts of varying the drains on aggregate demand. The drains are not all equal.
For example, a given change in the marginal propensity to import has a greater impact than a given change in the marginal propensity to consume as you can see by comparing Economy C to Economy D. This is because imports come out of pre-tax income whereas the consumption decision comes out of disposable income.
A rise in the marginal propensity to consume of 0.1 will more than offset the draining impact of an equal rise in the tax rate because the decline in saving is greater than the rise in taxes.
You can construct all sorts of different scenarios to understand the impacts. To give you an idea of the different compositions of aggregate demand and the different leakages and injections the following Table assumes national income is 100 and then solves the model for each economy given the parameters.
I could clearly make the model more complex but the results would not be very different. Some will suggest the model is overly simplistic because it is a “fixed price” model and assumes supply will just meet any new nominal spending. That is true by construction and is a reasonable description of the state of play at present.
There is no inflation threat at present due to the vast quantities of idle resources that can be brought into production should there be a demand for their services.
Some might argue the external sector is too simplistic and that the terms of trade (real exchange rate) should be included in the export and import relationships. In a complex model that is true but in the context of this model the likely changes would just reinforce the results I derive. There is no loss of insight by holding the terms of trade constant.
Some might argue that the interest rate should be modelled and I reply why? The implicit assumption is that the central bank sets the interest rate and it is currently low in most nations and has been for some years. With no real inflation threat, the short-term rates will remain low for some time yet.
As to long rates (and the rising budget deficit) – show me where the significant rises in budget deficits (for a sovereign nation) are driving up rates. They have actually been falling as a consequence of very strong demand for public debt issues (almost insatiable) by bond markets and the quantitative easing efforts of the large central banks.
For an EMU nation, long-rates are within the control of the ECB as has been demonstrated once it started buying government bonds in the secondary markets. So leaving monetary policy implicit and fixed in this model doesn’t lose any insight or “fix” the results in my favour.
You may wish to read the following blogs for more information:
That is enough for today!



There is a technicality in Q5.
Economy A seems to have a high propensity to consume and it intuitively seems to respond more to an increased government expenditure. Of course, A, B, C and D have different demand leakages and one needs to calculate with an assumed model and it turned out A is right.
However, the multiplier used is a one-period multiplier. If one assumes a propensity to consume out of accumulated wealth as well, it’s highly possible that Economy D’s nation income overtakes Economy A’s income. This is because even though Economy A responds more to the expansion of government expenditures, it also pays higher taxes. Economy D on the other hand, responds slower but the higher deficits keep increasing the private sector wealth and will manage to have a higher national income through consumption out of wealth in addition to consumption out of income
Okay I should have said importing higher instead of saying “paying higher taxes” for economy A. So the analysis was more like comparing B and D.
But doesn’t matter. D’s national income will still overtake A.
Ad 2) Your question specified that the government didn’t sell any bonds. But in your example, the central bank sells bonds. The central bank is just the Treasury in a clown suit, so in your example the consolidated public sector would be issuing bonds, no?
I see the use of decomposing the boost to aggregate demand into a fiscal effect and an interest rate effect. But that seems to be what the orthodox models are groping for as well with their claim that issuing debt is less inflationary than issuing legal tender.
– Jake
Ramanan,
MPC is the propensity to consume – in this case from successive rounds of income created from the initial autonomous injection.
There is no such thing as a “propensity to consume out of accumulated wealth” at the macro level. Macro accumulated wealth doesn’t decline merely because of consumption levels in the current period.
Wealth is effectively the cumulative value of the savings leakage over multiple periods.
I.e. wealth is a cumulative leakage in “technical” terms.
There is no propensity to consume “out of” a leakage – single period or multiple periods.
What you are referring to is the wealth effect.
The wealth effect is simply one input that determines MPC as a parameter.
I.e. the wealth effect is already taken into account in the MPC assumption.
You are suggesting that the wealth effect may some effect on MPC. Yes, but it’s already taken into account in the MPC assumption for each economy. You seem to be suggesting that the MPC assumption may be invalid due to one input, when you don’t know the totality of all of the behavioural inputs that go into determining the stated MPC assumption for each economy.
JKH,
Of course there is such a thing! Stock-flow consistent models use it. If you do not assume such a thing, you run into issues.
The fact that mainstream economists do not use it doesn’t mean that there is no such thing. Modigliani used it.
In fact it could be 0.04 to 0.07 for the United States.
Ramanan,
I meant macro generically, as in global macro.
I suppose you could say the US net consumes from accumulated wealth – in that the current account deficit is effectively reducing accumulated wealth. But since that wealth reduction is offset by an equivalent wealth increase for ROW, there is no net consumption from accumulated wealth at the global macro level.
In any event my comment stands. The wealth effect is a fundamental element already present in the assumed MPC (as well as MPM).
JKH,
Ignore the case of the open economy for the moment. A consumption function usually used is the Keynesian function
C = alpha x YD
Where YD is the household disposable income. (x is for multiplication)
Modigliani proposed a consumption function which is of the form
C = alpha1 x YD + alpha2 x W(-1)
which means the consumption function is both out of income and wealth in the previous period.
Now consumption functions are a matter of debate. However, there is no apriori reason to throw the second term. Google “Life cycle hypothesis”
The problem with the first consumption function is that the wealth/gdp ratio keeps rising forever (and hence the public debt/gdp) which is not what is observed. Perhaps growth stabilizes this ratio but need not be sufficient to explain.
“Like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.”
Let’s say the gov’t makes a $1,000 deposit in my checking account (creating a demand deposit). How much is credited in the reserve account of my bank?
Does the Treasury do the crediting in the reserve account, or is it the fed?
Ramanan,
You are completely missing my point.
The point was about stock/flow consistency, which I know is one of your most valued ideas, and which is the only reason I made the point.
I said effectively that it is not stock/flow consistent to allege at the macro level that consumption comes “out of” previously accumulated wealth – for a generic/global/or closed macro economy.
I’ll redo it using your final example of a closed economy:
C is not spent “out of” either S or the accumulation of S (wealth before marked to market).
C is spent “out of” [C + S + T]; i.e. it is spent “out of” current income, before subtracting consumption obviously.
In other words, C is not spent “out of” the residual that is left after C. You can see the absurdity of such a construction.
And that holds whether you are talking about the residual from current income (saving), or the residual from all prior income (wealth).
I’m quite familiar with the type of consumption function you’ve noted.
That equation is essentially a regression equation of consumption against two variables – current disposable income and wealth.
You must understand the difference between a behavioural regression equation and the actual flows at the macro level.
That equation DOESN’T mean that “the consumption function is both OUT OF income and WEALTH IN THE PREVIOUS PERIOD”, as you put it.
It means that the consumption amount is equivalent to the amount determined by such a behavioural equation. There is a big difference between a behavioural regression equation as an explanation for aggregate demand and the actual flow of funds that is required to facilitate that aggregate demand.
That equation does not allocate consumption to flows and stocks at the macro level. It can’t, because to do so would be stock/flow inconsistent. Macro closed economy consumption obviously comes “out of” current income. Expressed as C + S + T, that income already includes a specific allocation for consumption.
JKH,
I understood your point right from the first comment because the terminology such as consumption out of wealth seems to be mixing stocks and flows. However, it is not. Just because a flow depends on stocks does not mean it is stock flow inconsistent.
What I have written is nowhere close to being absurd, I am afraid.
Consumption during a period depends on the household expected income and accumulated wealth. It is a behavioral conjecture not some regression.
Now, I could give some references to the people who actually invented the stock-flow consistent modeling but that is not the best way to proceed. But trust me, my knowledge is fully from their work and what I am writing is not from my own imagination!
Lets go back to basics. Let us divide historic time into various periods. Consumption functions such as C = alpha x Y are firstly themselves incorrect, because they assume perfect foresight. So one should be talking of expected income or the previous period income etc.
The fact that stocks and flows depend on each other has completely confounded economists.
Maybe “out of” is not the best terminology. Nonetheless, there is nothing wrong with the consumption function I wrote and I repeat, it is not a regression equation – it is a behavioral hypothesis. It IS stock flow consistent.
Let me give an analogy.
The observed fiscal policy of a government depends on the public debt. In other words, government tighten fiscal policy if the public debt is above a level. This can be represented as
G = G(-1) + Beta x (Public Debt(-1)/GDP(-1) – 60%)
The left hand side is a flow – ‘pure’ government expenditures (which excludes interest payments) and the right hand side contains a stock – the public debt.
The problem with a consumption function which includes only the present period income is this. Every period, the household sector saves some fraction of the national income. Imagine the consequences of such an assumption. The public debt keeps rising forever relative to the gdp. You may want to include growth (which you have talked of in the context of net external debt) but one gets a big number.
I perfectly understand what you are trying to say. How can consumption depend on something which is a residual itself. In other words, if it starts depending on the residual, then its not residual by definition and things along those lines.
Maybe just a point about “out of” ? (as you yourself say)
Fed Up:
a. $1000
b. Treasury through its account with the feds.
Also Americans consume a lot because of capital gains, and capital gains are not flows – they are a part of a revaluation matrix and adds to the stock of wealth. Its not too incorrect to say the Americans consume out of capital gains. They make take more credit instead of realizing the capital gains. They make take credit independent of this and end up spending more than there income. In that case, Americans cannot be said to be spending out of income, because that is less than their expenditures.
Also since the household sector is represented as one unit, I do not see why this sector cannot be said to have consumed from the wealth. Old people have interest income but they also consume from accumulated wealth because they have a finite lifetime.
Ramanan,
Whether it’s a regression equation or a behavioural conjecture from thin air or a behavioural equation constructed with the benefit of regression analysis (which is what I said it was) or an equation from God doesn’t concern me.
It’s got nothing to do with stock/flow reconciliation in a closed economy at the macro level.
“Maybe just a point about “out of”? (as you yourself say)”
That’s entirely the point. That’s why I kept putting it in quotations. Don’t know why you argued against it for 90 per cent of what you wrote and then conceded it.
Point me to just one of your stock flow gurus who used that particular language – the link please.
“But trust me, my knowledge is fully from their work and what I am writing is not from my own imagination!”
Words mean something. The words are yours. No offence, but “trusting you” has nothing to do with it.
“Its not too incorrect to say the Americans consume out of capital gains.”
I already said that the current account deficit can be interpreted as consuming from wealth, because it reduces net wealth of the US at the margin. But that’s an example of an open economy, where the US is one sector in a US/non-US global economy. At that level, the global economy is the closed one where the non-US sector runs a current account surplus and the global total can’t/doesn’t consume “out of” wealth.
The same holds for any sector break down which admits openings where a particular unit or sector may have negative saving. Clearly that’s the case with the capital gain wealth effect as it affects consumption by certain households and the household sector as a whole, etc. etc.
JKH,
Monetary Economics – by Wynne Godley and Marc Lavoie you see this in page 71.
Part of the whole story so you may wonder what is happening exactly, but the language is there. Its the simplest model with the government sector, firms and households and not much complication.
They also define alpha2 as “Propensity to consume out of past wealth”
Whether the usage “out of” is right or wrong is not the best point to debate – economics is about behaviour, not just accounting identities. Physical sciences are consistent with Mathematics but one can construct zillions of theories consistent with Mathematics. In a similar way, one can think of hundreds and thousands of ways economies behave consistent with national accounting. However, it is suggestive and it doesn’t prevent one from making assumptions x, y, z. Great discoveries have come out of conjecturing something and following it with analysis.
You may not want to believe in the second term of the consumption function – that’s your perspective. However, you have to note that the simpler consumption function is also a behavioral hypothesis!
Now after going through this exercise, your initial point that “the wealth effect is already taken into account in the MPC assumption” doesn’t hold. To capture the wealth effect, you need another parameter. That is where the debate started didn’t it ?
Perhaps you think that consuming out of wealth is a wrong usage because it seems to erode wealth whereas in general household wealth increases. Not necessarily – the household sector may be said to be consuming from the previously accumulated wealth but the saving in the period can add to the wealth such that the wealth doesn’t erode.
Similarly, the household sector wealth can be increasing even while running current account deficits because of various things.
And at a global level, net financial wealth is zero. And similarly income. That doesn’t mean nobody is consuming.
Ramanan,
They’re obviously explaining a multiplier example.
So think of a Billy-like simplified model with autonomous G of 100 and a propensity to consumer of .8, and just saving apart from that.
So you get a Billy-like propagation of consumption of 80, 64, etc. following the injection.
And you get final cumulative saving of 100 and consumption of 400 when the process reaches equilibrium.
As far as I can tell, what they’re saying is that the initial G produces initial G’ saving of 100 (i.e. net financial assets) and that the propensity to consume takes over until equilibrium is reached with cumulative consumption finally in balance with the initial NFA injection. That looks like standard multiplier stuff to me. I don’t have a problem with any of it.
The multiplier process is obviously an out of equilibrium one, taking a number of iterations to resolve. I will grant that in this case of the multiplier mechanism, the consumption that eventually falls out of the “forced saving” injection (NFA) takes time to resolve itself. Consumption is spread over a multi-period process, which itself is a forced timing construct of the multiplier mechanism. I also have no problem with that.
But again this overlooks the larger point, which is that the multiplier example of an autonomous government injection is framed in what is essentially a sector financial balances model. So the case you make for consumption “out of wealth” in this example depends on that sector breakdown.
I’ve already said that sector consumptions “out of wealth” are acknowledged – like the basic case of the US current account deficit in the context of a closed global economy.
Importantly, in the example you cite, G’ (non government) is NOT a closed macro economy in concept. It’s about the most open economy you can think of. It is a sector in the economy G u G’.
In the closed economy G u G’, sector financial balances sum to zero by definition.
And in the closed economy G u G’, S = I for all income periods, and C is taken out of current income – not from current S or prior S.
MOREOVER, these macro equivalences hold even within the multi-period process of consumption resolution via the multiplier.
Accordingly, there is no consumption “out of” wealth at the macro closed level, which remains my point.
“Now after going through this exercise, your initial point that “the wealth effect is already taken into account in the MPC assumption” doesn’t hold.”
Obviously, the MPC formulation in the example you cite above explicitly takes it into account. But you can’t claim or know that the MPC functions in Bill’s examples didn’t take it into account, merely because he didn’t state what the functions were explicitly. How do you know what the functional formulation of the MPC functions was in Bill’s problem? You don’t. Just because the function wasn’t stated explicitly, you assume the wealth effect was excluded from the underlying functions. Why?
JKH,
In the way you have explained, maybe doing it in an excel sheet, one needs to calculate consumption according to assumptions made about the behaviour. So it comes down to putting in a formula for the consumption, while making extra care that this is not inconsistent with accounting identities which need to be satisfied by definitions.
The basic mutliplier model stops at the first step or a few steps and don’t go into what happens in the long term. So what I have quoted is not a simple multiplier stuff.
Now you ask how I know whether the function I prefer is different from what’s in Q5 and you have to just look at the section Consumption and Saving where it has been explicitly stated.
Or perhaps, you are arguing that there shouldn’t be an additional term in the consumption function. That itself an assumption and there is nothing to prevent one from assuming otherwise. It is perfectly stock-flow consistent. It has additional advantages of explaining many things and at a practical level, the CBO should learn it.
The reason I have taken it up is it is a wonderful term. The Keynesian function on the other hand implies that the public debt to gdp ratio rises without a limit or stabilizes to a high value very different from what is seen in real economies. Try it to believe it.
It also helps to understand when processes can get to unsustainable level especially in the context of open economies. If a basic model itself has the public debt rising relative to gdp without a limit, its difficult to understand what “sustainability” means.
Ramanan,
“you have to just look at the section Consumption and Saving where it has been explicitly stated”
This may not be satisfactory to you, Ramanan, but my working assumption there is that since that is the standard MPC expression, the income coefficient approximates the combined effect of the two separate coefficients in the other expression, assuming both expressions are reasonably accurate. The income coefficient therefore is different in the two different equations.
vjk said: “Fed Up:
a. $1000
b. Treasury through its account with the feds.”
Does it have to be $1,000? In the private sector, I’m thinking a new demand deposit from say a mortgage has only a 10% reserve requirement (or even less?).
For b, I think I need some more information on how the federal gov’t and the fed interact. Thanks!
Fed Up,
VJK has it completely right. You are confusing balances in the bank’s reserve account ($1000 in your example, as VJK said, since that was the $ value of the transaction) with the minimum qty of balances the bank is required to hold in its reserve account ($100 in your example if the required reserve ratio is 10%).
Best,
Scott
Ramanan,
You are free come up with all sorts of functions that determine C. There is a lot of literature that relates optimal levels of consumption to the size of your portfolio, expected future wage income, and personal time preference. It’s fair to assume that all these are drivers of C, even at the sectoral level. By writing them down as linear functions with coefficients that you estimate from data, you are using a very simple calibrated model — I would even say a log-linearized model — which is extremely common.
But I don’t understand why you *need* to derive the consumption flow this way in order to maintain stock-flow consistency, or why wealth/income would be infinite if you didn’t.
I suspect you are either not marking W to market, and/or not properly discounting.
Embedded in W is an expectation of a stream of future savings, or more appropriately, future investment, that justifies the growth from W to (1+r)W in between periods. That applies at least loosely even if you save in the form of a collectible that you expect to appreciate at r% — others must be willing to save larger amounts in the form of that collectible in order to create a market for it. If you save in the form of an asset, then there is an expectation of an ongoing stream of earnings that justify the price of the asset, etc. I’m not saying the actual price is just a geometric sum.
But you don’t have a relationship of the form W[n] = (1+r)W[n-1] + S[n] at the aggregate level, and when properly discounted, W/Y is not going to go to infinity or zero.
An individual household may have such a relationship over very short time scales (between re-pricings of W), but if “too many” try to save, then they will find that W is re-priced. If too few try to save, aggregate W may increase or decrease.
You can only say that rW[n-1] = S[n] when S[n] is exactly the expected level of savings demanded in a world with constant multiples and perfect future knowledge. In that case, W[n] = (1+r)W[n-1] = W[n-1] + S[n], but the causality is not a simple case of a flow during a period adding to a stock, but rather a savings requirement being met. If too many tried to save, then W might plunge in value, and if too few, then W might either increase or decrease, depending on your other assumptions.
vjk, Scott Fullwiler, or anyone else, so when the gov’t spends, it ALWAYS (emphasis) creates a demand deposit and credits the reserve account by the same amount (1 to 1). Is that correct?
Is it the same when private debt is created? Thanks!
Fed Up,
The Treasury spends by debiting its own account at the Fed, resulting in a credit to the reserve account of the spending recipient’s bank. The bank in turn credits the account of the recipient. Yes, it’s 1 to 1.
When private debt is created, assuming you are talking about a bank making the loan, the loan creates a deposit. So, the asset and liability sides of the bank’s balance sheet also increase, 1 to 1. But, in this case, there is no change to the bank’s reserve account. Aggregate reserves only change when there is a change to the Fed’s balance sheet (e.g., a change to the Treasury’s account).
Best,
Scott
On a kind-of-related note to Fed Up’s question, if the Fed go ahead with QE2 they will effectively just be swapping bonds for cash at the reserve accounts of the commercial banks – is that correct?
If so, would that not mean the banks would now have an abundance of cash in their reserves, not earning any interest (unlike the bonds), and so would just want to swap the cash back for bonds again? And if that’s the case, is there any evidence that this is what happened after the first round of QE?
Thanks.
RSJ,
abababab (long time no c)! Where had you been ? Vacationing ? Welcome back.
Yes I agree. One can come up with anything. However, what I said was not something like whether function x is correct and y is wrong etc.
What I meant was that the simple Keynesian function is a bit incomplete in the sense that it implies that every period there is saving and if you watch out for the wealth in this model, you will find that the wealth keeps increasing relative to the gdp. In the real world wealth may keep increasing for some time and then go down and do all kinds of fluctuation. It however doesn’t keep increasing forever relative to the gdp and the public debt (a mirror of private sector wealth) is ‘low’ for most countries. Such as 40%, 60%, 80% etc.
Be careful about writing terms such as (1+r)W. The interest paid is income and not a stock. The opening stock is W(-1). Saving is added to the opening stock to get the stock at the end of the period. And you have to make assumptions about whether interest income is consumed or not etc and you seem to be assuming that it is not.
Okay here is why in the absence of the wealth term, the public debt keeps increasing. In the simple closed economy model with the wealth term, the public debt (which is a mirror of the private sector wealth) converges to (1-alpha1)/alpha2 x G (1-θ)/θ. Here θ is the tax rate and alpha1 and alpha2 are the two propensities. You can see that if alpha2 is zero, the public debt doesn’t converge.
What I am emphasising is that the story that income once saved and never consumed again doesn’t look so plausible. Unlike the Ricardian Equivalence story, people quickly consume stuff. This is because if they only consume a part of the income and save the rest to never consume again, the wealth keeps increasing forever – finding themselves with a higher wealth, consumers will quickly spend it. The wealth term captures this effect which the Keynesian consumption function doesn’t.
vp:
If so, would that not mean the banks would now have an abundance of cash in their reserves, not earning any interest (unlike the bonds), and so would just want to swap the cash back for bonds again?
Banks, per se, are not the major holders of government securities of long maturity. So, most likely, during QE1, the major contributors to cash growth on banks’ reserve accounts were non-banks. Assuming banks did contribute substantially to their reserve account growth by selling their own government security holdings for whatever reason, they could try and re-buy securities, on the open market, from other non-government holders. However, such action would be rather impotent with respect to reducing cumulative reserves since the grand total of cash in the system would remain the same (as RSJ pointed out “elsewhere”), cash will only change the hands.
A more interesting question is: what motivation, behaviorally speaking, the non-government QE1 players had when they decided to sell their government bond holdings ?
[Banks do get paid interest, currently, for holding extra reserves ]
For vjk, Scott Fullwiler, or anyone else, so ALL debt whether private or gov’t has three “components”, the loan, the deposit, and the reserve balance.
If gov’t debt has a 1 to 1 deposit and reserve balance and a 10% reserve requirement for the deposit, then a $1,000 deposit also has a $1,000 reserve balance and $900 is excess.
If private debt has a 1 to 0 deposit and reserve balance and a 10% reserve requirement for the deposit, then a $1,000 deposit has a $0 reserve balance and $100 in “deficit reserves”.
In the gov’t debt case, the fed funds rate wants to go lower.
In the private debt case, the fed funds rate wants to go higher.
Is all that correct?
Plus, I don’t understand why in the gov’t debt case, the gov’t does not need to just put $100 into the reserve balance instead of $1,000.
*****
And, “The Treasury spends by debiting its own account at the Fed, …”
Where does the Treasury get its “funds” from? Thanks!
Good to see you, too, R! I’ve been a bit swamped with r/l.
Yeah, so that’s why I think there is something wrong with the model 🙂 Every period all the income is spent on consumption or investment. No income is not spent, so I don’t see the issue here …
See, that’s what I’m arguing against, and it may be the error in the model.
Asset prices are _not_ _independent_ of the amount that households save, and the relationship is not additive in nature. Your model is missing a constraint that express the savings demanded by households given the level of assets and return required.
An individual household can save any amount without this affecting the price of assets, but the household sector as a whole cannot.
You can only add W to S when the savings that are demanded are exactly equal to the savings that are realized. The level of savings demand will be embedded in the asset values, so S_demanded = f(r,W). In a single asset case, that would be something like S = rW.
When that condition is violated, then what happens will depend heavily on the details of your model, but generally speaking W falls to some smaller level, W’, so that S = rW’, but you can also have movements in r as well, i.e. r can decrease to r’ so that S = r’W with W unchanged.
It will be some combination of the two, but a good model should assume that asset price values will bear the brunt of adjustment rather an a lowering of the cost of capital (and a subsequent increase in multiples).
This could be why you see problems with unrealistic W/Y ratios in the model, in that they correspond to an unrealistic asset pricing assumption.
Yes and no. All private debt has two components: The lender’s asset (corresponding to a liability for the borrower), and the borrower’s newly created deposits (an asset for the borrower, a liability for the lender). That’s a feature of double-entry bookkeeping, so that’s always true for loans that are well described by double-entry bookkeeping. (The sovereign is special, because it (and only it) can create deposits without incurring a liability of its own, thereby obviating the need for a corresponding bond.)
In addition, it is considered prudent to require that all deposit-taking institutions hold reserves against the deposits they have taken on (and that insurance companies hold reserves against their policies, etc.). It is also considered prudent to require that banks maintain a certain percentage of equity relative to their balance sheet.
Now, the latter two rules don’t actually relate to the mechanics of lending – it is perfectly possible to operate a banking system in which neither of them is enforced (the development of the shadow banking system over the last couple of business cycles was largely due to a desire to get around these particular rules). A system without those rules won’t be very stable (as the shadow banking system of the previous decade demonstrated, to our considerable discomfort), but that doesn’t mean that you can’t run the system without them.
More or less. It is usually unhelpful to think in terms of reserve requirements under a modern central banking system. It is much more useful to think in terms of rediscount rates (the price that the central bank takes for providing liquidity) and solidity requirements (the bank must remain below a certain ratio of liabilities to equity), since the central bank will usually provide unlimited liquidity to its member banks (as long as they are willing to pay the discount window’s interest rate). Thinking in terms of reserve requirements and open market operations is a legacy from premodern private reserve banks who did not have the ability to provide unlimited access to the discount window (and in fact a rather strong case can be made that relying on open market operations to achieve the central bank’s target rate offers grossly inferior precision in monetary policy, compared to using the discount window).
The government doesn’t “put $100 into the reserve balance.” The government puts $ 1.000 into the bank’s deposits, and the bank figures out how much (minimum $ 100) it wants to put into the reserve balance.
It creates them out of thin air. That’s what legal tender laws do for you.
– Jake
JakeS said: “The government doesn’t “put $100 into the reserve balance.” The government puts $ 1.000 into the bank’s deposits, and the bank figures out how much (minimum $ 100) it wants to put into the reserve balance.”
vjk and Scott Fullwiler both told me it is $1,000.
Scott Fullwiler said: “The Treasury spends by debiting its own account at the Fed, resulting in a credit to the reserve account of the spending recipient’s bank. The bank in turn credits the account of the recipient. Yes, it’s 1 to 1.”
Oh, right.
We’re using “reserve balance” differently.
They simply mean the bank’s bank account with the Fed. The $ 1000 is the bank’s new deposits with the central bank. From your $ 100 comment, I thought you were talking about fulfilling the reserve requirements. Sorry, my bad.
– Jake