Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – January 8, 2011 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
If the national government stopped issuing public debt then its deficit spending would be more expansionary than if it matched the deficits with new debt issues.
The answer is False.
The mainstream macroeconomic textbooks all have a chapter on fiscal policy (and it is often written in the context of the so-called IS-LM model but not always).
The chapters always introduces the so-called Government Budget Constraint that alleges that governments have to “finance” all spending either through taxation; debt-issuance; or money creation. The writer fails to understand that government spending is performed in the same way irrespective of the accompanying monetary operations.
They claim that money creation (borrowing from central bank) is inflationary while the latter (private bond sales) is less so. These conclusions are based on their erroneous claim that “money creation” adds more to aggregate demand than bond sales, because the latter forces up interest rates which crowd out some private spending.
All these claims are without foundation in a fiat monetary system and an understanding of the banking operations that occur when governments spend and issue debt helps to show why.
So what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a budget deficit without issuing debt?
Like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.
The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made. Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet). Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.
This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management. The aim of the central bank is to “hit” a target interest rate and so it has to ensure that competitive forces in the interbank market do not compromise that target.
When there are excess reserves there is downward pressure on the overnight interest rate (as banks scurry to seek interest-earning opportunities), the central bank then has to sell government bonds to the banks to soak the excess up and maintain liquidity at a level consistent with the target. Some central banks offer a return on overnight reserves which reduces the need to sell debt as a liquidity management operation.
There is no sense that these debt sales have anything to do with “financing” government net spending. The sales are a monetary operation aimed at interest-rate maintenance. So M1 (deposits in the non-government sector) rise as a result of the deficit without a corresponding increase in liabilities. It is this result that leads to the conclusion that that deficits increase net financial assets in the non-government sector.
What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.
The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).
There is no difference to the impact of the deficits on net worth in the non-government sector.
Mainstream economists would say that by draining the reserves, the central bank has reduced the ability of banks to lend which then, via the money multiplier, expands the money supply.
However, the reality is that:
- Building bank reserves does not increase the ability of the banks to lend.
- The money multiplier process so loved by the mainstream does not describe the way in which banks make loans.
- Inflation is caused by aggregate demand growing faster than real output capacity. The reserve position of the banks is not functionally related with that process.
So the banks are able to create as much credit as they can find credit-worthy customers to hold irrespective of the operations that accompany government net spending.
This doesn’t lead to the conclusion that deficits do not carry an inflation risk. All components of aggregate demand carry an inflation risk if they become excessive, which can only be defined in terms of the relation between spending and productive capacity.
It is totally fallacious to think that private placement of debt reduces the inflation risk. It does not.
You may wish to read the following blogs for more information:
- Why history matters
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- The complacent students sit and listen to some of that
- Saturday Quiz – February 27, 2010 – answers and discussion
Question 2:
Non-government sector net worth does not change when the government issues debt which exactly matches ($-for-$) the increase in net public spending.
The answer is True.
This answer is complementary to that provided for Question 1 and relies on the same understanding of reserve operations. So within a fiat monetary system we need to understand the banking operations that occur when governments spend and issue debt. That understanding allows us to appreciate what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a budget deficit without issuing debt?
Like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.
The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made. Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet). Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.
This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management as explained in the asnwer to Question 1. But at this stage, M1 (deposits in the non-government sector) rise as a result of the deficit without a corresponding increase in liabilities. In other words, budget deficits increase net financial assets in the non-government sector.
What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.
The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).
There is no difference to the impact of the deficits on net worth in the non-government sector.
You may wish to read the following blogs for more information:
- Why history matters
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- The complacent students sit and listen to some of that
- Saturday Quiz – February 27, 2010 – answers and discussion
Question 3:
For the wage share in GDP to remain constant, wages have to keep pace with the growth in labour productivity.
The answer is False.
The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.
To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.
Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.
The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.
So the wage bill = W.L
The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.
Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:
LP = GDP/L
so it tells us what real output (GDP) each labour unit that is added to production produces on average.
We can also define another term that is regularly used in the media – the real wage – which is the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).
We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.
Macroeconomics is hard to learn because it involves these abstract variables that are never observed – like the price level, like “the interest rate” etc. They are just stylisations of the general tendency of all the different prices and interest rates.
Now the nominal wage (W) – that is paid by employers to workers is determined in the labour market – by the contract of employment between the worker and the employer. The price level (P) is determined in the goods market – by the interaction of total supply of output and aggregate demand for that output although there are complex models of firm price setting that use cost-plus mark-up formulas with demand just determining volume sold. We shouldn’t get into those debates here.
The inflation rate is just the continuous growth in the price level (P). A once-off adjustment in the price level is not considered by economists to constitute inflation.
So the real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).
We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.
Nominal GDP ($GDP) can be written as P.GDP, where the P values the real physical output.
Now if you put of these concepts together you get an interesting framework. To help you follow the logic here are the terms developed and be careful not to confuse $GDP (nominal) with GDP (real):
- Wage share = (W.L)/$GDP
- Nominal GDP: $GDP = P.GDP
- Labour productivity: LP = GDP/L
- Real wage: w = W/P
By substituting the expression for Nominal GDP into the wage share measure we get:
Wage share = (W.L)/P.GDP
In this area of economics, we often look for alternative way to write this expression – it maintains the equivalence (that is, obeys all the rules of algebra) but presents the expression (in this case the wage share) in a different “view”.
So we can write as an equivalent:
Wage share – (W/P).(L/GDP)
Now if you note that (L/GDP) is the inverse (reciprocal) of the labour productivity term (GDP/L). We can use another rule of algebra (reversing the invert and multiply rule) to rewrite this expression again in a more interpretable fashion.
So an equivalent but more convenient measure of the wage share is:
Wage share = (W/P)/(GDP/L) – that is, the real wage (W/P) divided by labour productivity (GDP/L).
I won’t show this but I could also express this in growth terms such that if the growth in the real wage equals labour productivity growth the wage share is constant. The algebra is simple but we have done enough of that already.
That journey might have seemed difficult to non-economists (or those not well-versed in algebra) but it produces a very easy to understand formula for the wage share.
Two other points to note. The wage share is also equivalent to the real unit labour cost (RULC) measures that Treasuries and central banks use to describe trends in costs within the economy. Please read my blog – Saturday Quiz – May 15, 2010 – answers and discussion – for more discussion on this point.
So it becomes obvious that the correct statement is that the real wage has to keep pace with productivity growth for the wage share to remain constant. If the nominal wage (W) and the price level (P) are growing at the pace the real wage is constant. And if the real wage is growing at the same rate as labour productivity, then both terms in the wage share ratio are equal and so the wage share is constant.
The wage share was constant for a long time during the Post Second World period and this constancy was so marked that Kaldor (the Cambridge economist) termed it one of the great “stylised” facts. So real wages grew in line with productivity growth which was the source of increasing living standards for workers.
The productivity growth provided the “room” in the distribution system for workers to enjoy a greater command over real production and thus higher living standards without threatening inflation.
Since the mid-1980s, the neo-liberal assault on workers’ rights (trade union attacks; deregulation; privatisation; persistently high unemployment) has seen this nexus between real wages and labour productivity growth broken. So while real wages have been stagnant or growing modestly, this growth has been dwarfed by labour productivity growth.
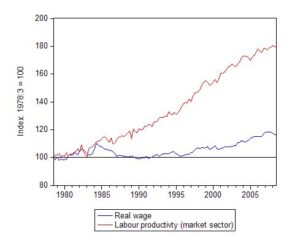
In this blog – The origins of the economic crisis – I provided these graphs. First, the movement real wages and labour productivity since 1979. Both series are indexed to 100 as at the September quarter 1978. So by September 2008, the real wage index had climbed to 116.7 (that is, around 15 per cent growth in just over 12 years) but the labour productivity index was 179.1.
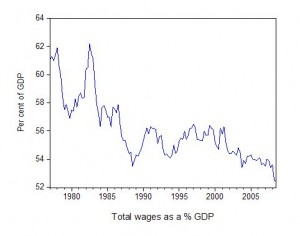
This suggests from our discussion that the wage share should have fallen. That is what the next graph depicts – it shows how far the wage share has fallen in Australia over the last two decades. The trend has been common across the globe during the neo-liberal years and is one of the pre-conditions that explain our current economic crisis.
The following blogs may be of further interest to you:
Question 4:
If net exports are contributing to economic growth, then the national government has the room to run a budget surplus without impeding that growth.
The answer is Maybe.
First, you need to understand the basic relationship between the sectoral flows and the balances that are derived from them. The flows are derived from the National Accounting relationship between aggregate spending and income. So:
(1) Y = C + I + G + (X – M)
where Y is GDP (income), C is consumption spending, I is investment spending, G is government spending, X is exports and M is imports (so X – M = net exports).
Another perspective on the national income accounting is to note that households can use total income (Y) for the following uses:
(2) Y = C + S + T
where S is total saving and T is total taxation (the other variables are as previously defined).
You than then bring the two perspectives together (because they are both just “views” of Y) to write:
(3) C + S + T = Y = C + I + G + (X – M)
You can then drop the C (common on both sides) and you get:
(4) S + T = I + G + (X – M)
Then you can convert this into the familiar sectoral balances accounting relations which allow us to understand the influence of fiscal policy over private sector indebtedness.
So we can re-arrange Equation (4) to get the accounting identity for the three sectoral balances – private domestic, government budget and external:
(S – I) = (G – T) + (X – M)
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.
Another way of saying this is that total private savings (S) is equal to private investment (I) plus the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
Thus, when an external deficit (X – M < 0) and public surplus (G – T < 0) coincide, there must be a private deficit. While private spending can persist for a time under these conditions using the net savings of the external sector, the private sector becomes increasingly indebted in the process.
Second, you then have to appreciate the relative sizes of these balances to answer the question correctly.
Consider the following Table which depicts three cases – two that define a state of macroeconomic equilibrium (where aggregate demand equals income and firms have no incentive to change output) and one (Case 2) where the economy is in a disequilibrium state and income changes would occur.
Note that in the equilibrium cases, the (S – I) = (G – T) + (X – M) whereas in the disequilibrium case (S – I) > (G – T) + (X – M) meaning that aggregate demand is falling and a spending gap is opening up. Firms respond to that gap by decreasing output and income and this brings about an adjustment in the balances until they are back in equality.
So in Case 1, assume that the private domestic sector desires to save 2 per cent of GDP overall (spend less than they earn) and the external sector is running a surplus equal to 4 per cent of GDP.
In that case, aggregate demand will be unchanged if the government runs a surplus of 2 per cent of GDP (noting a negative sign on the government balance means T > G).
In this situation, the surplus does not undermine economic growth because the injections into the spending stream (NX) are exactly offset by the leakages in the form of the private saving and the budget surplus. This is the Norwegian situation.
In Case 2, we hypothesise that the private domestic sector now wants to save 6 per cent of GDP and they translate this intention into action by cutting back consumption (and perhaps investment) spending.
Clearly, aggregate demand now falls by 4 per cent of GDP and if the government tried to maintain that surplus of 2 per cent of GDP, the spending gap would start driving GDP downwards.
The falling income would not only reduce the capacity of the private sector to save but would also push the budget balance towards deficit via the automatic stabilisers. It would also push the external surplus up as imports fell. Eventually the income adjustments would restore the balances but with lower GDP overall.
So Case 2 is a not a position of rest – or steady growth. It is one where the government sector (for a given net exports position) is undermining the changing intentions of the private sector to increase their overall saving.
In Case 3, you see the result of the government sector accommodating that rising desire to save by the private sector by running a deficit of 2 per cent of GDP.
So the injections into the spending stream are 4 per cent from NX and 2 per cent from the deficit which exactly offset the desire of the private sector to save 6 per cent of GDP. At that point, the system would be in rest.
This is a highly stylised example and you could tell a myriad of stories that would be different in description but none that could alter the basic point.
If the drain on spending outweighs the injections into the spending stream then GDP falls (or growth is reduced).
So even though an external surplus is being run, the desired budget balance still depends on the saving desires of the private domestic sector. Under some situations, these desires could require a deficit even with an external surplus.
So the best answer is Maybe – that is, the result is conditional on the behaviour of the private domestic sector.
You may wish to read the following blogs for more information:
- Back to basics – aggregate demand drives output
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
- Barnaby, better to walk before we run
- Saturday Quiz – June 19, 2010 – answers and discussion
Question 5: Premium question
A central bank can control bank lending while maintaining its target monetary policy rate by increasing the price that it charges commercial banks for reserves.
The answer is False.
The facts are as follows. First, central banks will always provided enough reserve balances to the commercial banks at a price it sets using a combination of overdraft/discounting facilities and open market operations.
Second, if the central bank didn’t provide the reserves necessary to match the growth in deposits in the commercial banking system then the payments system would grind to a halt and there would be significant hikes in the interbank rate of interest and a wedge between it and the policy (target) rate – meaning the central bank’s policy stance becomes compromised.
Third, any reserve requirements within this context while legally enforceable (via fines etc) do not constrain the commercial bank credit creation capacity. Central bank reserves (the accounts the commercial banks keep with the central bank) are not used to make loans. They only function to facilitate the payments system (apart from satisfying any reserve requirements).
Fourth, banks make loans to credit-worthy borrowers and these loans create deposits. If the commercial bank in question is unable to get the reserves necessary to meet the requirements from other sources (other banks) then the central bank has to provide them. But the process of gaining the necessary reserves is a separate and subsequent bank operation to the deposit creation (via the loan).
Fifth, if there were too many reserves in the system (relative to the banks’ desired levels to facilitate the payments system and the required reserves then competition in the interbank (overnight) market would drive the interest rate down. This competition would be driven by banks holding surplus reserves (to their requirements) trying to lend them overnight. The opposite would happen if there were too few reserves supplied by the central bank. Then the chase for overnight funds would drive rates up.
In both cases the central bank would lose control of its current policy rate as the divergence between it and the interbank rate widened. This divergence can snake between the rate that the central bank pays on excess reserves (this rate varies between countries and overtime but before the crisis was zero in Japan and the US) and the penalty rate that the central bank seeks for providing the commercial banks access to the overdraft/discount facility.
So the aim of the central bank is to issue just as many reserves that are required for the law and the banks’ own desires.
Now the question seeks to link the penalty rate that the central bank charges for providing reserves to the banks and the central bank’s target rate. The wider the spread between these rates the more difficult does it become for the central bank to ensure the quantity of reserves is appropriate for maintaining its target (policy) rate.
Where this spread is narrow, central banks “hit” their target rate each day more precisely than when the spread is wider.
So if the central bank really wanted to put the screws on commercial bank lending via increasing the penalty rate, it would have to be prepared to lift its target rate in close correspondence. In other words, its monetary policy stance becomes beholden to the discount window settings.
The best answer was false because the central bank cannot operate with wide divergences between the penalty rate and the target rate and it is likely that the former would have to rise significantly to choke private bank credit creation.
You might like to read this blogs for further information:

“Central bank reserves (the accounts the commercial banks keep with the central bank) are not used to make loans.”
Someone once told me there wasn’t anything as a central bank reserve. They just said it was an asset of the bank/commercial bank.
I tried to explain that there are central bank reserves (I actually call them one-day gov’t debt in disguise if the gov’t won’t let the central bank fail). Central bank reserves are a medium of exchange inside the banking system covered by the fed only and are an asset of the commercial bank and a liability of the fed.
Can someone clear this up for me? Thanks!
Also, where do central bank reserves come from?
1) gov’t spends/cuts taxes. Someone’s demand deposit account gets “marked up” and the commercial bank’s reserve account gets “marked up” with central bank reserves 1 to 1.
2) Someone takes currency to a bank for deposit, and the bank then exchanges the currency 1 to 1 for central bank reserves.
3) The fed creates central bank reserves whenever it wants to.
Are those correct? Any others?
“Second, if the central bank didn’t provide the reserves necessary to match the growth in deposits in the commercial banking system then the payments system would grind to a halt and there would be significant hikes in the interbank rate of interest and a wedge between it and the policy (target) rate – meaning the central bank’s policy stance becomes compromised.”
Can the fed lower the reserve requirement and/or reclassify deposits into another category where the reserve requirement is lower or zero?
Fed Up,
Yes the Fed can change reserve requirements up or down but it hasn’t done that in the last 20 years or so (not sure of the dates) and yes it can impose requirements on some deposits and not on others. In the US, time deposits do not attract reserve requirements, for example.
Most countries do not change reserve requirements, and the only two countries I can think of that do are China and India. Instead of changing RR, they just change interest rates.
The connection between tax cuts and reserves is indirect. If – for a given government spending – taxes paid turn out to be lower, issuance of Treasuries is higher.
Yes, when someone exchange currency notes for deposits, banks’ reserves position changes.
The statement “The Fed creates central bank reserves whenever it wants to” can be misleading in many ways. Let us first assume that the central bank has a corridor system of implementing monetary policy as opposed to a floor system. It has no control over the reserves. For example, if the central bank purchases foreign currency, the reserves increase at first, but the central bank immediately does a “sterilization” operation.
Having said that, the Fed can purchase any asset such as government bonds, MBS etc and create reserves. It can pay interest on reserves and change the interest paid on reserves when it wants to change the Fed Funds target.
Bill,
re question number 1
On the effects of abandoning the existing Government Budget Constraints(GBC) on economic expansion.
I believe that action to fund the deficits with new, debt-free money creation by the government would be more expansionary, that is result in higher GDP and employment growth in the future, than if the deficits were debt-funded.
This is simply because of the lack of an interest payment in future years being taken from the economy just for the privilege of having the debt-funded economic activity.
IOW, if we don’t issue the government debts too cover the deficits, then in future years the tax payments that would be drawn by the government to pay the interest would be available to go to more productive(employment and ecomic expansion) purposes.
This seems to be the findings of Japanese economist Dr. Kaoru Yamaguchi who modeled a transition from a debt-money system that included the GBR to a debt-free monetary system where the government was enabled to add new money to the economy, as provided in the annual budgeting process, up to the amount needed to meet potential GDP growth.
Dr. Yamaguchi’s paper titled: On the Liquidation of Government Debt Under a Debt-Free Monetary System is available here:
http://bs.doshisha.ac.jp/download/files/activity10/discussion/DBS-10-01.pdf
The findings actually say that a long-term benefit of the transition to a debt-free money system is the achievement of real GDP-potential(full-employment) without inflation or deflation, while eliminating the national debt of the government.
Congressman Dennis Kucinich has introduced legislation, the National Emergency Employment Defense (NEED) Act of 2010 that proposes just such a reform to the nation’s money system. It is available here.
http://kucinich.house.gov/UploadedFiles/NEED_ACT.pdf
Anyway, that’s what I believe, based on what I’ve read, but I could be wrong.
Thanks, Bill.
Fed up, reserves are entries on the central bank’s spreadsheet that serve to settle interbank accounts. Accounting-wise, reserves are cb liabilities and bank assets. The reside in the various reserve accounts that those institutions that are members of the interbank system hold there.
Reserves are for settlement of accounts only. Final settlement of transactions in the economy occur in two ways, 1) exchange of currency, and 2) transfer of reserves between accounts in the interbank system.
Currency and reserves are interchangeable. Banks exchange reserves in their reserve accounts with the cb for currency for their cash vaults, and vice versa.
Reserves are created when the Treasury spends into the economy by crediting bank accounts. The cb supplies the reserves to the Treasury account to settle these transaction. Through settlement, the reserves from the Treasury account pass into the reserve accounts of various banks. The reserves go back into the Treasury account when taxes are paid by check, and the checks drawn on deposit accounts at the banks are settled.
If you think of it in terms of accounting for transactions as they are settled in the interback system, it is pretty simple. If all transactions were settled by cash changing hands, the interbank system would not be needed. But since that is unwieldy, most of it is accomplished electronically now as numbers shift around on spreadsheets.
joebhed, you may be interested in this proposal in the UK too. (I am not endorsing it and have criticized it in the comment section there).
http://www.positivemoney.org.uk/
Tom,
It seems to me that you are living in some pre-Mayan framework in which zero is not a number and therefore setting a price of zero does not correspond to price setting.
For the rest of us, setting a price of zero is the same as setting a price of 1, or 2, etc. 🙂
That’s true, of course, RSJ, but the cb setting the overnight price of risk-free money to zero and maintaining it there is effectively a declaration to the market that the market will set the price of money in terms risk independently of cb policy intervention – which is what I meant to convey, perhaps poorly. While setting the overnight rate to zero is rate setting of a sort, it is quite different from variable rate setting for policy reasons, and it lets the market set rates based exclusively on credit standards and economic conditions.
Tom,
Thanks for the link.
Ben Dyson of Positive Money is a friend and we both presented at the American Monetary Institute’s Monetary Reform Conference last Fall in Chicago.
I went to the PM site(quickly) to look for your comments but couldn’t find them.
Is there a link to your comment thread?
Thanks.
Here’s the comment:
Tom Hickey
January 9, 2011 · 6:09 am
Lots of good ideas but the idea that the MPC woud have control over money creation is even more insane than the system in place. The idea of interest rates set by a small group of technocrats is bad enough, but to put quantity in their hands compounds the problem. It is basically a command system rather than a market based system and it is elitist rather than democratic.
Change that aspect of the proposal and you have some good ideas that move the debate forward. But a putting a small group of unelected and unaccountable technocrats in charge is a non-starter.
http://www.positivemoney.org.uk/how-it-works/
Thanks for the comments everyone.