Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – October 8, 2011 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
Some “Occupy Wall Street” protesters are demanding that bank lending should be more closely regulated to ensure that all bank loans were backed by reserves held at the bank. However, this would unnecessarily reduce the capacity of the banks to lend.
The answer is False.
In a “fractional reserve” banking system of the type the US runs (which is really one of the relics that remains from the gold standard/convertible currency era that ended in 1971), the banks have to retain a certain percentage (10 per cent currently in the US) of deposits as reserves with the central bank. You can read about the fractional reserve system from the Federal Point page maintained by the FRNY.
Where confusion as to the role of reserve requirements begins is when you open a mainstream economics textbooks and “learn” that the fractional reserve requirements provide the capacity through which the private banks can create money. The whole myth about the money multiplier is embedded in this erroneous conceptualisation of banking operations.
The FRNY educational material also perpetuates this myth. They say:
If the reserve requirement is 10%, for example, a bank that receives a $100 deposit may lend out $90 of that deposit. If the borrower then writes a check to someone who deposits the $90, the bank receiving that deposit can lend out $81. As the process continues, the banking system can expand the initial deposit of $100 into a maximum of $1,000 of money ($100+$90+81+$72.90+…=$1,000). In contrast, with a 20% reserve requirement, the banking system would be able to expand the initial $100 deposit into a maximum of $500 ($100+$80+$64+$51.20+…=$500). Thus, higher reserve requirements should result in reduced money creation and, in turn, in reduced economic activity.
This is not an accurate description of the way the banking system actually operates and the FRNY (for example) clearly knows their representation is stylised and inaccurate. Later in the same document they they qualify their depiction to the point of rendering the last paragraph irrelevant. After some minor technical points about which deposits count to the requirements, they say this:
Furthermore, the Federal Reserve operates in a way that permits banks to acquire the reserves they need to meet their requirements from the money market, so long as they are willing to pay the prevailing price (the federal funds rate) for borrowed reserves. Consequently, reserve requirements currently play a relatively limited role in money creation in the United States.
In other words, the required reserves play no role in the credit creation process.
The actual operations of the monetary system are described in this way. Banks seek to attract credit-worthy customers to which they can loan funds to and thereby make profit. What constitutes credit-worthiness varies over the business cycle and so lending standards become more lax at boom times as banks chase market share (this is one of Minsky’s drivers).
These loans are made independent of the banks’ reserve positions. Depending on the way the central bank accounts for commercial bank reserves, the latter will then seek funds to ensure they have the required reserves in the relevant accounting period. They can borrow from each other in the interbank market but if the system overall is short of reserves these “horizontal” transactions will not add the required reserves. In these cases, the bank will sell bonds back to the central bank or borrow outright through the device called the “discount window”.
At the individual bank level, certainly the “price of reserves” will play some role in the credit department’s decision to loan funds. But the reserve position per se will not matter. So as long as the margin between the return on the loan and the rate they would have to borrow from the central bank through the discount window is sufficient, the bank will lend.
So the idea that reserve balances are required initially to “finance” bank balance sheet expansion via rising excess reserves is inapplicable. A bank’s ability to expand its balance sheet is not constrained by the quantity of reserves it holds or any fractional reserve requirements. The bank expands its balance sheet by lending. Loans create deposits which are then backed by reserves after the fact. The process of extending loans (credit) which creates new bank liabilities is unrelated to the reserve position of the bank.
The major insight is that any balance sheet expansion which leaves a bank short of the required reserves may affect the return it can expect on the loan as a consequence of the “penalty” rate the central bank might exact through the discount window. But it will never impede the bank’s capacity to effect the loan in the first place.
The money multiplier myth leads students to think that as the central bank can control the monetary base then it can control the money supply. Further, given that inflation is allegedly the result of the money supply growing too fast then the blame is sheeted home to the “government” (the central bank in this case).
The reality is that the reserve requirements that might be in place at any point in time do not provide the central bank with a capacity to control the money supply.
So would it matter if reserve requirements were 100 per cent? In this blog – 100-percent reserve banking and state banks – I discuss the concept of a 100 per cent reserve system which is favoured by many conservatives who believe that the fractional reserve credit creation process is inevitably inflationary.
There are clearly an array of configurations of a 100 per cent reserve system in terms of what might count as reserves. For example, the system might require the reserves to be kept as gold. In the old “Giro” or “100 percent reserve” banking system which operated by people depositing “specie” (gold or silver) which then gave them access to bank notes issued up to the value of the assets deposited. Bank notes were then issued in a fixed rate against the specie and so the money supply could not increase without new specie being discovered.
Another option might be that all reserves should be in the form of government bonds, which would be virtually identical (in the sense of “fiat creations”) to the present system of central bank reserves.
While all these issues are interesting to explore in their own right, the question does not relate to these system requirements of this type. It was obvious that the question maintained a role for central bank (which would be unnecessary in a 100-per cent reserve system based on gold, for example.
It is also assumed that the reserves are of the form of current current central bank reserves with the only change being they should equal 100 per cent of deposits.
We also avoid complications like what deposits have to be backed by reserves and assume all deposits have to so backed.
In the current system, the the central bank ensures there are enough reserves to meet the needs generated by commercial bank deposit growth (that is, lending). As noted above, the required reserve ratio has no direct influence on credit growth. So it wouldn’t matter if the required reserves were 10 per cent, 0 per cent or 100 per cent.
In a fiat currency system, commercial banks require no reserves to expand credit. Even if the required reserves were 100 per cent, then with no other change in institutional structure or regulations, the central bank would still have to supply the reserves in line with deposit growth.
Now I noted that the central bank might be able to influence the behaviour of banks by imposing a penalty on the provision of reserves. It certainly can do that. As a monopolist, the central bank can set the price and supply whatever volume is required to the commercial banks.
But the price it sets will have implications for its ability to maintain the current policy interest rate which we consider in Question 3.
The central bank maintains its policy rate via open market operations. What really happens when an open market purchase (for example) is made is that the central bank adds reserves to the banking system. This will drive the interest rate down if the new reserve position is above the minimum desired by the banks. If the central bank wants to maintain control of the interest rate then it has to eliminate any efforts by the commercial banks in the overnight interbank market to eliminate excess reserves.
One way it can do this is by selling bonds back to the banks. The same would work in reverse if it was to try to contract the money supply (a la money multiplier logic) by selling government bonds.
The point is that the central bank cannot control the money supply in this way (or any other way) except to price the reserves at a level that might temper bank lending.
So if it set a price of reserves above the current policy rate (as a penalty) then the policy rate would lose traction for reasons explained in the answer to Question 3.
The fact is that it is endogenous changes in the money supply (driven by bank credit creation) that lead to changes in the monetary base (as the central bank adds or subtracts reserves to ensure the “price” of reserves is maintained at its policy-desired level). Exactly the opposite to that depicted in the mainstream money multiplier model.
The other fact is that the money supply is endogenously generated by the horizontal credit (leveraging) activities conducted by banks, firms, investors etc – the central bank is not involved at this level of activity.
You might like to read these blogs for further information:
- Lending is capital- not reserve-constrained
- Oh no … Bernanke is loose and those greenbacks are everywhere
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- 100-percent reserve banking and state banks
- Money multiplier and other myths
Question 2:
Taxation creates unemployment.
The answer is True.
First, to clear the ground we state clearly that a sovereign government is the monopoly issuer of the currency and is never revenue-constrained. So the question is not about the tax revenue per se but rather the role taxes play in the monetary system. A sovereign government never has to “obey” the constraints that the private sector always has to obey.
The foundation of many mainstream macroeconomic arguments is the fallacious analogy they draw between the budget of a household/corporation and the government budget. However, there is no parallel between the household (for example) which is clearly revenue-constrained because it uses the currency in issue and the national government, which is the issuer of that same currency.
The choice (and constraint) sets facing a household and a sovereign government are not alike in any way, except that both can only buy what is available for sale. After that point, there is no similarity or analogy that can be exploited.
Of-course, the evolution in the 1960s of the literature on the so-called government budget constraint (GBC), was part of a deliberate strategy to argue that the microeconomic constraint facing the individual applied to a national government as well. Accordingly, they claimed that while the individual had to “finance” its spending and choose between competing spending opportunities, the same constraints applied to the national government. This provided the conservatives who hated public activity and were advocating small government, with the ammunition it needed.
So the government can always spend if there are goods and services available for purchase, which may include idle labour resources. This is not the same thing as saying the government can always spend without concern for other dimensions in the aggregate economy.
For example, if the economy was at full capacity and the government tried to undertake a major nation building exercise then it might hit inflationary problems – it would have to compete at market prices for resources and bid them away from their existing uses.
In those circumstances, the government may – if it thought it was politically reasonable to build the infrastructure – quell demand for those resources elsewhere – that is, create some unemployment. How? By increasing taxes.
So to answer the question correctly, you need to understand the role that taxes play in a fiat currency system.
In a fiat monetary system the currency has no intrinsic worth. Further the government has no intrinsic financial constraint. Once we realise that government spending is not revenue-constrained then we have to analyse the functions of taxation in a different light. The starting point of this new understanding is that taxation functions to promote offers from private individuals to government of goods and services in return for the necessary funds to extinguish the tax liabilities.
In this way, it is clear that the imposition of taxes creates unemployment (people seeking paid work) in the non-government sector and allows a transfer of real goods and services from the non-government to the government sector, which in turn, facilitates the government’s economic and social program.
The crucial point is that the funds necessary to pay the tax liabilities are provided to the non-government sector by government spending. Accordingly, government spending provides the paid work which eliminates the unemployment created by the taxes.
So it is now possible to see why mass unemployment arises. It is the introduction of State Money (government taxing and spending) into a non-monetary economics that raises the spectre of involuntary unemployment. As a matter of accounting, for aggregate output to be sold, total spending must equal total income (whether actual income generated in production is fully spent or not each period). Involuntary unemployment is idle labour offered for sale with no buyers at current prices (wages).
Unemployment occurs when the private sector, in aggregate, desires to earn the monetary unit of account, but doesn’t desire to spend all it earns, other things equal. As a result, involuntary inventory accumulation among sellers of goods and services translates into decreased output and employment. In this situation, nominal (or real) wage cuts per se do not clear the labour market, unless those cuts somehow eliminate the private sector desire to net save, and thereby increase spending.
The purpose of State Money is for the government to move real resources from private to public domain. It does so by first levying a tax, which creates a notional demand for its currency of issue. To obtain funds needed to pay taxes and net save, non-government agents offer real goods and services for sale in exchange for the needed units of the currency. This includes, of-course, the offer of labour by the unemployed. The obvious conclusion is that unemployment occurs when net government spending is too low to accommodate the need to pay taxes and the desire to net save.
This analysis also sets the limits on government spending. It is clear that government spending has to be sufficient to allow taxes to be paid. In addition, net government spending is required to meet the private desire to save (accumulate net financial assets). From the previous paragraph it is also clear that if the Government doesn’t spend enough to cover taxes and desire to save the manifestation of this deficiency will be unemployment.
Keynesians have used the term demand-deficient unemployment. In our conception, the basis of this deficiency is at all times inadequate net government spending, given the private spending decisions in force at any particular time.
So the answer should now be obvious. If the economy is to fulfill its political mandate it must be able to transfer real productive resources from the private sector to the public sector. Taxation is the vehicle that a sovereign government uses to “free up resources” so that it can use them itself. But taxation has nothing to do with “funding” of the government spending.
To understand how taxes are used to attenuate demand please read this blog – Functional finance and modern monetary theory.
The following blogs may be of further interest to you:
- The budget deficits will increase taxation!
- Will we really pay higher taxes?
- A modern monetary theory lullaby
- Functional finance and modern monetary theory
- Deficit spending 101 – Part 1
- Deficit spending 101 – Part 2
- Deficit spending 101 – Part 3
Question 3:
Assume a nation is running an external surplus equivalent to 2 per cent of GDP and the private domestic sector is currently saving overall 1 per cent of GDP. In this situation, the government must be running:
(a) A budget deficit equal to 1 per cent of GDP.
(b) A budget surplus equal to 1 per cent of GDP.
(c) A budget deficit equal to 3 per cent of GDP.
(d) A budget surplus equal to 3 per cent of GDP.
The answer is Option (d) – A budget surplus equal to 1 per cent of GDP.
This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.
We know that from an accounting sense, if the external sector overall is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the accounting rules.
The important point is to understand what behaviour and economic adjustments drive these outcomes.
So here is the accounting (again). The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X – M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I – S) + (G – T) + (X – M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
- The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
- The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
- The Current Account balance (X – M) – positive if in surplus, negative if in deficit.
These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
So what economic behaviour might lead to the outcome specified in the question?
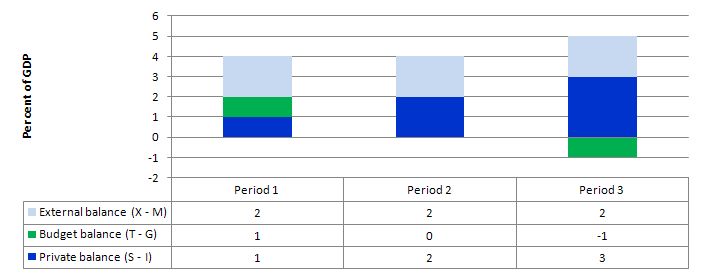
The following graph shows three situations where the external sector is in surplus of 2 per cent of GDP and the private domestic balance is in surplus of varying proportions of GDP (note I have written the budget balance as (T – G).
In Period 1, the private domestic balance is in surplus (1 per cent of GDP) and the budget is also in surplus (1 per cent of GDP). The net injection to demand from the external sector (equivalent to 2 per cent of GDP) is sufficient to “fund” the private saving drain from expenditure without compromising economic growth. The growth in income would also allow the budget to be in surplus (via tax revenue).
In Period 2, the rise in private domestic saving drains extra aggregate demand and necessitates a more expansionary position from the government (relative to Period 1), which in this case manifests as a balanced public budget,’
Period 3, relates to the data presented in the question – an external surplus of 2 per cent of GDP and private domestic saving equal to 3 per cent of GDP. Now the demand injection from the external sector is being more than offset by the demand drain from private domestic saving. The income adjustments that would occur in this economy would then push the budget into deficit of 1 per cent of GDP.
The movements in income associated with the spending and revenue patterns will ensure these balances arise.
The general rule is that the government budget deficit (surplus) will always equal the non-government surplus (deficit).
So if there is an external surplus that is greater than private domestic sector saving (a surplus) then there will always be a budget surplus. Equally, the higher the private saving is relative to the external surplus, the larger the budget deficit.
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 4:
Start from a situation where the external balance is the equivalent of 2 per cent of GDP and the budget surplus is 2 per cent. If the budget balance stays constant and the external balance rises to the equivalent of 4 per cent of GDP then:
(a) National income rises and the private surplus moves from 4 per cent of GDP to 6 per cent of GDP.
(b) National income remains unchanged and the private surplus moves from 4 per cent of GDP to 6 per cent of GDP.
(c) National income falls and the private surplus moves from 4 per cent of GDP to 6 per cent of GDP.
(d) National income rises and the private surplus moves from 0 per cent of GDP to 2 per cent of GDP.
(e) National income remains unchanged and the private surplus moves from 0 per cent of GDP to 2 per cent of GDP
(f) National income falls and the private surplus moves from 0 per cent of GDP to 2 per cent of GDP.
The answer is Option (d) National income rises and the private surplus moves from 0 per cent of GDP to 2 per cent of GDP.
Please refer to the explanation in Question 3 for the conceptual material required to understand this question and answer.
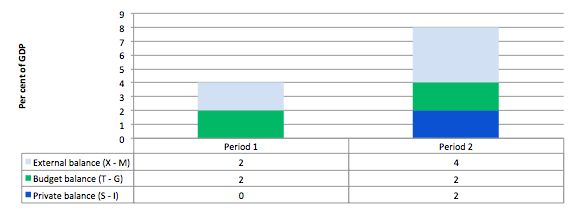
Consider the following graph and accompanying table which depicts two periods outlined in the question.
In Period 1, with an external surplus of 2 per cent of GDP and a budget surplus of 2 per cent of GDP the private domestic balance is zero. The demand injection from the external sector is exactly offset by the demand drain (the fiscal drag) coming from the budget balance and so the private sector can neither net save or spend more than they earn.
In Period 2, with the external sector adding more to demand now – surplus equal to 4 per cent of GDP and the budget balance unchanged (this is stylised – in the real world the budget will certainly change), there is a stimulus to spending and national income would rise.
The rising national income also provides the capacity for the private sector to save overall and so they can now save 2 per cent of GDP.
The fiscal drag is overwhelmed by the rising net exports.
This is a highly stylised example and you could tell a myriad of stories that would be different in description but none that could alter the basic point.
If the drain on spending (from the public sector) is more than offset by an external demand injection, then GDP rises and the private sector overall saving increases.
If the drain on spending from the budget outweighs the external injections into the spending stream then GDP falls (or growth is reduced) and the overall private balance would fall into deficit.
You may wish to read the following blogs for more information:
- Back to basics – aggregate demand drives output
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
- Barnaby, better to walk before we run
- Saturday Quiz – June 19, 2010 – answers and discussion
Premium Question 5:
Assume a nation’s public debt to GDP ratio rises to 100 per cent. The central bank keeps its nominal interest rate at zero and a zero inflation rate persists. Under these circumstances fiscal austerity packages that create recession can still reduce the public debt to GDP ratio, as long as the primary surplus to GDP ratio is greater than the negative GDP growth rate.
The answer is True.
First, some background.
While Modern Monetary Theory (MMT) places no particular importance in the public debt to GDP ratio for a sovereign government, given that insolvency is not an issue, the mainstream debate is dominated by the concept.
The unnecessary practice of fiat currency-issuing governments of issuing public debt $-for-$ to match public net spending (deficits) ensures that the debt levels will rise when there are deficits.
Rising deficits usually mean declining economic activity (especially if there is no evidence of accelerating inflation) which suggests that the debt/GDP ratio may be rising because the denominator is also likely to be falling or rising below trend.
Further, historical experience tells us that when economic growth resumes after a major recession, during which the public debt ratio can rise sharply, the latter always declines again.
It is this endogenous nature of the ratio that suggests it is far more important to focus on the underlying economic problems which the public debt ratio just mirrors.
However, mainstream economics starts with the analogy between the household and the sovereign government such that any excess in government spending over taxation receipts has to be “financed” in two ways: (a) by borrowing from the public; and/or (b) by “printing money”.
This basic analogy is flawed at its most elemental level. The household must work out the financing before it can spend. The household cannot spend first. The government can spend first and ultimately does not have to worry about financing such expenditure.
However, in mainstream framework for analysing these so-called “financing” choices is called the government budget constraint (GBC). The GBC says that the budget deficit in year t is equal to the change in government debt over year t plus the change in high powered money over year t. So in mathematical terms it is written as:
Which you can read in English as saying that Budget deficit = Government spending + Government interest payments – Tax receipts must equal (be “financed” by) a change in Bonds (B) and/or a change in high powered money (H). The triangle sign (delta) is just shorthand for the change in a variable.
However, this is merely an accounting statement. In a stock-flow consistent macroeconomics, this statement will always hold. That is, it has to be true if all the transactions between the government and non-government sector have been corrected added and subtracted.
So in terms of MMT, the previous equation is just an ex post accounting identity that has to be true by definition and has not real economic importance.
But for the mainstream economist, the equation represents an ex ante (before the fact) financial constraint that the government is bound by. The difference between these two conceptions is very significant and the second (mainstream) interpretation cannot be correct if governments issue fiat currency (unless they place voluntary constraints on themselves to act as if it is).
Further, in mainstream economics, money creation is erroneously depicted as the government asking the central bank to buy treasury bonds which the central bank in return then prints money. The government then spends this money. This is called debt monetisation and you can find out why this is typically not a viable option for a central bank by reading the Deficits 101 suite – Deficit spending 101 – Part 1 – Deficit spending 101 – Part 2 – Deficit spending 101 – Part 3.
Anyway, the mainstream claims that if governments increase the money growth rate (they erroneously call this “printing money”) the extra spending will cause accelerating inflation because there will be “too much money chasing too few goods”! Of-course, we know that proposition to be generally preposterous because economies that are constrained by deficient demand (defined as demand below the full employment level) respond to nominal demand increases by expanding real output rather than prices. There is an extensive literature pointing to this result.
So when governments are expanding deficits to offset a collapse in private spending, there is plenty of spare capacity available to ensure output rather than inflation increases.
But not to be daunted by the “facts”, the mainstream claim that because inflation is inevitable if “printing money” occurs, it is unwise to use this option to “finance” net public spending.
Hence they say as a better (but still poor) solution, governments should use debt issuance to “finance” their deficits. They also claim this is a poor option because in the short-term it is alleged to increase interest rates and in the longer-term is results in higher future tax rates because the debt has to be “paid back”.
Neither proposition bears scrutiny – you can read these blogs – Will we really pay higher taxes? and Will we really pay higher interest rates? – for further discussion on these points.
A primary budget balance is the difference between government spending (excluding interest rate servicing) and taxation revenue.
The standard mainstream framework, which even the so-called progressives (deficit-doves) use, focuses on the ratio of debt to GDP rather than the level of debt per se. The following equation captures the approach:
So the change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP.
The real interest rate is the difference between the nominal interest rate and the inflation rate.
The standard formula above can easily demonstrate that a nation running a primary deficit can reduce its public debt ratio over time as long as economic growth is strong enough.
Furthermore, depending on contributions from the external sector, a nation running a deficit will more likely create the conditions for a reduction in the public debt ratio than a nation that introduces an austerity plan aimed at running primary surpluses.
But it is also true that an austerity package which damages real growth can also reduce the public debt ratio.
That is the focus of this question which assumes:
- Current public debt to GDP ratio is 100 per cent = 1.
- Nominal interest rate (i) and the inflation rate (p) remain constant and zero, which means the real interest rate (r = i – p) = 0.
The following Table shows three cases:
- Case A – primary budget surplus to GDP ratio exceeds the negative GDP growth rate.
- Case B – primary budget to GDP ratio is equal to the negative GDP growth rate.
- Case C – primary budget to GDP ratio is less than the negative GDP growth rate.
The case in question is Case A.
In Case A, the primary budget surplus to GDP ratio (2 per cent – note it is presented as a negative figure given that the budget balance is presented as [G – T]) exceeds the negative GDP growth rate (-1 per cent). In this case, the debt ratio falls by the difference (given the real interest rate is zero).
As long as the primary surplus as a per cent of GDP is exactly equal to the negative GDP growth rate (Case B), there can be no reduction in the public debt ratio. This is because what is being added proportionately to the numerator of the ratio is also being added to the denominator.
Under Case C where the primary budget surplus is 2 per cent and the contraction in real GDP is 3 percent for the debt ratio rises by the difference.
How likely is it that Case A would occur in the real world when the government was pursuing such a fiscal path? Answer: unlikely.
First, fiscal austerity will probably push the GDP growth rate further into negative territory which, other things equal, pushes the public debt ratio up. Why? The budget balance is endogenous (that is, depends on private activity levels) because of the importance of the automatic stabilisers.
As GDP contracts, tax revenue falls and welfare outlays rise. It is highly likely that the government would not succeed in achieving a budget surplus under these circumstances.
So as GDP growth declines further, the automatic stabilisers will push the balance result towards (and into after a time) deficit, which, given the borrowing rules that governments volunatarily enforce on themselves, also pushed the public debt ratio up.
So austerity packages, quite apart from their highly destructive impacts on real standards of living and social standards, typically fail to reduce public debt ratios and usually increase them.
So even if you were a conservative and erroneously believed that high public debt ratios were the devil’s work, it would be foolish (counter-productive) to impose fiscal austerity on a nation as a way of addressing your paranoia. Better to grit your teeth and advocate higher deficits and higher real GDP growth.
That strategy would also be the only one advocated by MMT.

Bill,
From a fellow bill I thank you for the tremendous time and effort you put into this wonderful blog. The scales fall from my eyes daily.
Q3, “The answer is Option (d) – A budget surplus equal to 1 per cent of GDP.”
Isn’t that option (b)?
Hi Bill! I love your blog and am learning a lot (but be patient with me cause I’m still learnin’). I have bit of a problem with your explanation about why it is true that taxation creates unemployment. I think I see the point that, as a matter of accounting, the introduction of State Money creates unemployment, but it seems to me that you are using the word “unemployment” in a very specific sense. For the average reader, what seems confusing is that while the national accounts require logically that the economy operates in the fashion you describe, we are well aware that many countries with high taxes have had full employment. This fits, of course, neatly with your statement that unemployment occurs when net government spending is too low to accommodate the need to pay taxes and the desire to net save. Now, if I understand it correctly, MMT says that there is no “pass-through” of taxes: taxes are collected to regulate demand, not to finance spending per se. And yet, many governments still operating under gold-standard principles, as if the public spending were based on the collection of fixed amounts of money from citizens, have been able to sufficiently stimulate the economy to have full employment. When that occurs (as a result of ideological preference), accumulated tax revenues have been spent (presumably more efficiently) by the public sector as employment-generating public investments. So, in that case, it does not seem accurate to say that taxes reduce aggregate demand (although that is obviously true in one sense) since in “taxing and spending” the government has not reduced actual investment in economy, and actually increased national income by investing more efficiently than the private sector would have done if left alone. Now, I understand that the key for full employment is the public spending not the accumulation of tax revenue, but perhaps MMTers could reformulate how they express their observations on the role of taxation in the economy and its relationship to unemployment?
Bill,
This is difficult to understand because you have mixed the terminology and then to make the math work you define a positive as a negative and a negative as a positive.
You call this:
(I – S) + (G – T) + (X – M) = 0
the “sectoral balances view of the national accounts.” Then you confuse the terminology:
You refer to the Private Domestic Balance as Savings, but savings is a part of the Private Domestic Balance. Then, to maintain your terminology, you define a positive Private Domestic Balance as a negative.
You call the Government Balance the budget deficit. To make your terminology work, you define a positive Government Balance as a negative. A budget deficit is what you have when the Government Balance IS negative.
You call the third sector balance the Current Account balance, but you refer to it all the time as the external balance (see the tables) or external sector. Since you said that you are defining “sectoral balances,” you should stick to naming it the External Balance. Then word your description as follows:
That is the three balances have to sum to zero. The sectoral balances derived are:
• The Private Domestic Balance: (I – S).
• The Government Balance: (G – T).
• The External Balance: (X – M).
Going further, change
“In Period 1, the private domestic balance is in surplus (1 per cent of GDP) and the budget is also in surplus (1 per cent of GDP). The net injection to demand from the external sector (equivalent to 2 per cent of GDP) is sufficient…”
to read
“In Period 1, there is a savings surplus of 1 per cent of GDP and a budget surplus of 1 per cent of GDP. The net injection to demand from the external sector of 2 per cent of GDP is sufficient …”
The reason is that a savings surplus of 1 per cent equals a Private Domestic Balance of negative 1 per cent, and a budget surplus of 1 per cent equals a Government Balance of negative 1 per cent. (-1 + -1 + 2 = 0)
I leave it to you to reword the rest, including the tables (and don’t forget to put minus signs on the numbers in the table).
In reference to my earlier post, this:
You call the Government Balance the budget deficit. To make your terminology work, you define a positive Government Balance as a negative. A budget deficit is what you have when the Government Balance IS negative.
Should read:
You call the Government Balance the budget deficit. To make your terminology work, you define a positive Government Balance as a negative. A budget deficit is what you have when the Government Balance is positive.