Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – October 15, 2011 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
We are told that a country is running a small current account deficit and that the private domestic sector is saving overall. However, we cannot tell what the government budget balance will be as a percentage of GDP until we know the relative magnitudes of the other two balances.
The answer is False.
This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.
Refreshing the balances – we know that from an accounting sense, if the external sector overall is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the accounting rules.
The important point is to understand what behaviour and economic adjustments drive these outcomes.
The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X – M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I – S) + (G – T) + (X – M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
- The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
- The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
- The Current Account balance (X – M) – positive if in surplus, negative if in deficit.
These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
So what economic behaviour might lead to the outcome specified in the question?
If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down. The reference to a “small” external deficit was to place doubt in your mind. In fact, it doesn’t matter how large the external deficit is for this question.
Assume, now that the private domestic sector (households and firms) seeks to increase its overall saving (that is, spend less than it earns) and is successful in doing so. Consistent with this aspiration, households may cut back on consumption spending and save more out of disposable income. The immediate impact is that aggregate demand will fall and inventories will start to increase beyond the desired level of the firms.
The firms will soon react to the increased inventory holding costs and will start to cut back production. How quickly this happens depends on a number of factors including the pace and magnitude of the initial demand contraction. But if the households persist in trying to save more and consumption continues to lag, then soon enough the economy starts to contract – output, employment and income all fall.
The initial contraction in consumption multiplies through the expenditure system as workers who are laid off also lose income and their spending declines. This leads to further contractions.
The declining income leads to a number of consequences. Net exports improve as imports fall (less income) but the question clearly assumes that the external sector remains in deficit. Total saving actually starts to decline as income falls as does induced consumption.
So the initial discretionary decline in consumption is supplemented by the induced consumption falls driven by the multiplier process.
The decline in income then stifles firms’ investment plans – they become pessimistic of the chances of realising the output derived from augmented capacity and so aggregate demand plunges further. Both these effects push the private domestic balance further towards and eventually into surplus
With the economy in decline, tax revenue falls and welfare payments rise which push the public budget balance towards and eventually into deficit via the automatic stabilisers.
If the private sector persists in trying to net save then the contracting income will clearly push the budget into deficit.
So we would have an external deficit, a private domestic surplus and a budget deficit.
There will always be a budget deficit at any national income level, if the private domestic sector is succeessfully spending less than it earns and the external sector is in deficit.
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 2:
The private sector is wealthier if the government matches its deficit spending with bond issues relative to if the government just spent without issuing bonds (that is, instructed the central bank to credit bank accounts).
The answer is False.
This answer relies on an understanding the banking operations that occur when governments spend and issue debt within a fiat monetary system. That understanding allows us to appreciate what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a budget deficit without issuing debt?
In this situation, like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.
The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made. Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet). Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.
This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management. The aim of the central bank is to “hit” a target interest rate and so it has to ensure that competitive forces in the interbank market do not compromise that target.
When there are excess reserves there is downward pressure on the overnight interest rate (as banks scurry to seek interest-earning opportunities), the central bank then has to sell government bonds to the banks to soak the excess up and maintain liquidity at a level consistent with the target. Some central banks offer a return on overnight reserves which reduces the need to sell debt as a liquidity management operation.
What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.
The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).
There is no difference to the impact of the deficits on net worth in the non-government sector.
Mainstream economists would say that by draining the reserves, the central bank has reduced the ability of banks to lend which then, via the money multiplier, expands the money supply.
However, the reality is that:
- Building bank reserves does not increase the ability of the banks to lend.
- The money multiplier process so loved by the mainstream does not describe the way in which banks make loans.
- Inflation is caused by aggregate demand growing faster than real output capacity. The reserve position of the banks is not functionally related with that process.
So the banks are able to create as much credit as they can find credit-worthy customers to hold irrespective of the operations that accompany government net spending.
This doesn’t lead to the conclusion that deficits do not carry an inflation risk. All components of aggregate demand carry an inflation risk if they become excessive, which can only be defined in terms of the relation between spending and productive capacity.
It is totally fallacious to think that private placement of debt reduces the inflation risk. It does not.
You may wish to read the following blogs for more information:
- Why history matters
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- The complacent students sit and listen to some of that
- Saturday Quiz – February 27, 2010 – answers and discussion
Question 3:
Modern Monetary Theory (MMT) explains how central banks sell bonds to drain excess bank reserves in order to maintain their given interest rate setting. We know that the same outcome can be achieved by paying interest to the commercial banks on the same reserves. Ignoring any reserve requirements, this means that there is no need for government (via the central bank) to issue debt when it net spends.
The answer is False.
Mainstream macroeconomics textbooks tells students that monetary policy describes the processes by which the central bank determines “the total amount of money in existence or to alter that amount”.
In Mankiw’s Principles of Economics (Chapter 27 First Edition) he say that the central bank has “two related jobs”. The first is to “regulate the banks and ensure the health of the financial system” and the second “and more important job”:
… is to control the quantity of money that is made available to the economy, called the money supply. Decisions by policymakers concerning the money supply constitute monetary policy (emphasis in original).
How does the mainstream see the central bank accomplishing this task? Mankiw says:
Fed’s primary tool is open-market operations – the purchase and sale of U.S government bonds … If the FOMC decides to increase the money supply, the Fed creates dollars and uses them buy government bonds from the public in the nation’s bond markets. After the purchase, these dollars are in the hands of the public. Thus an open market purchase of bonds by the Fed increases the money supply. Conversely, if the FOMC decides to decrease the money supply, the Fed sells government bonds from its portfolio to the public in the nation’s bond markets. After the sale, the dollars it receives for the bonds are out of the hands of the public. Thus an open market sale of bonds by the Fed decreases the money supply.
This description of the way the central bank interacts with the banking system and the wider economy is false. The reality is that monetary policy is focused on determining the value of a short-term interest rate. Central banks cannot control the money supply. To some extent these ideas were a residual of the commodity money systems where the central bank could clearly control the stock of gold, for example. But in a credit money system, this ability to control the stock of “money” is undermined by the demand for credit.
The theory of endogenous money is central to the horizontal analysis in Modern Monetary Theory (MMT). When we talk about endogenous money we are referring to the outcomes that are arrived at after market participants respond to their own market prospects and central bank policy settings and make decisions about the liquid assets they will hold (deposits) and new liquid assets they will seek (loans).
The essential idea is that the “money supply” in an “entrepreneurial economy” is demand-determined – as the demand for credit expands so does the money supply.
As credit is repaid the money supply shrinks. These flows are going on all the time and the stock measure we choose to call the money supply, say M3 (Currency plus bank current deposits of the private non-bank sector plus all other bank deposits from the private non-bank sector) is just an arbitrary reflection of the credit circuit.
So the supply of money is determined endogenously by the level of GDP, which means it is a dynamic (rather than a static) concept.
Central banks clearly do not determine the volume of deposits held each day. These arise from decisions by commercial banks to make loans. The central bank can determine the price of “money” by setting the interest rate on bank reserves. Further expanding the monetary base (bank reserves) as we have argued in recent blogs – Building bank reserves will not expand credit and Building bank reserves is not inflationary – does not lead to an expansion of credit.
With this background in mind, the question is specifically about the dynamics of bank reserves which are used to satisfy any imposed reserve requirements and facilitate the payments system. These dynamics have a direct bearing on monetary policy settings. Given that the dynamics of the reserves can undermine the desired monetary policy stance (as summarised by the policy interest rate setting), the central banks have to engage in liquidity management operations.
What are these liquidity management operations?
Well you first need to appreciate what reserve balances are.
The New York Federal Reserve Bank’s paper – Divorcing Money from Monetary Policy said that:
… reserve balances are used to make interbank payments; thus, they serve as the final form of settlement for a vast array of transactions. The quantity of reserves needed for payment purposes typically far exceeds the quantity consistent with the central bank’s desired interest rate. As a result, central banks must perform a balancing act, drastically increasing the supply of reserves during the day for payment purposes through the provision of daylight reserves (also called daylight credit) and then shrinking the supply back at the end of the day to be consistent with the desired market interest rate.
So the central bank must ensure that all private cheques (that are funded) clear and other interbank transactions occur smoothly as part of its role of maintaining financial stability. But, equally, it must also maintain the bank reserves in aggregate at a level that is consistent with its target policy setting given the relationship between the two.
So operating factors link the level of reserves to the monetary policy setting under certain circumstances. These circumstances require that the return on “excess” reserves held by the banks is below the monetary policy target rate. In addition to setting a lending rate (discount rate), the central bank also sets a support rate which is paid on commercial bank reserves held by the central bank.
Many countries (such as Australia and Canada) maintain a default return on surplus reserve accounts (for example, the Reserve Bank of Australia pays a default return equal to 25 basis points less than the overnight rate on surplus Exchange Settlement accounts). Other countries like the US and Japan have historically offered a zero return on reserves which means persistent excess liquidity would drive the short-term interest rate to zero.
The support rate effectively becomes the interest-rate floor for the economy. If the short-run or operational target interest rate, which represents the current monetary policy stance, is set by the central bank between the discount and support rate. This effectively creates a corridor or a spread within which the short-term interest rates can fluctuate with liquidity variability. It is this spread that the central bank manages in its daily operations.
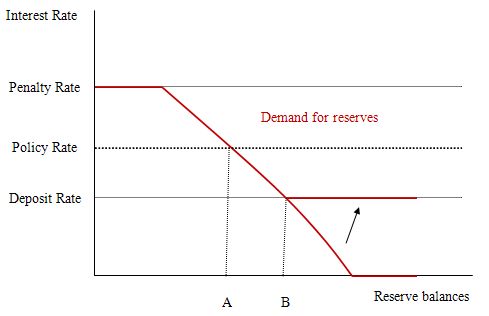
So the issue then becomes – at what level should the support rate be set? To answer that question, I reproduce a version of the diagram from the FRBNY paper which outlined a simple model of the way in which reserves are manipulated by the central bank as part of its liquidity management operations designed to implement a specific monetary policy target (policy interest rate setting).
I describe the FRBNY model in detail in the blog – Understanding central bank operations so I won’t repeat that explanation.
The penalty rate is the rate the central bank charges for loans to banks to cover shortages of reserves. If the interbank rate is at the penalty rate then the banks will be indifferent as to where they access reserves from so the demand curve is horizontal (shown in red).
Once the price of reserves falls below the penalty rate, banks will then demand reserves according to their requirments (the legal and the perceived). The higher the market rate of interest, the higher is the opportunity cost of holding reserves and hence the lower will be the demand. As rates fall, the opportunity costs fall and the demand for reserves increases. But in all cases, banks will only seek to hold (in aggregate) the levels consistent with their requirements.
At low interest rates (say zero) banks will hold the legally-required reserves plus a buffer that ensures there is no risk of falling short during the operation of the payments system.
Commercial banks choose to hold reserves to ensure they can meet all their obligations with respect to the clearing house (payments) system. Because there is considerable uncertainty (for example, late-day payment flows after the interbank market has closed), a bank may find itself short of reserves. Depending on the circumstances, it may choose to keep a buffer stock of reserves just to meet these contingencies.
So central bank reserves are intrinsic to the payments system where a mass of interbank claims are resolved by manipulating the reserve balances that the banks hold at the central bank. This process has some expectational regularity on a day-to-day basis but stochastic (uncertain) demands for payments also occur which means that banks will hold surplus reserves to avoid paying any penalty arising from having reserve deficiencies at the end of the day (or accounting period).
To understand what is going on not that the diagram is representing the system-wide demand for bank reserves where the horizontal axis measures the total quantity of reserve balances held by banks while the vertical axis measures the market interest rate for overnight loans of these balances
In this diagram there are no required reserves (to simplify matters). We also initially, abstract from the deposit rate for the time being to understand what role it plays if we introduce it.
Without the deposit rate, the central bank has to ensure that it supplies enough reserves to meet demand while still maintaining its policy rate (the monetary policy setting.
So the model can demonstrate that the market rate of interest will be determined by the central bank supply of reserves. So the level of reserves supplied by the central bank supply brings the market rate of interest into line with the policy target rate.
At the supply level shown as Point A, the central bank can hit its monetary policy target rate of interest given the banks’ demand for aggregate reserves. So the central bank announces its target rate then undertakes monetary operations (liquidity management operations) to set the supply of reserves to this target level.
So contrary to what Mankiw’s textbook tells students the reality is that monetary policy is about changing the supply of reserves in such a way that the market rate is equal to the policy rate.
The central bank uses open market operations to manipulate the reserve level and so must be buying and selling government debt to add or drain reserves from the banking system in line with its policy target.
If there are excess reserves in the system and the central bank didn’t intervene then the market rate would drop towards zero and the central bank would lose control over its target rate (that is, monetary policy would be compromised).
As explained in the blog – Understanding central bank operations – the introduction of a support rate payment (deposit rate) whereby the central bank pays the member banks a return on reserves held overnight changes things considerably.
It clearly can – under certain circumstances – eliminate the need for any open-market operations to manage the volume of bank reserves.
In terms of the diagram, the major impact of the deposit rate is to lift the rate at which the demand curve becomes horizontal (as depicted by the new horizontal red segment moving up via the arrow).
This policy change allows the banks to earn overnight interest on their excess reserve holdings and becomes the minimum market interest rate and defines the lower bound of the corridor within which the market rate can fluctuate without central bank intervention.
So in this diagram, the market interest rate is still set by the supply of reserves (given the demand for reserves) and so the central bank still has to manage reserves appropriately to ensure it can hit its policy target. If there are excess reserves in the system in this case, and the central bank didn’t intervene, then the market rate will drop to the support rate (at Point B).
So if the central bank wants to maintain control over its target rate it can either set a support rate below the desired policy rate (as in Australia) and then use open market operations to ensure the reserve supply is consistent with Point A or set the support (deposit) rate equal to the target policy rate.
The answer to the question is thus False because the simple act of paying interest on reserves does not necessarily eliminate the need for open market operations. It all depends on where the support rate is set. Only if it set equal to the policy rate will there be no need for the central bank to manage liquidity via open market operations.
The following blogs may be of further interest to you:
- Understanding central bank operations
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
Question 4
Continuous budget deficits increase the stock of public spending which might increase the inflation risk if spending exceeds the real capacity of the economy to increase output.
The answer is False.
This question tests whether you understand that budget deficits are just the outcome of two flows which have a finite lifespan. Flows typically feed into stocks (increase or decrease them) and in the case of deficits, under current institutional arrangements, they increase public debt holdings.
So the expenditure impacts of deficit exhaust each period and underpin production and income generation and saving. Aggregate saving is also a flow but can add to stocks of financial assets when stored.
Under current institutional arrangements (where governments unnecessarily issue debt to match its net spending $-for-$) the deficits will also lead to a rise in the stock of public debt outstanding. But of-course, the increase in debt is not a consequence of any “financing” imperative for the government because a sovereign government is never revenue constrained being the monopoly issuer of the currency.
The point is that there is no inflation risk per se with continuous budget deficits. The only time inflation becomes a risk from the demand side if nominal spending outstrips the capacity of the real economy to expand output.
A continuously increasing budget deficit might create those conditions, but a correctly calibrated continuous budget deficit will not because it will be just filling the non-government spending gap.
The following blogs may be of further interest to you:
- Deficit spending 101 – Part 1
- Deficit spending 101 – Part 2
- Deficit spending 101 – Part 3
- Fiscal sustainability 101 – Part 1
- Fiscal sustainability 101 – Part 2
- Fiscal sustainability 101 – Part 3
Premium Question 5:
To reduce trade deficits, Eurozone nations are seeking to restore export competitiveness (within the Eurozone) by domestic deflation (reducing domestic wages and prices relative to other nations) given they do not have a flexible exchange rate. However, export competitiveness may still fall no matter how much some nations deflate.
The answer is True.
The temptation is to accept the rhetoric after understanding the constraints that the EMU places on member countries and conclude that the only way that competitiveness can be restored is to cut wages and prices. That is what the dominant theme emerging from the public debate is telling us.
However, deflating an economy under these circumstance is only part of the story and does not guarantee that a nations competitiveness will be increased.
We have to differentiate several concepts: (a) the nominal exchange rate; (b) domestic price levels; (c) unit labour costs; and (d) the real or effective exchange rate.
It is the last of these concepts that determines the “competitiveness” of a nation. This Bank of Japan explanation of the real effective exchange rate is informative. Their English-language services are becoming better by the year.
Nominal exchange rate (e)
The nominal exchange rate (e) is the number of units of one currency that can be purchased with one unit of another currency. There are two ways in which we can quote a bi-lateral exchange rate. Consider the relationship between the $A and the $US.
- The amount of Australian currency that is necessary to purchase one unit of the US currency ($US1) can be expressed. In this case, the $US is the (one unit) reference currency and the other currency is expressed in terms of how much of it is required to buy one unit of the reference currency. So $A1.60 = $US1 means that it takes $1.60 Australian to buy one $US.
- Alternatively, e can be defined as the amount of US dollars that one unit of Australian currency will buy ($A1). In this case, the $A is the reference currency. So, in the example above, this is written as $US0.625= $A1. Thus if it takes $1.60 Australian to buy one $US, then 62.5 cents US buys one $A. (i) is just the inverse of (ii), and vice-versa.
So to understand exchange rate quotations you must know which is the reference currency. In the remaining I use the first convention so e is the amount of $A which is required to buy one unit of the foreign currency.
International competitiveness
Are Australian goods and services becoming more or less competitive with respect to goods and services produced overseas? To answer the question we need to know about:
- movements in the exchange rate, ee; and
- relative inflation rates (domestic and foreign).
Clearly within the EMU, the nominal exchange rate is fixed between nations so the changes in competitiveness all come down to the second source and here foreign means other nations within the EMU as well as nations beyond the EMU.
There are also non-price dimensions to competitiveness, including quality and reliability of supply, which are assumed to be constant.
We can define the ratio of domestic prices (P) to the rest of the world (Pw) as Pw/P.
For a nation running a flexible exchange rate, and domestic prices of goods, say in the USA and Australia remaining unchanged, a depreciation in Australia’s exchange means that our goods have become relatively cheaper than US goods. So our imports should fall and exports rise. An exchange rate appreciation has the opposite effect.
But this option is not available to an EMU nation so the only way goods in say Greece can become cheaper relative to goods in say, Germany is for the relative price ratio (Pw/P) to change:
- If Pw is rising faster than P, then Greek goods are becoming relatively cheaper within the EMU; and
- If Pw is rising slower than P, then Greek goods are becoming relatively more expensive within the EMU.
The inverse of the relative price ratio, namely (P/Pw) measures the ratio of export prices to import prices and is known as the terms of trade.
The real exchange rate
Movements in the nominal exchange rate and the relative price level (Pw/P) need to be combined to tell us about movements in relative competitiveness. The real exchange rate captures the overall impact of these variables and is used to measure our competitiveness in international trade.
The real exchange rate (R) is defined as:
R = (e.Pw/P)
where P is the domestic price level specified in $A, and Pw is the foreign price level specified in foreign currency units, say $US.
The real exchange rate is the ratio of prices of goods abroad measured in $A (ePw) to the $A prices of goods at home (P). So the real exchange rate, R adjusts the nominal exchange rate, e for the relative price levels.
For example, assume P = $A10 and Pw = $US8, and e = 1.60. In this case R = (8×1.6)/10 = 1.28. The $US8 translates into $A12.80 and the US produced goods are more expensive than those in Australia by a ratio of 1.28, ie 28%.
A rise in the real exchange rate can occur if:
- the nominal e depreciates; and/or
- Pw rises more than P, other things equal.
A rise in the real exchange rate should increase our exports and reduce our imports.
A fall in the real exchange rate can occur if:
- the nominal e appreciates; and/or
- Pw rises less than P, other things equal.
A fall in the real exchange rate should reduce our exports and increase our imports.
In the case of the EMU nation we have to consider what factors will drive Pw/P up and increase the competitive of a particular nation.
If prices are set on unit labour costs, then the way to decrease the price level relative to the rest of the world is to reduce unit labour costs faster than everywhere else.
Unit labour costs are defined as cost per unit of output and are thus ratios of wage (and other costs) to output. If labour costs are dominant (we can ignore other costs for the moment) so total labour costs are the wage rate times total employment = w.L. Real output is Y.
So unit labour costs (ULC) = w.L/Y.
L/Y is the inverse of labour productivity(LP) so ULCs can be expressed as the w/(Y/L) = w/LP.
So if the rate of growth in wages is faster than labour productivity growth then ULCs rise and vice-versa. So one way of cutting ULCs is to cut wage levels which is what the austerity programs in the EMU nations (Ireland, Greece, Portugal etc) are attempting to do.
But LP is not constant. If morale falls, sabotage rises, absenteeism rises and overall investment falls in reaction to the extended period of recession and wage cuts then productivity is likely to fall as well. Thus there is no guarantee that ULCs will fall by any significant amount.
Bill, Re Q1:
The question was not will the government sector be in deficit or surplus but what would the magnitude of the deficit/surplus be.
That it’s going to be in deficit is obvious, by inspection. The question however was by how much, in %GDP terms.
And you can’t calcuate that unless you have the relative magnitude of the other balances.
Sticking my neck out here but I think the answer should be True.
Bill,
Someone in Congress been reading MMT?
http://www.foxnews.com/politics/2011/10/14/rep-jesse-jackson-calls-on-government-to-hire-all-unemployed-americans-for/
For Q1 and assuming you are using:
current account deficit = gov’t deficit + private deficit
then I agree with John Armour
I also believe this is possible:
current account deficit = gov’t deficit + private deficit + currency printing entity deficit with currency and no bond/loan attached
I’ll need to check my phrasing, but I’d like to go over Q2 if it said:
2. The private sector is wealthier [in the present but may not be in the future] if the government matches its deficit spending with bond issues …
I’m assuming the gov’t budget is set up to make both interest and principal payments so the debt can be paid off at maturity so there is no rollover risk.
Q2, “… if the government just spent without issuing bonds (that is, instructed the central bank to credit bank accounts).
IMO, this whole credit accounts idea makes what is going on actually more difficult than it really is.
Let’s say the gov’t printed up some currency with no bond/loan attached and mailed it to me. I then take it to a bank and deposit it. Doesn’t the accounting end up being the same?
Q3, “Ignoring any reserve requirements”. So I assume raising the reserve requirement would work too.
“Modern Monetary Theory (MMT) explains how central banks sell bonds to drain excess bank reserves in order to maintain their given interest rate setting.”
And is the interest rate (central bank overnight rate) setting mostly about attempting to control debt levels? For example, an economy needs $1 million more in spending and has a 10% reserve requirement. The gov’t spends $1 million with no bond attached. The overnight rate goes to zero(0). Next, entities start borrowing to spend until the borrowing total reaches $10 million. Shouldn’t that get the central bank overnight rate back to where it was? However, instead of $1 million in spending, there is $11 million in spending causing price inflation.
Also, “In Mankiw’s Principles of Economics (Chapter 27 First Edition) he say that the central bank has “two related jobs”. The first is to “regulate the banks and ensure the health of the financial system” and the second “and more important job”:
… is to control the quantity of money that is made available to the economy, called the money supply. Decisions by policymakers concerning the money supply constitute monetary policy (emphasis in original).”
I’d like to see mankiw and others who say the “money supply” is basically the medium of exchange supply vs. scott sumner and others who say the “money supply” is monetary base “fight” over their definitions.
It seems to me Q4 is true if “stock” is changed to “flow”.
“A continuously increasing budget deficit might create those conditions, but a correctly calibrated continuous budget deficit will not because it will be just filling the non-government spending gap.”
If the budget deficit is with debt, then I believe there will eventually be other problems in an economy like:
savings of the rich = dissavings of the gov’t (preferably with debt) + dissavings of the lower and middle class (preferably with debt)
If the budget deficit is without debt, then I believe there is/are better way(s) to get more medium of exchange into an economy.
Re: John Armour says:
Sunday, October 16, 2011 at 7:28
I agree with John, you cannot tell what the % balance(a balance can be surplus or deficit) will be until you know the other 2.
“A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances). “
Another vote for the answer to Q.1 being true: the question is clearly about magnitude, not sign.
I also think that the answer to Q.3 should be true, since it indicates that a level of interest is paid that results in the same outcome (as bond sales), not merely that some unspecified level is paid:
…central banks sell bonds to drain excess bank reserves in order to maintain their given interest rate setting. We know that the same outcome can be achieved by paying interest…
Signed – a sore loser
It is often stated in MMT that if the Fed were to pay its target rate on reserves there would be no need to sell treasuries. In that case excess reserves would apparently build up dollar for dollar with deficit spending. The need for interbank loans would vanish, so banks would be subsidized for having reserves and the Fed rate would have no monetary leverage on the bank lending rates. Would not fiscal means be needed to manage the economy just as in the case of zero interest on reserves? A discussion of the consequences for bank operations of this kind of decision has not yet met my eyes. Is there a reference to such a discussion? Thanks.
Dan
I don’t think the Fed rate exerts leverage on commercial bank lending policy except indirectly by establishing a benchmark against which risk is weighed, so regardless of whether the Fed pays interest on reserves, or seeks to hit the target rate through open market operations, I think the effect is the same.
If a bank was short of reserves however and had to top up via the Fed’s discount window, I imagine the penalty that attaches to using that facility would have a more direct effect on lending policy as it directly affects the bank’s costs.
John,
Thanks for your reply. As reserves inevitably accumulate no bank will have to top up its reserves. Every bank will have excess reserves. If that occurs the rate might as well be zero, as the effect of monetary policy will be nil. There might be a lot of competition among banks regarding what they pay their depositors that is now set by the overnight rate. I imagine banks will completely revise their business plans.
What am I missing?
Dan,
This is what I think happens.
When the government deficit spends it credits the reserve account of the recipient’s bank. The recipient then spends that money into the broader economy, which results in a series of adjustments (up and down) to the reserve accounts of other banks, as they accept and clear the resulting flow of cheques, as the deficit money works its way through the economy.
But deficit spending stimulates economic activity, and this increased activity creates tax liabilities. And I think it’s the payment of these tax liabilities that ensures that reserves don’t just keep building up, unlike QE.
Furthermore, the stimulus effect of the deficit spending could also have an effect on the horizontal circuit where endogenous money is created (by lending), thus creating a need for the commercial banks to maintain reserves for either operational reasons, or statutory reserve requirements if there are any.
Finally, given that depositor’s money is used to maintain reserves (not lent, as is the common belief) I guess banks could also lower the deposit rate and slow down the inflow of deposits ?
Dan,
Here’s a paper I found that covers some of the issues we’ve been talking about:
“Endogenous Money: Structuralist and Horizontalist” by Wray. Levy Institute Working Paper No. 512.
Sorry, no link. Try google.
Thanks, John,
I’ll look up the paper. I might work on some numbers. It just seems that if the excess reserves accumulate exactly as deficits add up, every bank would never have to top off its tank. If that were assumed, perhaps as a limiting case, who would care about the Fed funds rate? Maybe if the TT&Ls were also abolished swings in reserves would be large enough to require bank reserve adjustments.
Am off googling.
Dan
To: John Armour,
Just in case you are still hanging around this page…
I found the Wray reference, thank you very much.
Later, I found what I was looking for in this Scott Fullwiler paper that might interest you.
http://www.cfeps.org/pubs/wp-pdf/WP38-Fullwiler.pdf
Dan
Hi Dan,
I popped back in to see if Bill or any of the MMT guns had come to our rescue with Question 1, but alas, the thread so soon grows cold, as Oscar Wilde might’ve put it.
Thanks for that excellent link. Yet more pieces placed in the giant banking jigsaw puzzle.