Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday quiz – February 25, 2012 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you understand the reasoning behind the answers. If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
If a nation’s external sector is in balance (and thus making no contribution to real GDP growth) then the private domestic sector cannot save overall if the government runs a balanced budget.
The answer is True.
This is a question about sectoral balances. Skip the derivation if you are familiar with the framework.
First, you need to understand the basic relationship between the sectoral flows and the balances that are derived from them. The flows are derived from the National Accounting relationship between aggregate spending and income. So:
(1) Y = C + I + G + (X – M)
where Y is GDP (income), C is consumption spending, I is investment spending, G is government spending, X is exports and M is imports (so X – M = net exports).
Another perspective on the national income accounting is to note that households can use total income (Y) for the following uses:
(2) Y = C + S + T
where S is total saving and T is total taxation (the other variables are as previously defined).
You than then bring the two perspectives together (because they are both just “views” of Y) to write:
(3) C + S + T = Y = C + I + G + (X – M)
You can then drop the C (common on both sides) and you get:
(4) S + T = I + G + (X – M)
Then you can convert this into the familiar sectoral balances accounting relations which allow us to understand the influence of fiscal policy over private sector indebtedness.
So we can re-arrange Equation (4) to get the accounting identity for the three sectoral balances – private domestic, government budget and external:
(S – I) = (G – T) + (X – M)
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.
Another way of saying this is that total private savings (S) is equal to private investment (I) plus the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
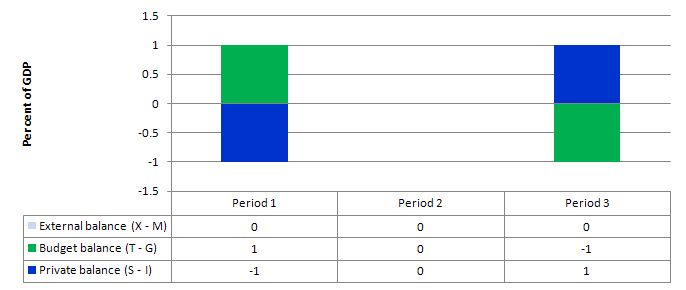
Consider the following graph which shows three situations where the external sector is in balance.
Period 1, the budget is in surplus (T – G = 1) and the private balance is in deficit (S – I = -1). With the external balance equal to 0, the general rule that the government surplus (deficit) equals the non-government deficit (surplus) applies to the government and the private domestic sector.
In Period 3, the budget is in deficit (T – G = -1) and this provides some demand stimulus in the absence of any impact from the external sector, which allows the private domestic sector to save (S – I = 1).
Period 2, is the case in point and the sectoral balances show that if the external sector is in balance and the government is able to achieve a fiscal balance, then the private domestic sector must also be in balance.
The movements in income associated with the spending and revenue patterns will ensure these balances arise. The problem is that if the private domestic sector desires to save overall then this outcome will be unstable and would lead to changes in the other balances as national income changed in response to the decline in private spending.
So under the conditions specified in the question, the private domestic sector cannot save. The government would be undermining any desire to save by not providing the fiscal stimulus necessary to increase national output and income so that private households/firms could save.
You may wish to read the following blogs for more information:
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
- Barnaby, better to walk before we run
- Saturday Quiz – June 19, 2010 – answers and discussion
Question 2:
A tax increase, which aims to increase tax revenue at the current level of national income by $x, will have a smaller initial negative impact on aggregate demand than a government spending cut of $x?
The answer is True.
The question is only seeking an understanding of the initial drain on the spending stream rather than the fully exhausted multiplied contraction of national income that will result. It is clear that the tax increase increase will have two effects: (a) some initial demand drain; and (b) it reduces the value of the multiplier, other things equal.
We are only interested in the first effect rather than the total effect. But I will give you some insight also into what the two components of the tax result might imply overall when compared to the impact on demand motivated by an decrease in government spending.
To give you a concrete example which will consolidate the understanding of what happens, imagine that the marginal propensity to consume out of disposable income is 0.8 and there is only one tax rate set at 0.20. So for every extra dollar that the economy produces the government taxes 20 cents leaving 80 cents in disposable income. In turn, households then consume 0.8 of this 80 cents which means an injection of 64 cents goes into aggregate demand which them multiplies as the initial spending creates income which, in turn, generates more spending and so on.
Government spending cut
A cut in government spending (say of $1000) is what we call an exogenous withdrawal from the aggregate spending stream and this directly reduces aggregate demand by that amount. So it might be the cancellation of a long-standing order for $1000 worth of gadget X. The firm that produces gadget X thus reduces production of the good or service by the fall in orders ($1000) (if they deem the drop in sales to be permanent) and as a result incomes of the productive factors working for and/or used by the firm fall by $1000. So the initial fall in aggregate demand is $1000.
This initial fall in national output and income would then induce a further fall in consumption by 64 cents in the dollar so in Period 2, aggregate demand would decline by $640. Output and income fall further by the same amount to meet this drop in spending. In Period 3, aggregate demand falls by 0.8 x 0.8 x $640 and so on. The induced spending decrease gets smaller and smaller because some of each round of income drop is taxed away, some goes to a decline in imports and some manifests as a decline in saving.
Tax-increase induced contraction
The contraction coming from a tax-cut does not directly impact on the spending stream in the same way as the cut in government spending.
First, imagine the government worked out a tax rise cut that would reduce its initial budget deficit by the same amount as would have been the case if it had cut government spending (so in our example, $1000).
In other words, disposable income at each level of GDP falls initially by $1000. What happens next?
Some of the decline in disposable income manifests as lost saving (20 cents in each dollar that disposable income falls in the example being used). So the lost consumption is equal to the marginal propensity to consume out of disposable income times the drop in disposable income (which if the MPC is less than 1 will be lower than the $1000).
In this case the reduction in aggregate demand is $800 rather than $1000 in the case of the cut in government spending.
What happens next depends on the parameters of the macroeconomic system. The multiplied fall in national income may be higher or lower depending on these parameters. But it will never be the case that an initial budget equivalent tax rise will be more damaging to national income than a cut in government spending.
Note in answering this question I am disregarding all the nonsensical notions of Ricardian equivalence that abound among the mainstream doomsayers who have never predicted anything of empirical note! I am also ignoring the empirically-questionable mainstream claims that tax increases erode work incentives which force workers to supply less labour.
You may wish to read the following blogs for more information:
Question 3:
During a recession, a government should use expansionary fiscal policy to restore trend real GDP growth if it wants to reduce unemployment rate.
The answer is False.
To see why, we might usefully construct a scenario that will explicate the options available to a government:
- Trend real GDP growth rate is 3 per cent annum.
- Labour productivity growth (that is, growth in real output per person employed) is growing at 2 per cent per annum. So as this grows less employment in required per unit of output.
- The labour force is growing by 1.5 per cent per annum. Growth in the labour force adds to the employment that has to be generated for unemployment to stay constant (or fall).
- The average working week is constant in hours. So firms are not making hours adjustments up or down with their existing workforce. Hours adjustments alter the relationship between real GDP growth and persons employed.
We can use this scenario to explore the different outcomes.
The trend rate of real GDP growth doesn’t relate to the labour market in any direct way. The late Arthur Okun is famous (among other things) for estimating the relationship that links the percentage deviation in real GDP growth from potential to the percentage change in the unemployment rate – the so-called Okun’s Law.
The algebra underlying this law can be manipulated to estimate the evolution of the unemployment rate based on real output forecasts.
From Okun, we can relate the major output and labour-force aggregates to form expectations about changes in the aggregate unemployment rate based on output growth rates. A series of accounting identities underpins Okun’s Law and helps us, in part, to understand why unemployment rates have risen.
Take the following output accounting statement:
(1) Y = LP*(1-UR)LH
where Y is real GDP, LP is labour productivity in persons (that is, real output per unit of labour), H is the average number of hours worked per period, UR is the aggregate unemployment rate, and L is the labour-force. So (1-UR) is the employment rate, by definition.
Equation (1) just tells us the obvious – that total output produced in a period is equal to total labour input [(1-UR)LH] times the amount of output each unit of labour input produces (LP).
Using some simple calculus you can convert Equation (1) into an approximate dynamic equation expressing percentage growth rates, which in turn, provides a simple benchmark to estimate, for given labour-force and labour productivity growth rates, the increase in output required to achieve a desired unemployment rate.
Accordingly, with small letters indicating percentage growth rates and assuming that the average number of hours worked per period is more or less constant, we get:
(2) y = lp + (1 – ur) + lf
Re-arranging Equation (2) to express it in a way that allows us to achieve our aim (re-arranging just means taking and adding things to both sides of the equation):
(3) ur = 1 + lp + lf – y
Equation (3) provides the approximate rule of thumb – if the unemployment rate is to remain constant, the rate of real output growth must equal the rate of growth in the labour-force plus the growth rate in labour productivity.
It is an approximate relationship because cyclical movements in labour productivity (changes in hoarding) and the labour-force participation rates can modify the relationships in the short-run. But it provides reasonable estimates of what happens when real output changes.
The sum of labour force and productivity growth rates is referred to as the required real GDP growth rate – required to keep the unemployment rate constant.
Remember that labour productivity growth (real GDP per person employed) reduces the need for labour for a given real GDP growth rate while labour force growth adds workers that have to be accommodated for by the real GDP growth (for a given productivity growth rate).
So in the example, the required real GDP growth rate is 3.5 per cent per annum and if policy only aspires to keep real GDP growth at its trend growth rate of 3 per cent annum, then the output gap that emerges is 0.5 per cent per annum.
The unemployment rate will rise by this much (give or take) and reflects the fact that real output growth is not strong enough to both absorb the new entrants into the labour market and offset the employment losses arising from labour productivity growth.
So the appropriate fiscal strategy does not relate to “trend output” but to the required real GDP growth rate given labour force and productivity growth. The two growth rates might be consistent but then they need not be. That lack of concordance makes the proposition false.
The following blog may be of further interest to you:
Question 4:
In many nations, private households are increasing their saving ratios (from disposable income) and firms are declining to invest. These trends indicate that budget deficits have to be higher to avoid further employment losses.
The answer is False.
The answer also relates to the sectoral balances framework outlined in detail above. When the private domestic sector decides to lift its saving ratio, we normally think of this in terms of households reducing consumption spending. However, it could also be evidenced by a drop in investment spending (building productive capacity).
The normal inventory-cycle view of what happens next goes like this. Output and employment are functions of aggregate spending. Firms form expectations of future aggregate demand and produce accordingly. They are uncertain about the actual demand that will be realised as the output emerges from the production process.
The first signal firms get that household consumption is falling is in the unintended build-up of inventories. That signals to firms that they were overly optimistic about the level of demand in that particular period.
Once this realisation becomes consolidated, that is, firms generally realise they have over-produced, output starts to fall. Firms layoff workers and the loss of income starts to multiply as those workers reduce their spending elsewhere.
At that point, the economy is heading for a recession. Interestingly, the attempts by households overall to increase their saving ratio may be thwarted because income losses cause loss of saving in aggregate – the is the Paradox of Thrift. While one household can easily increase its saving ratio through discipline, if all households try to do that then they will fail. This is an important statement about why macroeconomics is a separate field of study.
Typically, the only way to avoid these spiralling employment losses would be for an exogenous intervention to occur – in the form of an expanding public deficit. The budget position of the government would be heading towards, into or into a larger deficit depending on the starting position as a result of the automatic stabilisers anyway.
So an intuitive reasoning suggests that a demand gap opens and the only way to stop the economy from contracting with employment losses if it the government fills the spending gap by expanding net spending (its deficit).
However, this would ignore the movements in the third sector – there is also an external sector. It is possible that at the same time that the households are reducing their consumption as an attempt to lift the saving ratio, net exports boom. A net exports boom adds to aggregate demand (the spending injection via exports is greater than the spending leakage via imports).
So it is possible that the public budget balance could actually go towards surplus and the private domestic sector increase its saving ratio if net exports were strong enough.
The important point is that the three sectors add to demand in their own ways. Total GDP and employment are dependent on aggregate demand. Variations in aggregate demand thus cause variations in output (GDP), incomes and employment. But a variation in spending in one sector can be made up via offsetting changes in the other sectors.
The following blogs may be of further interest to you:
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
- Saturday Quiz – May 22, 2010 – answers and discussion
Premium Question 5:
If the external sector is accumulating financial claims on the local economy and the GDP growth rate is lower than the real interest rate, then the private domestic sector and the government sector can run surpluses without damaging employment growth.
The answer is False.
When the external sector is accumulating financial claims on the local economy it must mean the current account is in deficit – so the external balance is in deficit. Under these conditions it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the national accounting rules and income adjustments will always ensure that is the case.
The relationship between the rate of GDP growth and the real interest rate doesn’t alter this result and was included as superflous information to test the clarity of your understanding.
To understand this we need to begin with the national accounts which underpin the basic income-expenditure model that is at the heart of introductory macroeconomics. See the answer to Question 1 for the background conceptual development.
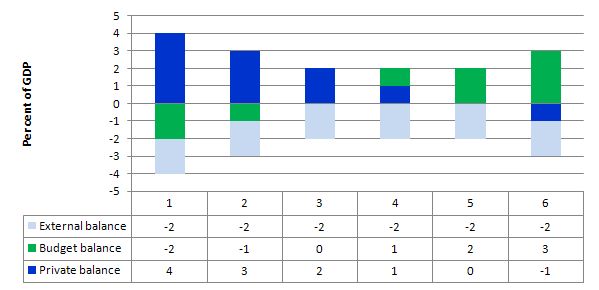
Consider the following graph and associated table of data which shows six states. All states have a constant external deficit equal to 2 per cent of GDP (light-blue columns).
State 1 show a government running a surplus equal to 2 per cent of GDP (green columns). As a consequence, the private domestic balance is in deficit of 4 per cent of GDP (royal-blue columns). This cannot be a sustainable growth strategy because eventually the private sector will collapse under the weight of its indebtedness and start to save. At that point the fiscal drag from the budget surpluses will reinforce the spending decline and the economy would go into recession.
State 2 shows that when the budget surplus moderates to 1 per cent of GDP the private domestic deficit is reduced.
State 3 is a budget balance and then the private domestic deficit is exactly equal to the external deficit. So the private sector spending more than they earn exactly funds the desire of the external sector to accumulate financial assets in the currency of issue in this country.
States 4 to 6 shows what happens when the budget goes into deficit – the private domestic sector (given the external deficit) can then start reducing its deficit and by State 5 it is in balance. Then by State 6 the private domestic sector is able to net save overall (that is, spend less than its income).
Note also that the government balance equals exactly $-for-$ (as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances). This is also a basic rule derived from the national accounts.
Most countries currently run external deficits. The crisis was marked by households reducing consumption spending growth to try to manage their debt exposure and private investment retreating. The consequence was a major spending gap which pushed budgets into deficits via the automatic stabilisers.
The only way to get income growth going in this context and to allow the private sector surpluses to build was to increase the deficits beyond the impact of the automatic stabilisers. The reality is that this policy change hasn’t delivered large enough budget deficits (even with external deficits narrowing). The result has been large negative income adjustments which brought the sectoral balances into equality at significantly lower levels of economic activity.
The following blogs may be of further interest to you:
Hi Bill,
I understand this:
“Another way of saying this is that total private savings (S) is equal to private investment (I) plus the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.”
Which is just a verbal formulation of this:
S = I + (G-T) + (X-M)
That is straightforward.
Here’s my question.
If (X-M)= 0
and
(G-T) = 0
Then our formulation reduces to: S = I
So isn’t it the case that if net exports is zero, the government budget can be balanced and S > 0 so long as I > 0 – therefore what we should say is that when the current account is balanced and the government budget is balanced, then private sector savings is limited to the savings made possible by investment?
best,
George
George,
If the other sectors are in balance then private sector savings is limited to the savings that existed at the moment those sectors were in balance. Total savings cannot change from then on until one of the other sectors moves out of balance.
George,
If G-T=0 and X-M=0, then as a matter of accounting S-I=0 as well.
George,
I see what you are saying now. I agree, S would equal I, which is the same as saying S – I = 0.
Kind Regards
About S=I, what if some entity wants to save but not invest? What’s happening?
What happens when saving happens in the medium of exchange or something medium of exchange like?
imo, Q1 is true only under certain assumptions.
current account deficit = gov’t deficit plus private deficit
I believe that assumes the currency printing entity is inactive and all new medium of exchange has to be borrowed into existence.
I think this is possible. Assume CA deficit = 0, gov’t deficit = 0, and break down the private sector into rich and lower/middle class.
current account deficit = gov’t deficit plus rich deficit plus lower/middle class deficit plus currency printing entity deficit
0 = 0 + (+2) + (+2) +(-4)
In relation to my 15:32 comment,
rich surplus = gov’t deficit (preferably with debt) plus lower and middle class deficit (preferably with debt)
if the currency printing entity is not involved directly.
Q3, “So the appropriate fiscal strategy does not relate to “trend output” but to the required real GDP growth rate given labour force and productivity growth. The two growth rates might be consistent but then they need not be. That lack of concordance makes the proposition false.”
I believe some of that needs to spelled out in the question.
I have another question though. I believe you are assuming something close to productivity growth plus labor growth equals real Aggregate Supply (AS) and that whatever real AS is that is what real GDP should be. I believe that can be true but does not have to be.
Q5 and back to my 15:32 comment, I don’t see why this is not possible.
current account deficit = gov’t deficit plus rich deficit plus lower/middle class deficit plus currency printing entity deficit
(-2) = (+2) + (+1) + (+1) +(-6)
I’m of the opinion that Houston we have a medium of exchange problem (too much debt both private and gov’t)
“About S=I, what if some entity wants to save but not invest? What’s happening?”
Banks buffer through time.
Dear Bill,
Apologies if I have overstepped a boundary in your comments section.
Sincerely,
jrbarch
Dear jrbarch (at 2012/02/28 at 19:42)
I cannot imagine you overstepping any “boundary”. I am unsure what you are referring to.
best wishes
bill
Bill,
I’m curious as to whether I’ve represented your views correctly. See below…
—
Paulie,
A few points:
I could be wrong about this, but I think that…
1) From period 1 to period 2, both Investment spending can increase and Savings can increase, and therefore (S-I) can remain at zero and, therefore, be in balance with (G-T) and (X-M).
That’s just a point of logic – of basic algebra.
2) The empirical reality behind this is that there can be private sector credit expansion to fund Investment, which would make possible additional Savings without a change in (G-T).
Warren Mosler writes about Investment making Savings possible in “The Seven Deadly Innocent Frauds.”
The problem, of course, is that this Savings would be offset by an increase of debt, so it would result in no new net financial assets.
3) The reason this is confusing is that the macro-variables G, T, X, and M are all flows *to and from * the government and foreign sectors respectively, but S and I are macro-variables that describe flows *within* the private sector (which includes the banking system, which is kind of a piece of the government sector – so it’s not all as logically clean as it could be)
Of course as a matter of fact the private sector wants to accumulate net claims on the government and foreign sectors, which is why S is (almost always) greater than I.
Bill, is that all true?
best,
George