Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday quiz – June 23, 2012 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you understand the reasoning behind the answers. If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
An external surplus is a necessary but not sufficient condition for a nation that wishes to grow during a period of fiscal surpluses and private domestic deleveraging.
The answer is True.
This is a question about the relative magnitude of the sectoral balances – the government budget balance, the external balance and the private domestic balance. The balances taken together always add to zero because they are derived as an accounting identity from the national accounts. The balances reflect the underlying economic behaviour in each sector which is interdependent – given this is a macroeconomic system we are considering.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X – M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I – S) + (G – T) + (X – M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
- The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
- The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
- The Current Account balance (X – M) – positive if in surplus, negative if in deficit.
These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
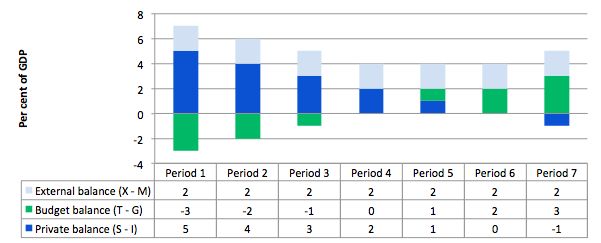
The following graph with accompanying data table lets you see the evolution of the balances expressed in terms of percent of GDP. In each period I just held the budget balance at a constant surplus (2 per cent of GDP) (green bars). This is is artificial because as economic activity changes the automatic stabilisers would lead to endogenous changes in the budget balance. But we will just assume there is no change for simplicity. It doesn’t violate the logic.
To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.
If the nation is running an external surplus it means that the contribution to aggregate demand from the external sector is positive – that is net addition to spending which would increase output and national income.
The external surplus also means that foreigners are decreasing financial claims denominated in the local currency. Given that exports represent a real cost and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.
A fiscal surplus means the government is spending less than it is taking out of the economy via taxations which puts a drag on aggregate demand and constrains the ability of the economy to grow. So the question is what are the relative magnitudes of the external add and the budget subtract from income?
The following graph shows the range of options for a given external surplus (of 2 per cent of GDP).
In Periods 1 to 5, the private sector is saving because the public sector does not negate the overall contribution of the external sector to demand and hence growth. Clearly, the larger is the budget deficit the greater is the capacity of the private sector to save overall because the growth in income would be stronger.
In Periods 4 and 5, the budget moves from deficit to balance then surplus, yet the private sector can still net save. That is because the fiscal drag coming from the budget in Period 4 is zero and in Period 5 less than the aggregate demand add derived from the external sector.
In Periods 6 and 7, the private sector stops net saving because the fiscal drag coming from the budget surplus offsets (Period 6) and then overwhelms (Period 7) the aggregate demand add from the external sector.
The general rule when the economy runs an external surplus is that the private domestic sector will be able to net save if the budget surplus is less than the external surplus.
That is why the external surplus is necessary but not sufficient. It relies on the budget surplus being large enough for the private domestic sector to be able to net save.
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
- Saturday Quiz – June 19, 2010 – answers and discussion
Question 2:
If central banks stopped paying a return to the private banks on the reserves they hold with the central bank then the private banks would have a greater incentive to advance credit to the private sector.
The answer is False.
The facts are as follows. First, central banks will always provided enough reserve balances to the commercial banks at a price it sets using a combination of overdraft/discounting facilities and open market operations.
Second, if the central bank didn’t provide the reserves necessary to match the growth in deposits in the commercial banking system then the payments system would grind to a halt and there would be significant hikes in the interbank rate of interest and a wedge between it and the policy (target) rate – meaning the central bank’s policy stance becomes compromised.
Third, any reserve requirements within this context while legally enforceable (via fines etc) do not constrain the commercial bank credit creation capacity. Central bank reserves (the accounts the commercial banks keep with the central bank) are not used to make loans. They only function to facilitate the payments system (apart from satisfying any reserve requirements).
Fourth, banks make loans to credit-worthy borrowers and these loans create deposits. If the commercial bank in question is unable to get the reserves necessary to meet the requirements from other sources (other banks) then the central bank has to provide them. But the process of gaining the necessary reserves is a separate and subsequent bank operation to the deposit creation (via the loan).
Fifth, if there were too many reserves in the system (relative to the banks’ desired levels to facilitate the payments system and the required reserves then competition in the interbank (overnight) market would drive the interest rate down. This competition would be driven by banks holding surplus reserves (to their requirements) trying to lend them overnight. The opposite would happen if there were too few reserves supplied by the central bank. Then the chase for overnight funds would drive rates up.
In both cases the central bank would lose control of its current policy rate as the divergence between it and the interbank rate widened. This divergence can snake between the rate that the central bank pays on excess reserves (this rate varies between countries and overtime but before the crisis was zero in Japan and the US) and the penalty rate that the central bank seeks for providing the commercial banks access to the overdraft/discount facility.
So the aim of the central bank is to issue just as many reserves that are required for the law and the banks’ own desires.
But banks do not lend reserves. They are used to facilitate the so-called payments system so that all transactions that are drawn on the various banks (cheques etc) clear at the end of each day. Clearly banks prefer to earn a return on reserves that it deems are in excess of its clearing house (payments system) requirements.
But in the absence of such a return being paid by the central bank the only consequence would be that the banks (overall) would have zero interest balances.
You might like to read this blog for further information:
Question 3:
Spain has reduced its budget deficit over the last 12 months through austerity. A declining deficit indicates that the government fiscal stance is becoming more contractionary.
The answer is False.
Intuitively, we might think that if the deficit rises the government must be pursuing an expansionary fiscal policy. But intuition is not always a good guide and doesn’t replace understanding.
The question is exploring the issue of decomposing the observed budget balance into the discretionary (now called structural) and cyclical components. The latter component is driven by the automatic stabilisers that are in-built into the budget process.
The budget balance is the difference between total government revenue and total government outlays. So if total revenue is greater than outlays, the budget is in surplus and vice versa. It is a simple matter of accounting with no theory involved. However, the budget balance is used by all and sundry to indicate the fiscal stance of the government.
So if the budget is in surplus it is often concluded that the fiscal impact of government is contractionary (withdrawing net spending) and if the budget is in deficit we say the fiscal impact expansionary (adding net spending).
Further, a rising deficit (falling surplus) is often considered to be reflecting an expansionary policy stance and vice versa. What we know is that a rising deficit may, in fact, indicate a contractionary fiscal stance – which, in turn, creates such income losses that the automatic stabilisers start driving the budget back towards (or into) deficit.
So the complication is that we cannot conclude that changes in the fiscal impact reflect discretionary policy changes. The reason for this uncertainty clearly relates to the operation of the automatic stabilisers.
To see this, the most simple model of the budget balance we might think of can be written as:
Budget Balance = Revenue – Spending.
Budget Balance = (Tax Revenue + Other Revenue) – (Welfare Payments + Other Spending)
We know that Tax Revenue and Welfare Payments move inversely with respect to each other, with the latter rising when GDP growth falls and the former rises with GDP growth. These components of the budget balance are the so-called automatic stabilisers
In other words, without any discretionary policy changes, the budget balance will vary over the course of the business cycle. When the economy is weak – tax revenue falls and welfare payments rise and so the budget balance moves towards deficit (or an increasing deficit). When the economy is stronger – tax revenue rises and welfare payments fall and the budget balance becomes increasingly positive. Automatic stabilisers attenuate the amplitude in the business cycle by expanding the budget in a recession and contracting it in a boom.
So just because the budget goes into deficit doesn’t allow us to conclude that the Government has suddenly become of an expansionary mind. In other words, the presence of automatic stabilisers make it hard to discern whether the fiscal policy stance (chosen by the government) is contractionary or expansionary at any particular point in time.
To overcome this uncertainty, economists devised what used to be called the Full Employment or High Employment Budget. In more recent times, this concept is now called the Structural Balance. The change in nomenclature is very telling because it occurred over the period that neo-liberal governments began to abandon their commitments to maintaining full employment and instead decided to use unemployment as a policy tool to discipline inflation.
The Full Employment Budget Balance was a hypothetical construct of the budget balance that would be realised if the economy was operating at potential or full employment. In other words, calibrating the budget position (and the underlying budget parameters) against some fixed point (full capacity) eliminated the cyclical component – the swings in activity around full employment.
So a full employment budget would be balanced if total outlays and total revenue were equal when the economy was operating at total capacity. If the budget was in surplus at full capacity, then we would conclude that the discretionary structure of the budget was contractionary and vice versa if the budget was in deficit at full capacity.
The calculation of the structural deficit spawned a bit of an industry in the past with lots of complex issues relating to adjustments for inflation, terms of trade effects, changes in interest rates and more.
Much of the debate centred on how to compute the unobserved full employment point in the economy. There were a plethora of methods used in the period of true full employment in the 1960s. All of them had issues but like all empirical work – it was a dirty science – relying on assumptions and simplifications. But that is the nature of the applied economist’s life.
As I explain in the blogs cited below, the measurement issues have a long history and current techniques and frameworks based on the concept of the Non-Accelerating Inflation Rate of Unemployment (the NAIRU) bias the resulting analysis such that actual discretionary positions which are contractionary are seen as being less so and expansionary positions are seen as being more expansionary.
The result is that modern depictions of the structural deficit systematically understate the degree of discretionary contraction coming from fiscal policy.
You might like to read these blogs for further information:
Question 4:
A central bank running a policy rate of near zero could always directly purchase Treasury debt to facilitate the government’s budget deficit without compromising its monetary policy stanc
The answer is False.
The Federal Reserve could easily directly purchase Treasury debt to facilitate the US Government’s budget deficit but not because its short-term policy rate is already so low.
They could also do the same with higher positive policy rates by ensuring they offer a support rate on the excess reserves.
So what is the explanation?
The central bank conducts what are called liquidity management operations for two reasons. First, it has to ensure that all private cheques (that are funded) clear and other interbank transactions occur smoothly as part of its role of maintaining financial stability. Second, it must maintain aggregate bank reserves at a level that is consistent with its target policy setting given the relationship between the two.
So operating factors link the level of reserves to the monetary policy setting under certain circumstances. These circumstances require that the return on “excess” reserves held by the banks is below the monetary policy target rate. In addition to setting a lending rate (discount rate), the central bank also sets a support rate which is paid on commercial bank reserves held by the central bank.
Commercial banks maintain accounts with the central bank which permit reserves to be managed and also the clearing system to operate smoothly. In addition to setting a lending rate (discount rate), the central bank also can set a support rate which is paid on commercial bank reserves held by the central bank (which might be zero).
Many countries (such as Australia, Canada and zones such as the European Monetary Union) maintain a default return on surplus reserve accounts (for example, the Reserve Bank of Australia pays a default return equal to 25 basis points less than the overnight rate on surplus Exchange Settlement accounts). Other countries like Japan and the US have typically not offered a return on reserves until the onset of the current crisis.
If the support rate is zero then persistent excess liquidity in the cash system (excess reserves) will instigate dynamic forces which would drive the short-term interest rate to zero unless the government sells bonds (or raises taxes). This support rate becomes the interest-rate floor for the economy.
The short-run or operational target interest rate, which represents the current monetary policy stance, is set by the central bank between the discount and support rate. This effectively creates a corridor or a spread within which the short-term interest rates can fluctuate with liquidity variability. It is this spread that the central bank manages in its daily operations.
In most nations, commercial banks by law have to maintain positive reserve balances at the central bank, accumulated over some specified period. At the end of each day commercial banks have to appraise the status of their reserve accounts. Those that are in deficit can borrow the required funds from the central bank at the discount rate.
Alternatively banks with excess reserves are faced with earning the support rate which is below the current market rate of interest on overnight funds if they do nothing. Clearly it is profitable for banks with excess funds to lend to banks with deficits at market rates. Competition between banks with excess reserves for custom puts downward pressure on the short-term interest rate (overnight funds rate) and depending on the state of overall liquidity may drive the interbank rate down below the operational target interest rate. When the system is in surplus overall this competition would drive the rate down to the support rate.
The main instrument of this liquidity management is through open market operations, that is, buying and selling government debt. When the competitive pressures in the overnight funds market drives the interbank rate below the desired target rate, the central bank drains liquidity by selling government debt. This open market intervention therefore will result in a higher value for the overnight rate. Importantly, we characterise the debt-issuance as a monetary policy operation designed to provide interest-rate maintenance. This is in stark contrast to orthodox theory which asserts that debt-issuance is an aspect of fiscal policy and is required to finance deficit spending.
So the fundamental principles that arise in a fiat monetary system are as follows.
- The central bank sets the short-term interest rate based on its policy aspirations.
- Government spending is independent of borrowing which the latter best thought of as coming after spending.
- Government spending provides the net financial assets (bank reserves) which ultimately represent the funds used by the non-government agents to purchase the debt.
- Budget deficits put downward pressure on interest rates contrary to the myths that appear in macroeconomic textbooks about ‘crowding out’.
- The “penalty for not borrowing” is that the interest rate will fall to the bottom of the “corridor” prevailing in the country which may be zero if the central bank does not offer a return on reserves.
- Government debt-issuance is a “monetary policy” operation rather than being intrinsic to fiscal policy, although in a modern monetary paradigm the distinctions between monetary and fiscal policy as traditionally defined are moot.
Accordingly, debt is issued as an interest-maintenance strategy by the central bank. It has no correspondence with any need to fund government spending. Debt might also be issued if the government wants the private sector to have less purchasing power.
Further, the idea that governments would simply get the central bank to “monetise” treasury debt (which is seen orthodox economists as the alternative “financing” method for government spending) is highly misleading. Debt monetisation is usually referred to as a process whereby the central bank buys government bonds directly from the treasury.
In other words, the federal government borrows money from the central bank rather than the public. Debt monetisation is the process usually implied when a government is said to be printing money. Debt monetisation, all else equal, is said to increase the money supply and can lead to severe inflation.
However, as long as the central bank has a mandate to maintain a target short-term interest rate, the size of its purchases and sales of government debt are not discretionary. Once the central bank sets a short-term interest rate target, its portfolio of government securities changes only because of the transactions that are required to support the target interest rate.
The central bank’s lack of control over the quantity of reserves underscores the impossibility of debt monetisation. The central bank is unable to monetise the federal debt by purchasing government securities at will because to do so would cause the short-term target rate to fall to zero or to the support rate. If the central bank purchased securities directly from the treasury and the treasury then spent the money, its expenditures would be excess reserves in the banking system. The central bank would be forced to sell an equal amount of securities to support the target interest rate.
The central bank would act only as an intermediary. The central bank would be buying securities from the treasury and selling them to the public. No monetisation would occur.
However, the central bank may agree to pay the short-term interest rate to banks who hold excess overnight reserves. This would eliminate the need by the commercial banks to access the interbank market to get rid of any excess reserves and would allow the central bank to maintain its target interest rate without issuing debt.
The following blogs may be of further interest to you:
- The consolidated government – treasury and central bank
- Saturday Quiz – May 1, 2010 – answers and discussion
- Understanding central bank operations
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- Deficit spending 101 – Part 1
- Deficit spending 101 – Part 2
- Deficit spending 101 – Part 3
Premium Question 5:
The Eurozone countries will only start to reduce their public debt ratio when the respective governments succeed in running primary budget surpluses (that is, spending net of interest payments is less than taxation revenue).
The answer is False.
While Modern Monetary Theory (MMT) places no particular importance in the public debt to GDP ratio for a sovereign government, given that insolvency is not an issue, the mainstream debate is dominated by the concept. The unnecessary practice of fiat currency-issuing governments of issuing public debt $-for-$ to match public net spending (deficits) ensures that the debt levels will always rise when there are deficits.
But the rising debt levels do not necessarily have to rise at the same rate as GDP grows. The question is about the debt ratio not the level of debt per se.
Rising deficits often are associated with declining economic activity (especially if there is no evidence of accelerating inflation) which suggests that the debt/GDP ratio may be rising because the denominator is also likely to be falling or rising below trend.
Further, historical experience tells us that when economic growth resumes after a major recession, during which the public debt ratio can rise sharply, the latter always declines again.
It is this endogenous nature of the ratio that suggests it is far more important to focus on the underlying economic problems which the public debt ratio just mirrors.
The mainstream framework for analysing the dynamics in public debt ratios starts with the concept of the government budget constraint (GBC). The GBC says that the budget deficit in year t is equal to the change in government debt over year t plus the change in high powered money over year t. So in mathematical terms it is written as:
which you can read in English as saying that Budget deficit = Government spending + Government interest payments – Tax receipts must equal (be “financed” by) a change in Bonds (B) and/or a change in high powered money (H). The triangle sign (delta) is just shorthand for the change in a variable.
However, this is merely an accounting statement. In a stock-flow consistent macroeconomics, this statement will always hold. That is, it has to be true if all the transactions between the government and non-government sector have been correctly added and subtracted.
For a sovereign government that issues its own currency, the previous equation is just an ex post accounting identity that has to be true by definition and has no real economic importance.
However, for nations such as Greece, which has ceded its currency sovereignty, the GBC becomes an financial constraints given that it has to fund its spending from taxation and/or bond issues.
A primary budget balance is the difference between government spending (excluding interest rate servicing) and taxation revenue.
The standard mainstream framework is usually expressed in terms of the ratio of debt to GDP rather than the level of debt per se. Even so-called progressives (deficit-doves) use this framework as if it applies to all governments.
The following equation captures the approach:
![]()
So the change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP.
The real interest rate is the difference between the nominal interest rate and the inflation rate.
This standard mainstream framework is used to highlight the dangers of running deficits. But even progressives (not me) use it in a perverse way to justify deficits in a downturn balanced by surpluses in the upturn.
Many mainstream economists and a fair number of so-called progressive economists say that governments should as some point in the business cycle run primary surpluses (taxation revenue in excess of non-interest government spending) to start reducing the debt ratio back to “safe” territory.
Almost all the media commentators that you read on this topic take it for granted that the only way to reduce the public debt ratio is to run primary surpluses. That is what the whole “credible exit strategy” rhetoric is about and what is driving the austerity push around the world at present.
So the question is whether continuous national governments deficits imply continuously rising public debt levels as a percentage of GDP and whether primary budget surpluses are required to reduce the public debt ratio.
While MMT advocates running budget deficits when they are necessary to fill a spending gap left by non-government saving, it also emphasises that a government running a deficit can also reduce the debt ratio if it stimulates growth.
The standard formula above can easily demonstrate that a nation running a primary deficit can reduce its public debt ratio over time.
Furthermore, depending on contributions from the external sector, a nation running a deficit will more likely create the conditions for a reduction in the public debt ratio than a nation that introduces an austerity plan aimed at running primary surpluses.
Here is why that is the case. A growing economy can absorb more debt and keep the debt ratio constant or falling. From the formula above, if the primary budget balance is zero, public debt increases at a rate r but the public debt ratio increases at r – g.
The orthodox economists use this analysis to argue that permanent deficits are bad because the financial markets will “penalise” a government living on debt. If the public debt ratio is “too high” (whatever that is or means), markets “lose faith” in the government.
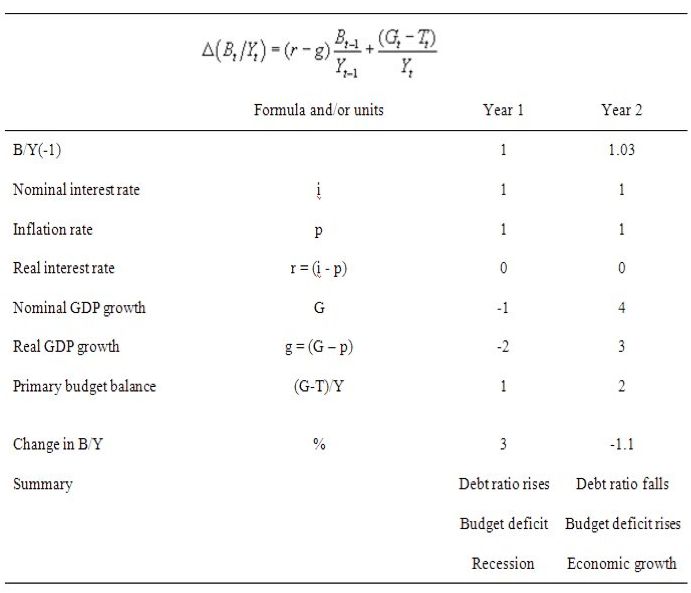
Consider the following Table which shows two years in the life of an economy.
It keeps things simple by assuming a public debt ratio at the start of the period of 100 per cent (so B/Y(-1) = 1).
Assume that the real rate of interest is 0 (so the nominal interest rate equals the inflation rate) – not to dissimilar to the situation at present in many countries.
Assume that the rate of real GDP growth is minus 2 per cent (that is, the nation is in recession) and the automatic stabilisers push the primary budget balance into deficit equal to 1 per cent of GDP. As a consequence, the public debt ratio will rise by 3 per cent. So in Year 2, the debt ratio is 1.03 of GDP.
The government reacts to the recession in the correct manner and increases its discretionary net spending to take the deficit in Year 2 to 2 per cent of GDP (noting a positive number in this instance is a deficit).
The central bank maintains its zero interest rate policy and the inflation rate also remains at zero so the real interest rate doesn’t move.
The increasing deficit stimulates economic growth in Year 2 such that real GDP grows by 3 per cent. In this case the public debt ratio falls by 1 per cent.
So even with an increasing (or unchanged) deficit, real GDP growth can reduce the public debt ratio, which is what has happened many times in past history following economic slowdowns.
In other words, a government such as Greece does not have to run budget surpluses to bring its public debt ratio down. What it needs is growth and that is more likely to occur if it holds its nerve and runs deficits. The problem is that the membership of the EMU (lack of currency sovereignty) makes that difficult without ECB support.
The best way to reduce the public debt ratio is to stop issuing debt. A sovereign government doesn’t have to issue debt if the central bank is happy to keep its target interest rate at zero or pay interest on excess reserves.
The discussion also demonstrates why tightening monetary policy makes it harder for the government to reduce the public debt ratio – which, of-course, is one of the more subtle mainstream ways to force the government to run surpluses.
The following blog may be of further interest to you:
About question 2, I think the explanation is insufficient. What Bill is saying is that, in the absence of paying banks extra interest in their reserves, the effective policy rate drops to zero, whatever the desired policy rate is (or depends on open market operations, per question 4). And the banks would not in that case hold excess reserves, but keep them at whatever statutory minimal level is set by law. That is all fine.
But in the current environment, the US Fed is paying interest on trillions of reserves it has stuffed into the banks, given them free income. Stopping that policy would seem to press banks to make more loans if they wanted future profits. Or charge more fees, or go out of business, etc. But giving the banks free money in this situation (when the policy rate is zero anyhow) would seem to a naive observer to enable them to survive without lending, and its reverse would encourage them to lend.
A reply might be that banks can lend in any case, and this alteration in their income would not affect their risk aversion and tendency to lend. But it would affect their need to lend as a source of income- i.e. to take risk that they otherwise shy away from.
Thanks!
With respect to Question 1: It seems to me that you have not answered the question that was asked but this depends on what you mean by the word “grow”. To me this refers to GDP.
Because GDP has the consumption C appearing in both the source and uses perspectives, it cancels out in the National Accounts Balance Equation (Let’s give this a name to enhance its profile). Hence, C can be increased without affecting the components of the national accounts and conversely the national accounts do not determine C necessarily, and hence the strict answer to the question if false.
It is true, though, that when we introduce behavioural laws, we would find some relation. For example, increasing a budget deficit by governent spending would be expected to be expansionary and would be inclined to increase consumption. If you allow this sort of argument, then the answer to the question might be true.
Banks in the U.S. cannot reduce their excess reserves. Only the Fed can do that. The only thing banks can do with their excess reserves is loan them to other baks who may need additional required reserves. The fed pays interest to keep the banks from offering a lower interest rate to other banks which would rive the rate toward zero.
Bill says in Q1 answer
“The general rule when the economy runs an external surplus is that the private domestic sector will be able to net save if the budget surplus is less than the external surplus.”
“That is why the external surplus is necessary but not sufficient. It relies on the budget surplus being large enough for the private domestic sector to be able to net save.”
The first statement makes the answer false as the question does not reference magnitudes. The second statement implies a large budget surplus enables the private sector to net save. Am I missing something?
Regarding:
“If the support rate is zero then persistent excess liquidity in the cash system (excess reserves) will instigate dynamic forces which would drive the short-term interest rate to zero unless the government sells bonds (or raises taxes). This support rate becomes the interest-rate floor for the economy.”
This seems technically true to me – raising taxes does drain liquidity – but is this really a practicable governmental policy for managing short-term interest rates? As I understand MMT, government bonds sales (and purchases) exert a near-instantaneous and easily observable effect on short term rates – from day to day or even hour to hour. Could any tax be that flexible? Or have I misunderstood the mechanism of bond purchases?
Cheers
Q1: doesn’t state nominal, so is not proved to be true, because most people assume we are interested in real growth unless otherwise specified.
Dear Frank Deliquo (at 2012/07/03 at 17:00)
Thanks for your comment.
The conclusions are independent of considerations regarding the deflator. An economy cannot grow in nominal or real terms if there is a net nominal spending drain.
best wishes
bill
Bill,
Neither the question nor the answer refers to “wage share”, “real wage” or “labour productivity”.
Dear Frank Deliquo (at 2012/07/04 at 10:12)
Sorry, I looked up the wrong quiz. I have edited my reply to you.
best wishes
bill
Bill,
Thanks for the edit.
“The conclusions are independent of considerations regarding the deflator”
Then the question is ambiguous. It needs to be changed to “nation wishes to achieve nominal growth”, for the answer to constitute a valid proof.
“An economy cannot grow in nominal or real terms if there is a net nominal spending drain.”
This requires a separate proof, as it is not covered in the answer.
Frank. Interesting blog. Think the question is even more about signs than the “relative magnitude of the sectoral balances”. (Cf Markg’s first objection above, though “but not sufficient” slips in a reference to relative magnitudes.)
Amounting to a statement that adding a positive number to a given negative number is a necessary but not sufficient condition for the result to be positive, or even more simply, that two negatives can’t sum to a positive, cf Bill’s reply.
Whatever happens, whether there is inflation or deflation, the deflator is going to be a positive number, so multiplying by it won’t change signs. So taking things in inflation-adjusted “real” or nominal terms is equally valid.
As Markg notes above, I think in there is a problem in Bill’s last sentence in his answer:
“It relies on the budget surplus being large enough for the private domestic sector to be able to net save.”
Should be “budget surplus being small enough”, or “external surplus being large enough” I think.
Would appreciate comment on what Tony says about “grow” & “C”.