Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – August 11, 2012 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you understand the reasoning behind the answers. If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
If the inflation rate is steady and the central bank maintains a constant nominal interest rate, then under current institutional arrangements where governments match deficit spending with debt issuance to the private sector, the public debt ratio will rise if the government deficit doubles (say, from 2 to 4 per cent of GDP).
The answer is False.
There are two concepts that are central to the question: (a) a rising budget deficit – which is a flow and not scaled by GDP in this case; and (b) a rising public debt ratio which by construction (as a ratio) is scaled by GDP.
The two concepts are not commensurate although they are related in some way.
A rising budget deficit does not necessary lead to a rising public debt ratio. You might like to refresh your understanding of these concepts by reading this blog – Saturday Quiz – March 6, 2010 – answers and discussion.
While the mainstream macroeconomics thinks that a sovereign government is revenue-constrained and is subject to the government budget constraint, MMT places no particular importance in the public debt to GDP ratio for a sovereign government, given that insolvency is not an issue.
The mainstream framework for analysing the so-called “financing” choices faced by a government (taxation, debt-issuance, money creation) – the government budget constraint – is written as:
Which you can read in English as saying that Budget deficit = Government spending + Government interest payments – Tax receipts must equal (be “financed” by) a change in Bonds (B) and/or a change in high powered money (H). The triangle sign (delta) is just shorthand for the change in a variable.
Remember, this is merely an accounting statement. In a stock-flow consistent macroeconomics, this statement will always hold. That is, it has to be true if all the transactions between the government and non-government sector have been correctly added and subtracted (accounted for).
From the perspective of Modern Monetary Theory (MMT), the previous equation is just an ex post accounting identity that has to be true by definition and has no real economic importance.
For the mainstream economist, the equation represents an ex ante (before the fact) financial constraint that the government is bound by. The difference between these two conceptions is very significant and the second (mainstream) interpretation cannot be correct if governments issue fiat currency (unless they place voluntary constraints on themselves to act as if it is).
That interpretation is inapplicable (and wrong) when applied to a sovereign government that issues its own currency.
But the accounting relationship can be manipulated to provide an expression linking deficits and changes in the public debt ratio.
The following equation expresses the relationships above as proportions of GDP:
The change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP. A primary budget balance is the difference between government spending (excluding interest rate servicing) and taxation revenue.
The real interest rate is the difference between the nominal interest rate and the inflation rate. If inflation is maintained at a rate equal to the interest rate then the real interest rate is constant.
A growing economy can absorb more debt and keep the debt ratio constant or falling. From the formula above, if the primary budget balance is zero, public debt increases at a rate r but the public debt ratio increases at r – g.
For example, if r = 0, and g = 2, the primary deficit ratio could equal 2 per cent (of GDP) and the public debt ratio would be unchanged. Doubling the primary deficit to 4 per cent would require g to rise to 4 for the public debt ratio to remain unchanged. That is entirely possible.
A nation running a primary deficit can obviously reduce its public debt ratio over time or hold it constant if growth is stimulated. Further, you can see that even with a rising primary deficit, if output growth (g) is sufficiently greater than the real interest rate (r) then the debt ratio can fall from its value last period.
Furthermore, depending on contributions from the external sector, a nation running a deficit will more likely create the conditions for a reduction in the public debt ratio than a nation that introduces an austerity plan aimed at running primary surpluses.
Clearly, the real growth rate has limits and that would limit the ability of a government (that voluntarily issues debt) to hold the debt ratio constant while expanding its budget deficit as a proportion of GDP.
The following blog may be of further interest to you:
Question 2:
The neo-liberal era has been characterised by a declining wage share in national income in many nations. This means that the real living standards of worker’s has been systematically eroded in these nations.
The answer is False.
The wage share is related to workers’ real living standards but does not define them.
The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.
To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.
Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.
The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.
So the wage bill = W.L
The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.
Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:
LP = GDP/L
so it tells us what real output (GDP) each labour unit that is added to production produces on average.
We can also define another term that is regularly used in the media – the real wage – which is the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).
We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.
The real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).
We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.
So the proposition in the question – that a declining wage share means the real standard of living for workers is falling – is false.
Irrespective of what happens to the wage share, as long as the real wage is rising, material standards of living will be rising (other things equal). That is, a declining wage share per se doesn’t denote a decline in workers’ living standards.
What it tells us is that a rising proportion of national income is going to profits (non-wages). But that rising proportion could be in relation to an overall expanding pie.
A declining wage share is consistent with growth in the real wage which is slower than the growth in labour productivity. If the real wage is growing but labour productivity is growing faster, then the wage share will fall.
A declining wage share driven by a real wage falling (and labour productivity at least not falling by as much) would signify a decline in living standards but that is because the real wage is falling.
The following blogs may be of further interest to you:
- The origins of the economic crisis
- Saturday Quiz – May 15, 2010 – answers and discussion
- Calling Planet Earth – they will print low
Question 3:
Real wages will rise if the rate of growth in nominal earnings outstrips the growth in labour productivity (output per unit of labour input).
The answer is False.
The question requires you to understand what determines the real wage and what the relationship between earnings and labour productivity growth is.
The real wage is defined as the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).
We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.
Macroeconomics is hard to learn because it involves these abstract variables that are never observed – like the price level, like “the interest rate” etc. They are just stylisations of the general tendency of all the different prices and interest rates.
Now the nominal wage (W) – that is paid by employers to workers is determined in the labour market – by the contract of employment between the worker and the employer. The price level (P) is determined in the goods market – by the interaction of total supply of output and aggregate demand for that output although there are complex models of firm price setting that use cost-plus mark-up formulas with demand just determining volume sold. We shouldn’t get into those debates here.
The inflation rate is just the continuous growth in the price level (P). A once-off adjustment in the price level is not considered by economists to constitute inflation.
So the real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).
We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.
The relationship between the real wage and labour productivity relates to movements in the unit costs, real unit labour costs and the wage and profit shares in national income.
The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.
To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.
Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.
The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.
So the wage bill = W.L
The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.
Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:
LP = GDP/L
so it tells us what real output (GDP) each labour unit that is added to production produces on average.
Nominal GDP ($GDP) can be written as P.GDP, where the P values the real physical output.
Now if you put of these concepts together you get an interesting framework. To help you follow the logic here are the terms developed and be careful not to confuse $GDP (nominal) with GDP (real):
- Wage share = (W.L)/$GDP
- Nominal GDP: $GDP = P.GDP
- Labour productivity: LP = GDP/L
- Real wage: w = W/P
By substituting the expression for Nominal GDP into the wage share measure we get:
Wage share = (W.L)/P.GDP
In this area of economics, we often look for alternative way to write this expression – it maintains the equivalence (that is, obeys all the rules of algebra) but presents the expression (in this case the wage share) in a different “view”.
So we can write as an equivalent:
Wage share – (W/P).(L/GDP)
Now if you note that (L/GDP) is the inverse (reciprocal) of the labour productivity term (GDP/L). We can use another rule of algebra (reversing the invert and multiply rule) to rewrite this expression again in a more interpretable fashion.
So an equivalent but more convenient measure of the wage share is:
Wage share = (W/P)/(GDP/L) – that is, the real wage (W/P) divided by labour productivity (GDP/L).
I won’t show this but I could also express this in growth terms such that if the growth in the real wage equals labour productivity growth the wage share is constant. The algebra is simple but we have done enough of that already.
That journey might have seemed difficult to non-economists (or those not well-versed in algebra) but it produces a very easy to understand formula for the wage share.
Two other points to note. The wage share is also equivalent to the real unit labour cost (RULC) measures that Treasuries and central banks use to describe trends in costs within the economy. Please read my blog – Saturday Quiz – May 15, 2010 – answers and discussion – for more discussion on this point.
Now it becomes obvious that if the nominal wage (W) and the price level (P) are growing at the pace the real wage is constant. And if the real wage is growing at the same rate as labour productivity, then both terms in the wage share ratio are equal and so the wage share is constant.
The wage share was constant for a long time during the Post Second World period and this constancy was so marked that Kaldor (the Cambridge economist) termed it one of the great “stylised” facts. So real wages grew in line with productivity growth which was the source of increasing living standards for workers.
The productivity growth provided the “room” in the distribution system for workers to enjoy a greater command over real production and thus higher living standards without threatening inflation.
Since the mid-1980s, the neo-liberal assault on workers’ rights (trade union attacks; deregulation; privatisation; persistently high unemployment) has seen this nexus between real wages and labour productivity growth broken. So while real wages have been stagnant or growing modestly, this growth has been dwarfed by labour productivity growth.
The following blogs may be of further interest to you:
Question 4:
When a nation runs a budget surplus it indicates that the national government is trying to slow the economy down and contain inflation.
The answer is False.
The correct answer would be that you cannot conclude anything about the government’s policy intentions from the budget outcome independent of other information.
The actual budget balance outcome that is reported in the press and by Treasury departments is not a pure measure of the fiscal policy stance adopted by the government at any point in time. As a result, a straightforward interpretation of the government’s discretionary fiscal intentions is not possible when using the actual reported budget outcome.
Economists conceptualise the actual budget outcome as being the sum of two components: (a) a discretionary component – that is, the actual fiscal stance intended by the government; and (b) a cyclical component reflecting the sensitivity of certain fiscal items (tax revenue based on activity and welfare payments to name the most sensitive) to changes in the level of activity.
The former component is now called the “structural deficit” (or surplus) and the latter component is sometimes referred to as the automatic stabilisers.
The structural deficit/surplus thus conceptually reflects the chosen (discretionary) fiscal stance of the government independent of cyclical factors.
The cyclical factors refer to the automatic stabilisers which operate in a counter-cyclical fashion. When economic growth is strong, tax revenue improves given it is typically tied to income generation in some way. Further, most governments provide transfer payment relief to workers (unemployment benefits) and this decreases during growth.
In times of economic decline, the automatic stabilisers work in the opposite direction and push the budget balance towards deficit, into deficit, or into a larger deficit. These automatic movements in aggregate demand play an important counter-cyclical attenuating role. So when GDP is declining due to falling aggregate demand, the automatic stabilisers work to add demand (falling taxes and rising welfare payments). When GDP growth is rising, the automatic stabilisers start to pull demand back as the economy adjusts (rising taxes and falling welfare payments).
The alternative is true when the economy is growing fast – tax revenue increases and welfare payments decline. So a budget may move into surplus even though the discretionary policy stance is expansionary. This would mean however that the overall budget impact is contractionary because the automatic stabiliser impact is overriding the discretionary intent.
The problem is always how to determine whether the chosen discretionary fiscal stance is adding to demand (expansionary) or reducing demand (contractionary). It is a problem because a government could be run a contractionary policy by choice but the automatic stabilisers are so strong that the budget goes into deficit which might lead people to think the “government” is expanding the economy.
So just because the budget goes into deficit doesn’t allow us to conclude that the Government has suddenly become of an expansionary mind. In other words, the presence of automatic stabilisers make it hard to discern whether the fiscal policy stance (chosen by the government) is contractionary or expansionary at any particular point in time.
To overcome this ambiguity, economists decided to measure the automatic stabiliser impact against some benchmark or “full capacity” or potential level of output, so that we can decompose the budget balance into that component which is due to specific discretionary fiscal policy choices made by the government and that which arises because the cycle takes the economy away from the potential level of output.
As a result, economists devised what used to be called the Full Employment or High Employment Budget. In more recent times, this concept is now called the Structural Balance. As I have noted in previous blogs, the change in nomenclature here is very telling because it occurred over the period that neo-liberal governments began to abandon their commitments to maintaining full employment and instead decided to use unemployment as a policy tool to discipline inflation.
The Full Employment Budget Balance was a hypothetical construction of the budget balance that would be realised if the economy was operating at potential or full employment. In other words, calibrating the budget position (and the underlying budget parameters) against some fixed point (full capacity) eliminated the cyclical component – the swings in activity around full employment.
This framework allowed economists to decompose the actual budget balance into (in modern terminology) the structural (discretionary) and cyclical budget balances with these unseen budget components being adjusted to what they would be at the potential or full capacity level of output.
The difference between the actual budget outcome and the structural component is then considered to be the cyclical budget outcome and it arises because the economy is deviating from its potential.
So if the economy is operating below capacity then tax revenue would be below its potential level and welfare spending would be above. In other words, the budget balance would be smaller at potential output relative to its current value if the economy was operating below full capacity. The adjustments would work in reverse should the economy be operating above full capacity.
If the budget is in deficit when computed at the “full employment” or potential output level, then we call this a structural deficit and it means that the overall impact of discretionary fiscal policy is expansionary irrespective of what the actual budget outcome is presently. If it is in surplus, then we have a structural surplus and it means that the overall impact of discretionary fiscal policy is contractionary irrespective of what the actual budget outcome is presently.
So you could have a downturn which drives the budget into a deficit but the underlying structural position could be contractionary (that is, a surplus). And vice versa.
The following blogs may be of further interest to you:
- A modern monetary theory lullaby
- Saturday Quiz – April 24, 2010 – answers and discussion
- The dreaded NAIRU is still about!
- Structural deficits – the great con job!
- Structural deficits and automatic stabilisers
- Another economics department to close
Premium Question 5:
Suppose that the government announced as part of a fiscal austerity strategy that it intended to cut its deficit from 4 per cent of GDP to 2 per cent in the coming year and during that year net exports were projected to move from a deficit of 1 per cent of GDP to a surplus of 1 per cent of GDP. In that situation we would not be able to conclude that the fiscal austerity plans would undermine growth if the net export projection was realised.
The answer is True.
This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.
From an accounting sense, if the external sector goes into surplus (positive net exports) there is scope for the government balance to move into surplus without compromising growth as long as the external position more than offsets any actual private domestic sector net saving.
In that sense, the EU/IMF/ECB strategy requires more than net exports adding as much aggregate demand as the government destroys with its fiscal austerity.
Skip the next section explaining the balances if you are familiar with the derivation. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced.
Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X – M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I – S) + (G – T) + (X – M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
- The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
- The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
- The Current Account balance (X – M) – positive if in surplus, negative if in deficit.
These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
If the nation is running an external surplus it means that the contribution to aggregate demand from the external sector is positive – that is net spending injection – providing a boost to domestic production and income generation.
The extent to which this allows the government to reduce its deficit (by the same amount as the move into external surplus) and not endanger growth depends on the private domestic sector’s spending decisions (overall). If the private domestic sector runs a deficit, then the fiscal austerity strategy will work under the assumed conditions – inasmuch as the goal is to reduce the budget deficit without compromising growth.
But this strategy would be unsustainable as it would require the private domestic sector overall to continually increase its indebtedness.
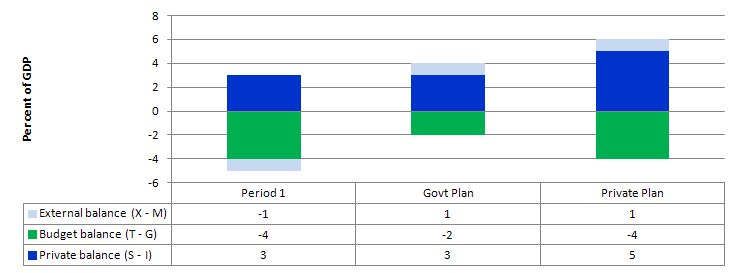
The following graph captures what might happen if the private domestic sector (households and firms) seeks to increase its overall saving at the same time the net exports are rising and the government deficit is falling.
In Period 1, there is an external deficit of 1 per cent of GDP and a budget deficit of 4 per cent of GDP which generates income sufficient to allow the private domestic sector to run a surplus (S – I > 0) of 3 per cent of GDP.
The Government plans to cut its deficit to 2 per cent of GDP by cutting spending. To achieve that with net exports rising to 1 per cent of GDP and for there to be no change in aggregate demand then the private domestic sector is assumed not to be changing its saving behaviour.
However, what happens if the private sector, fearing the contractionary forces coming from the announced cuts in public spending and not really being in a position to assess what might happen to net exports over the coming period, decides to increase its saving. In other words, they plan to increase net saving to 5 per cent of GDP – the situation captured under the Private Plan option.
In this case, if the private sector actually succeeded in reducing its spending and increasing its saving balance to 5 per cent of GDP, the national income shifts would ensure the government could not realise its planned deficit reduction.
The public and private plans are clearly not compatible and the resolution of their competing objectives would be achieved by national income shifts.
In other words, as the private sector and the public sector reduced their spending in pursuit of their plans, income would contract even though net exports were rising.
So unless private sector behaviour remains constant the government cannot rely on an increase in net exports to provide the space for them to cut their own net spending.
Thus, in general, with the government contracting the only way the private domestic sector could successfully increase its net saving is if the injection from the external sector offsett the drain from the domestic sector (public and private). Otherwise, income will decline and both the government and private domestic sector will find it difficult to reduce their net spending positions.
Take a balanced budget position, then income will decline unless the private domestic sector’s saving overall is just equal to the external surplus. If the private domestic sector tried to push its position further into surplus then the following story might unfold.
Consistent with this aspiration, households may cut back on consumption spending and save more out of disposable income. The immediate impact is that aggregate demand will fall and inventories will start to increase beyond the desired level of the firms.
The firms will soon react to the increased inventory holding costs and will start to cut back production. How quickly this happens depends on a number of factors including the pace and magnitude of the initial demand contraction. But if the households persist in trying to save more and consumption continues to lag, then soon enough the economy starts to contract – output, employment and income all fall.
The initial contraction in consumption multiplies through the expenditure system as workers who are laid off also lose income and their spending declines. This leads to further contractions.
The declining income leads to a number of consequences. Net exports improve as imports fall (less income) but the question clearly assumes that the external sector remains in deficit. Total saving actually starts to decline as income falls as does induced consumption.
So the initial discretionary decline in consumption is supplemented by the induced consumption falls driven by the multiplier process.
The decline in income then stifles firms’ investment plans – they become pessimistic of the chances of realising the output derived from augmented capacity and so aggregate demand plunges further. Both these effects push the private domestic balance further towards and eventually into surplus
With the economy in decline, tax revenue falls and welfare payments rise which push the public budget balance towards and eventually into deficit via the automatic stabilisers.
If the private sector persists in trying to increase its saving ratio then the contracting income will clearly push the budget into deficit.
So the external position has to be sufficiently strong enough to offset the domestic drains on expenditure. The answer is thus not clear.
The following blogs may be of further interest to you:
This Post Has 0 Comments