It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
Investment and interest rates
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text by the end of this year. Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.
Introduction to Cash Flow Discounting and Present Value
Investment and production decisions taken by firms are influenced by the expectations that entrepreneurs form about future revenue and cost streams which allow them to make guesses about what their profits might be.
Firms will try to formulate these expectations into specific cash flows and outlays across the time horizons that are appplicabe to the particular investment good. Different investment options will typically have different revenue and cost outlay profiles over time. So one piece of equipment might involve higher outlays in the more near future but deliver higher returns in a later period compared to another piece of equipment that delivers the same flow of production services but is cheaper in the near future but
In this section we introduce some introductory concepts to allow us to compare flows of funds between different periods in the future. The reason that this is not a straightforward exercise of su
Start with a rate of interest (the cost of obtaining funds) of 10 per cent. If you had $100 now and loaned it for a year then at the end of year 1 you would have $100 plus the interest earned which is given by the following formula:
(12.17) $100 + 0.10 x $100 = $100(1 + 0.10) = $110
This simple arithmetic generalises to the following model of compound interest:
(12.18) Pt+1 = Pt(1 + i)
where Pt+1 is the amount received in period t + 1 where t is now, Pt is the amount you invest now, and i is the nominal rate of interest.
What if you were to reinvest Pt+1 for the second year? You would expect to receive an amount Pt+2 according to the following formula:
(12.19) Pt+2 = Pt+1(1 + i)
From Equation (12.18) we know that Pt+1 = Pt(1 + i) so Equation (12.19) can be re-written as:
(12.20) Pt+2 = Pt(1 + i)(1 + i) = Pt(1 + i)2
We can generalise this if the period of the loan is n years to:
(12.21) Pt+n = Pt(1 + i)n
Equation (12.21) is a compound interest formula and assumes that the interest is added (compounded) at the end of each year. The formula gets more complicated if there are multiple compounding periods within the year. We do not consider these complications in this textbook.
You will appreciate from the concept of compound interest that a sum invested at a positive interest now will grow to a larger future nominal amount in the future. We can deploy this concept in reverse to calculate what a sum of cash that you expect to receive at some future date is worth today. You can see that this type of information is an essential component for a firm making investment decisions where the cash returns and outlays are received or incurred at some future date.
In general terms, how much would you have in today’s dollars if you knew you were to receive Pt+1 (that is, a sum of cash Pt+1 next year)?
From Equation (12.18) we can see that:
(12.22) Pt = Pt+1/(1 + i)
Consider our initial example where Pt+1 was $110 and i was 10 per cent. Equation (12.22) tells us that $110 received at the end of the year would be worth $100 now if the interest rate over the year was 10 per cent.
In this way, a firm can convert all future cash flows into current value using a generalised form of Equation (12.22).
You can think about this in this way. If you needed cash now and knew you were going to receive $110 at the end of this year and the current interest rate was 10 per cent then how much would you be able to sell your future claim on income for in the open market? The answer is $100 as long as the receipt at the end of the year was risk free and the inflation rate was zero (complications we will consider in a later Chapter).
No-one would be prepared to give you say $105 now in return for $110 at the end of the year if the interest rate was 10 per cent because they would be losing money. Similarly, you would be flooded with offers below $100 now if you were selling an asset (income flow) that would deliver the buyer $110 and interest rates were 10 per cent.
We also know that the current value of a future cash flow will be sensitive to the rate of interest. Imagine that the rate of interest was to fall during the year to 5 per cent. Then the future flow of cash of $110 would be worth $104.76 (110/(1+0.05)). You can verify that if you were to loan $104.76 now at 5 per cent then at the end of year 1 you would have $110. The future cash flow is less valuable now if the interest rate was to rise.
The current value of a future cash flow is called its present value (PV). The general formula for present value of a cash flow to be received at the end of period n is:
(12.22) Pt = Pt+n/(1 + i)n
What about the situation where the expected cash flows of varying are distributed across several different time periods? In that case, the present value of a flow at time t, Pt can be written as:
(12.23) Pt = Pt+1/(1 + i) + Pt+2/(1 + i)2 + Pt+3/(1 + i)3 + … + Pt+n/(1 + i)n
where the … refers to terms we have not written between time period t + 3 and n.
The conversion of disparate future cash flows across time into present values is generally called Discounted Cash Flow analysis.
Investment and the rate of interest
We are now in a position to consider the impact of the rate of interest on investment expenditure in more detail. As we learned in Chapters 7 and 8, investment decisions taken by entrepreneurs form an important component of total aggregate demand and income and as a result help explain changes in total employment.
Firms are continually making guesses about the future in terms of what the overall state of demand for their products will be, what they are likely to receive by way of revenue if their sales match these expectations, and what it will cost them to produce the output necessary to meet this demand.
Firms also have various choices about what products to produce and how they can produce them (for example, choice of technique). Firms are driven by the desire to make profit and will thus make choices among different types of productive equipment on the basis of which will contribute the most profit subject to a range of other considerations, many of which are subjective. For example, a firm that wishes to keep good standing in the community will probably eschew the use of equipment that is damaging to the local environment even if the use was legal and generated more profits than other options.
Whether firms use retained profits to fund future investment or seek funds from the markets there is a cost involved in purchasing new capital. A firm may have retained earnings to invest. It has the choice of investing them in new plant and equipment, or perhaps, purchasing financial assets which yield a positive rate of return (for example, a bond). While the firm will be driven by the need to stay in its present business and therefore defend its market share, which means it will usually want to use the funds available to it to purchase best practice, productive infrastructure; it may, at times, hold off from upgrading its productive capital if the circumstances are not conducive.
Investment decisions will thus depend on whether the productive asset being purchased delivers a positive return above the cost.
We can build on our understanding of present value (PV) to advance this idea in relation to the investment in productive capital.
Keynes and the Marginal Efficiency of Investment
In Chapter 11 The Marginal Efficiency of Capital of the The General Theory of Employment Interest and Money (published in 1936) John Maynard Keynes developed his theory of investment based in his concept of the Marginal Efficiency of Capital.
Keynes defined the Marginal Efficiency of Capital as:
… being equal to that rate of discount which would make the present value of the series of annuities given by the returns expected from the capital-asset during its life just equal to its supply price. This gives us the marginal efficiencies of particular types of capital-assets. The greatest of these marginal efficiencies can then be regarded as the marginal efficiency of capital in general.
His definition is difficult to understand and created some controversy, which we will touch upon here.
It is clear that he was thinking about two aspects of the investment decision: (a) the “prospective yield of the investment” which is a “series of annuities Q1, Q2, … Qn”. These are future flows of cash associated with an investment which the entrepreneur “expects to obtain from selling its output”. You can relate these flows to the earlier discussion of compound interest; and (b) the supply-price of the asset which he said was the “the price which would just induce a manufacturer newly to produce an additional unit of such assets” or in more simple language – “the replacement cost”.
The rate of discount he was referring to is also known as the internal rate of return of an project. As we saw in the last section, we can calculate a present value for any future cash flow stream. A net present value would be the present value of the revenue to be received minus the present value of the costs of the project.
A positive net present value coincides with a project that earns a positive rate of return in current dollars where a negative present value means that the project would lose money in current dollars.
The internal rate of return is the interest rate that would discount future income and cost outlays such that the net present value was zero.
Consider Figure 12.9 which provides data for a specific investment project. In the current year, the firm has to spent $10,000 to purchase the equipment. In subsequent years it receives the cash flows as indicated. We can assume there is no scrap value for the equipment after Year 5.
Figure 12.9 A Simple Cash Flow for an Investment Project
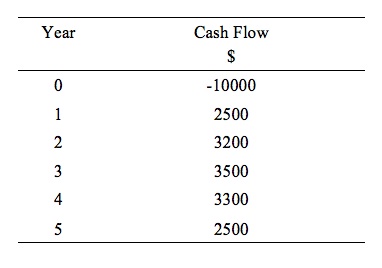
What is the internal rate of return (IRR) for this project?
The present value of the costs are $10,000 because they are all incurred in the current year (that is, now). The dollar sum of the cash returns is $15,000 but as we saw in the previous section, the dollar amounts cannot be compared across time periods because of the impacts of compounding.
The present value of the flow of revenue is given by the formula in Equation (12.23). Using the data in Figure 12.9 we would write this equation as:
(12.24) PV = $2,500/(1 + i) + $3,200/(1 + i)2 + $3,500/(1 + i)3 + $3,300/(1 + i)4 + $2,400//(1 + i)5
The internal rate of return is the discount rate (i)) that satisfies the following equation:
(12.25) NPV = -$10,000 + $2,500/(1 + i) + $3,200/(1 + i)2 + $3,500/(1 + i)3 + $3,300/(1 + i)4 + $2,400//(1 + i)5 = 0
The solution for i requires mathematics that are beyond the reach of this textbook (for interested students we have to solve the roots of Equation 12.25). You can use spreadsheet functions to do the task for you if you input the relevant data.
In our case, the IRR is 15.1 per cent.
You might like to input the data into a spreadsheet and compute the present value in Equation (12.24) using a discount rate of 15.1 per cent. You should verify that it equal to $10,000, which is exactly the present value of the initial outlay. The actual result you get may not equal $10,000 but this is due the approximate iterative solutions used by the spreadsheet.
This project will be profitable if the cost of borrowing funds to fund the project (that is, the market rate of interest) is below the IRR.
We can interpret Keynes’ concept of the MEC as being the return at the margin that a firm would expect to earn by investing in new capital equipment. That is, it is not the market return on existing assets.
Consider Figure 12.10 which shows three investment projects A, B and C that a firm has available to it ranked by their respective MEC. Project A has an IRR (or MEC) of 10 per cent, while Project B has an MEC of 8 per cent and Project C has an IRR of 5 per cent.
Figure 12.10 MEC and Investment Projects
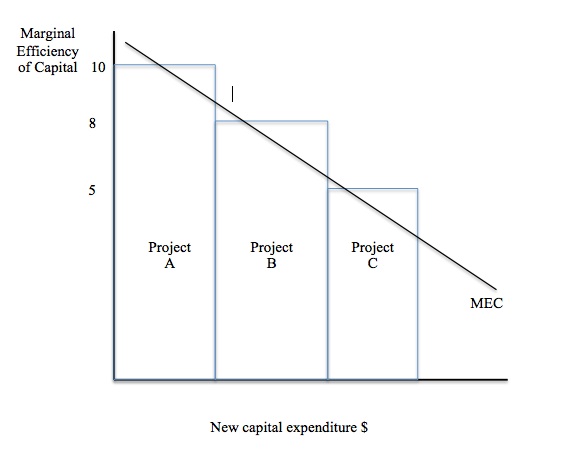
The firm must consider how much new capital expenditure it will incur for the coming year. If the market rate of interest is currently 9 per cent, then the firm would only be interested in investing in Project A, which means that its capital expenditure in the current planning period will be limited to Project A.
Should the market interest rate drop to below 8 per cent, then it will be profitable to borrow sufficient funds (or use retained earnings) and invest in both Project A and Project B. As a consequence total investment will rise. The firm will expand investment to Project C if the market rate of interest drops below 5 per cent.
The downward sloping MEC line that is depicted in Figure 12.10 summarises the investment response of the firm to changes in the market interest rate.
As a result a simple investment model of investment emerges whereby total investment in the economy is considered to be a downward function of the market rate of interest as in the Equation (12.25):
(12.25) I = I0 – bi
where I is total investment, I0 is some level of investment that is independent of the market rate of interest and b is the sensitivity of investment to the market rate of interest, i.
When considering Equation (12.25) you should always consider what lies behind it in terms of the MEC. The simple investment model, which says that rising market rates of interest lead to lower total investment is based on an assumption that all other things are equal. But as we have seen, underpinning the concept of the MEC is a comparison between the demand-side (expected revenue) and the supply-side (the replacement cost).
In a growing economy, it is likely that aggregate demand conditions will improve at times when the market rate of interest rises. The former will improve the revenue cash flows over time and increase the MEC for each project. In other words, we would not observe investment falling when the market rate of interest rose because the IRR of each project could also be increasing.
Thus it is important to avoid applying a mechanical interpretation of the concept of the MEC. Keynes, in fact, did not think investment would be very responsive to changes in the market rate of interest, especially when the economy was in recession or boom. Expectations formed by entrepreneurs underpinned their MEC calculations.
When the economy was in recession, entrepreneurs would become pessimistic and this would negatively impact on their assessment of the future returns from different projects. Further, with substantial excess productive capacity firms are unlikely to expand the capital stock even if new investment projects become cheaper as the central bank cuts the market interest rate to stimulate demand.
The extreme optimism that typically accompanies a boom also would reduce the sensitivity of investment to changes in the market rate of interest. With expected returns high, firms will be prepared to pay higher borrowing costs.
We could express this enhanced optimism by a shift outwards in the MEC line in Figure 12.10 which would make more Projects worth pursuing at a given market rate of interest.
If entrepreneurs became excessively pessimistic then the MEC line would shift inwards and fewer projects would be deemed profitable at a given market rate of interest even if the technical aspects of the equipment was unchanged.
For Keynes then, investment was a very subjective act and responsive to how firms felt about the economy. Even though Equation (12.25) seems simple the ideas underpinning it were anything but.
We consider the crucial role of expectations and what factors firms might consider when forming expectations of future returns in Chapter 17 Keynes and Classics and modern variants.
The concept of the MEC was refined by later economists including Abba Lerner who preferred the term Marginal Efficiency of Investment (MEI).
There were many criticisms of this approach to investment theory
A substantial criticism focused on the logic of a downward sloping MEC line at times when involuntary unemployment was observed. If we consider the expenditure multiplier, then aggregate demand rises by some multiple of a rise in investment expenditure and output rises.
If the MEC is influenced by expected future returns then the increased national income arising from the increased investment would logically lead to higher expected future revenue. In that case, the MEI will shift outwards as not above which means that investment should increase as a result. This would then stimulate further multiplied increases in aggregate demand and output and so the process would continue.
With plenty of excess capacity in the form of high unemployment, it is easy to conceive of a situation where investment would be indeterminate as the multiplied income increases feedback into further investment as expected returns improve. As a consequence, the firms will progressively invest in an increasing number of projects and the market interest rate would lose all relevance.
Once again we see the importance of expectations in this approach to investment.
The response to this criticism was also varied.
One approach attacked the idea that the MEI line could be aggregated across all firms to become the aggregate (or macro) investment function. It was argued that this “aggregate” investment line would over-estimate the investment that would accompany a fall in interest rates. The argument noted that if the interest rate was to fall and borrowing costs for all firms were now lower, then as all firms expanded investment in productive capacity, the rising demand for capital goods would drive their price up which would reduce the MEC lines for all firms.
Some economists have attempted to distinguish the MEC from the MEI along these lines, saying that the MEI is the relationship between total investment and market interest rates when the demand effects on the price of capital goods is taken into account.
Michel Kalecki introduced what he termed the Principle of Increasing Risk which brought together the investment decision and the risk of increased indebtedness that firms would carry as they expanded investment. As firms extended their exposure the success of the marginal projects in terms of generating realised returns became more crucial. Kalecki argued that firms would become increasingly risk averse as their debt levels rose and this would be expressed by more sobre expectations of the future returns from various projects.
Kalecki thus considered that increasing risk would thus ensure that the MEI was downward sloping with respect to the market rate of interest.
[NOTE: MORE TO COME ON THIS]
Alternative Olympic Games Medal Tally
My Alternative Olympic Games Medal Tally is now active.
I update it early in the day and again around lunchtime when all the sports are concluded for the day.
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
That is enough for today!
(c) Copyright 2012 Bill Mitchell. All Rights Reserved.
The answer is $110 as long as the receipt at the end of the year was risk free and the inflation rate was zero
Should be 100, shouldn’t it?
Dear Matthias (at 2012/08/10 at 21:40)
Yes, thanks for spotting the typo. Fixed now. Appreciated.
best wishes
bill
Not that important but Kalecki was Michał, not Michel.
It’s nice to know that some of the Microeconomics I learned 30 years ago still make sense.
Shame about the Macro
“(12.24) PV = $2,500/(1 + i) + $3,200/(1 + i)2 + $3,500/(1 + i)3 + $3,300/(1 + i)4 + $2,400//(1 + i)5
The internal rate of return is the discount rate (i)) that satisfies the following equation:
(12.25) NPV = -$10,000 + $2,500/(1 + i) + $3,200/(1 + i)2 + $3,500/(1 + i)3 + $3,300/(1 + i)4 + $2,400//(1 + i)5 = 0
The solution for i requires mathematics that are[is] beyond the reach of this textbook (for interested students we have to solve the roots of Equation 12.25). You can use spreadsheet functions to do the task for you if you input the relevant data.”
There’s nothing specially difficult about the mathematics here. There is no exact formula or algorithm for the roots of the polynomial in equation 12.25 so you have to use a numerical method. Since NPV is monotonically decreasing as i increases in the relevant range 1 + i > 0 and NPV is positive for i = 0 and clearly negative for sufficiently large i, there is one and only one solution to the equation in that range. A very simple way to find the solution accurately enough is to use a spreadsheet to calculate all values over a suitable range to find where NPV changes sign. Alternatively you could use a solve function in the spreadsheet or use some sort of Newton/gradient method but that would be overkill unless you wanted the solution accurate to umpteen decimal points.
RE: Alternative Olympic Medal Tallies
Rating by GDP per Capita is more likely to represent some removal of pure population and pure GDP factor advantages. What it then might suggest is that nations which win on this ranking are the ones that spend more on sport relative to their $PPP 1000 per person ranking. Either that or it suggests better efficiency and/or better adaptation of the populace to olympic sports on average. It could suggest a mix of all three of course.
The question of existent adaptations being suited to sport (on a sport specific basis) might get touchy but it has considerable empirical support. On average the saying “white men can’t run or jump” is correct. It could be expanded and refined to “caucasians aren’t quite as well adapted to pure running or jumping endeavours as some other groups are”. It is now relatively rare for caucasians to win running and perhaps even jumping sports at the Olympics. It seems clear to me that fortuitous genetic adaptation is playing a role. Adaptations due to earlier epoch natural selection pressures are involved.
Results in swimming might suggest white and northern asian people are more “adapted” to swimming but this conclusion is perhaps doubtful for two reasons. One, swimming in homo sapiens is not innate or instinctual, it is learned. Water is not our natural element and as a species we show little sign of being “dual-adapted” to land and water movement (unlike many reptiles for example). Thus swimming results are more likely to reflect culture, money, lifestyle and training advantages. However, cold adaptation in white and some Asian peoples might result in slightly higher natural buoyancy, even in fit individuals, due to slightly higher natural fat levels. The buoyancy suit fiasco showed incremental buoyancy advantages do play a role.
The ultimate question is what does modern sporting competition mean? The answer is that it means nothing outside of narcissistic competitiveness, narcissistic self image and nationalistic jingoism. Those people most gifted by social standing, wealth, opportunity, genetic endowment and work-willingness win. Each on its own is a necessary but not sufficient condition.
When all factors are taken into account, human individual agency is of vary little account in human outcomes. Winners deserve no praise and losers deserve no condemnation.
I applaud you sir.
What is the diffrence between PV and MEI as investment criteria