It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
Aggregate demand – Part 4 (redux)
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text by the end of this year. Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.
Note – this is a re-edit of the first three parts to better organise the pedagogy and to clear up some uncertainties (in my mind).
Chapter 8 Expenditure, output and income and the multiplier
8.1 Introduction
In Chapter 7, we introduced the concept of effective demand, within the original aggregate supply-aggregate demand framework (D-Z) developed by Keynes in the General Theory. Recall that Keynes defined the aggregate supply price of the output derived for a given amount employment as the “expectation of proceeds which will just make it worth the while of the entrepreneur to give that employment” (footnote to Keynes, J.M. (1936) The General Theory of Employment, Interest and Money, Macmillan, page 24 – check page).
We learned that this concept related a volume of revenue received from the sale of goods and services to each possible level of employment. At each point on the aggregate supply price curve, the revenue received would be sufficient to cover all production costs and desired profits at the relevant employment level.
The other way of thinking about the aggregate supply price Z-function is to express it as the total amount of employment that all the firms would offer for each expected receipt of sales revenue from the production that the employment would generate.
The important point here is that the relationship was expressed in terms of employment and the revenue expected to be received at each output level. We should be clear that Keynes was considering aggregate supply in terms of the expectation of proceeds, which is the money income (revenue) that the firms expect to get from selling their output. Firms are thus considered to formulate plans to gain a volume of money or nominal profits.
Why did he choose to employment instead of output itself? The reason relates to the developments in statistical gathering in the period that he was developing his theory (published 1936). National Accounting as we know it today (analysed in Chapter 5) did not exist in 1936. There were no reliable estimates of output (real GDP) but estimates of total employment were more accurate and more readily available.
It is for that reason that Keynes used employment instead of output as his measure of aggregate activity.
In this Chapter, we thus have two tasks. First, to express the model developed in Chapter 7 in terms of output rather than employment. Second, to consider total expenditure in real terms and relate that to a simple model of aggregate supply. In Chapter 9 we will complete the picture by developing a more detailed aggregate supply framework.
There are two aspects to conceiving of the income-expenditure framework in real terms. First we consider that when they spend, consumers, firms and governments desire to achieve real outcomes in terms of the command on real resources (output). So when a household is spending, for example $100 on consumption goods they are making a decision to purchase a real quantity of goods and services.
Second, to overcome the fact that the aggregate supply approach developed in Chapter 7 was cast in money (nominal) terms (revenue or proceeds) we need to recast the supply-side in real terms to render it consistent with the demand side.
We can do that by using the National Accounting concept of GDP at constant rather than current prices as our measure of economic activity. In other words, we are considering that firms cast their price and output decisions based on expectations of aggregate spending in order to achieve a real return over costs.
In this way, we do not diminish the importance of expectations in driving production and supply decisions by firms but we abstract from price changes and assume that firms react to changes in aggregate spending by adjusting the quantity of output rather than the price and quantity.
In other words, we adopt, for the time being, the assumption that firms are quantity adjusters, which means they respond dollar-for-dollar to increased demand by increasing output and income. There are various ways in which we can justify considering firms to be quantity adjusters.
First, we might assume that, typically, firms maintain some excess capacity and can thus increase output relatively easily without further investment in productive capacity.
Second, firms use mark-up pricing, whereby they add a profit mark-up to their unit costs and face roughly constant unit costs over the output range they normally produce within.
Third, firms face various costs in adjusting prices and as a result only periodically make such adjustments. It has been said that firms use “catalogue pricing”, whereby they make their prices known to their prospective customers through advertising and other means and then stand ready to sell goods and services at those prices irrespective of demand (up to their full productive capacity). At the end of the current catalogue period, they will then make any necessary adjustments to prices based on expected future demand and expected movements in unit costs.
We consider mark-up pricing models in more detail in Chapter 9 when we develop the detailed aggregate supply framework.
In terms of advancing a theory of employment, we now need to consider an employment requirements function, which relates the output that firms expect to sell (and therefore produce) to employment via a productivity relationship. If we know how many employment units are required to produce one unit of real output then once we know the sum of the firm’s production plans then we also will know the aggregate or macroeconomic demand for labour.
Employment can be measured in terms of hours worked or persons employed but in this Chapter we abstract from that issue. In Chapter 10 we consider the implications of how employment is measured when we formally introduce the labour market.
8.2 Aggregate Supply
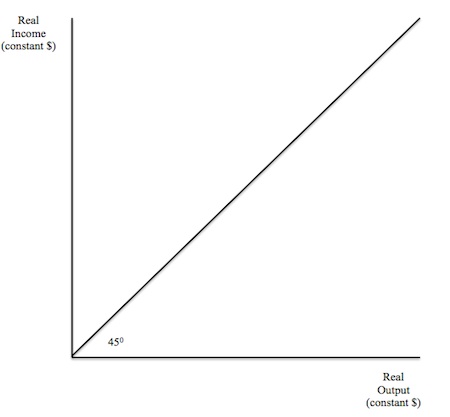
Figure 8.1 depicts the simplified constant price aggregate supply relationship that we will work with in this Chapter to concentrate on the way the economy adjusts to changes in aggregate demand. It is drawn as a 450 line emanating from the origin with total revenue (in constant dollars) on the vertical axis and real output on the horizontal axis.
Obviously, without considering any economic meaning, the 450 line shows all points where real income (real expected proceeds) is equal to real output. Given that real expected proceeds and real income is equal to real expenditure then the 450 line shows all points where output and expenditure are equal (in constant prices).
But consider what the 450 line implies with respect to postulated firm behaviour.
Think back to Chapter 5 when we explained the different perspectives that we can take in measuring aggregate economic activity. The expenditure, income and output approaches provided different views of the national accounting framework but in the end all yielded the same aggregate outcome. The total value of goods and services produced in any period was equal to the total spending and the total income generated (wage and other costs and profits) in that same period.
As we will see in Chapter 9 when we consider aggregate supply in more detail, total output (measured in Figure 8.1 along the horizontal axis) is exactly equal to total input costs (incomes to suppliers of labour and other productive materials) and profits.
In that context, firms will supply that output (and incur those costs) as long as it can generate enough revenue to cover the costs and realise its desired profits.
The vertical axis provides a measure of total expenditure which also equals to real income. From the perspective of the firms the vertical axis tells it the real expected proceeds that it can generate by selling the different levels of output.
It is in this way that we can conceive of the 450 line as the aggregate supply curve (in constant prices). At each point the firms are realising their expectations and ratifying their decision to supply real output to the market. The ratification comes through the receipt of expected income that covers both their costs in aggregate and the desired volume of profits.
The other point to note is that we have imposed no full capacity point on the graph. At some point, when the economy is operating at full capacity, firms are unable to continue expanding real output in response to additional spending. When we introduce the expenditure side of the economy in the next section we will also impose a full employment output condition beyond which firms cease to be quantity adjusters.
A diversion into employment
Before we consider the introduction of aggregate demand or expenditure into the model we will briefly show how this conception of aggregate supply based on expected proceeds translates into employment, given that we have real output on the horizontal axis now instead of employment.
We will deal with this question in detail in the next chapter but for now we introduce the concept of the Employment-Output function or the Employment Requirements Function, which shows the how much labour is required to produce a given volume of real output.
Firms hire labour to produce output. How much labour a firm hires will then be determined by how the productivity of labour and how much output the firm plans to produce in response to its expected demand for that output.
The employment-output function is expressed as:
(8.1) Y = αN
where N is the total number of workers employment, α is the rate of labour productivity, and Y is planned output (based on expected spending), which is equal to the actual income generated in the current period.
Firms make decisions to produce goods and services based on expected demand for such output and once all the sectors have made their spending decisions (that is, once aggregate demand is actually realised), the firms discover whether their expectations were accurate or not. That is, they discover whether they have overproduced, under-produced or produced according to the total realised spending.
Labour productivity is defined as output per unit of labour input. So we could solve Equation 9.1 for α to get Y/N, which is the algebraic equivalent of our definition.
The higher is labour productivity (α) the less employment is required to produce a unit of output for a given production technique (implicit in α).
In Chapter 9, we will discuss the factors which influence the magnitude of α.
For now, if α is stable in the short-run (within the current investment cycle) then once the firm decides on the level of output to produce, to satisfy expected demand, it simultaneously knows how many workers must be employed.
As an example, if it takes 10 workers to produce $1000 worth of output per day, then daily labour productivity would be $100 per worker. So if the firm anticipated an increase in output to say $1500 per day, they would require an additional 5 workers to ensure they could supply the new higher level of output.
Figure 8.2 ties the Aggregate Supply Function (depicted in Figure 8.1) together with the Employment-Output function. The upper panel is just a repeat of Figure 8.1. The lower left-hand panel has no other purpose other than to map the horizontal axis in the top panel into the vertical axis in to the lower right-hand panel (which we have now called the Employment-Requirements Function). The slope of the Employment-Requirments Function is the current labour productivity (α).
So if firms are happy based on their expectations to produce output at point A, then we can trace that level of output down to determine the employment level that would be required to produce that level of output at the current value of α.
If there are no other changes, then if firms believe they can sell more output than before (say at point B) then this will necessitate a rise in employment, which is shown in the lower right-hand panel as point B. We can say the Employment-Output Function provides tells us the total employment requirements for any given level of output.
We will examine the Employment-Output Function in more detail in Chapter 9.
Figure 8.2 Aggregate Supply and Employment requirements

[NOTE: Remember the diagrams will be professionally drawn]
Clearly the story is missing one vital element – what determines whether Point A or B or any other is the level of output actually produced in any given period?
For this we need to build a model of expenditure – that is, the Aggregate Demand Function.
By adding aggregate demand to the framework, we can then determined what we will call the equilibrium national output and income (the point of effective demand). At the equilibrium point, we will have determined three key macroeconomic aggregates – total expenditure (aggregate demand), total output (aggregate supply) and total employment.
Aggregate Demand
In Chapter 7, we learned that firms build a stock of productive capital through investment in order to produce goods and services to satisfy demand. One the capital stock in in place, firms will respond to increases in spending for the goods and services they supply by increasing output up to the productive limits of their capital and the available labour and other inputs. Beyond full capacity, they can only increase prices when increased spending occurs.
By adopting the assumption in this chapter that prices do not adjust to changes in demand, we thus say that higher aggregate demand will lead to increased production, which in turns increases national income.
Later in the chapter we will see that for an additional increase in national income, further positive demand effects follow, which, in turn, lead to further increases in real GDP.
Accordingly, if an economy enjoys a increase in aggregate demand (say, an increase in government spending) then that initial increase in output and income is multiplied throughout the economy. We will also learn that the multiplier also operates when there is a decline in aggregate demand. So recessions can quickly occur if a key component of aggregate demand declines and the initial lost output and income leads to subsequent spending cuts elsewhere in the economy.
The basic macroeconomic rule when there is productive capacity available is the spending drives output and national income which, in turn, drives employment.
For this purpose we are assuming that potential output is fixed for the period we are analysing. We will show that investment builds new capital and population growth adds new workers to the economy both of which expand potential output over time. In Chapter 12 we will consider economic growth and examine how aggregate demand and potential output can move over time.
We will learn that even if aggregate spending might currently be sufficient to maintain the full employment of available labour, growth in the supply-side of the economy – that is, potential output – will require ever more growth in aggregate demand in the future. In effect, with on-going investment, the economy chases itself to maintain full employment.
But for now we assume that potential output is fixed and that firms supply up to that potential according to the aggregate spending that prevails in any period.
The task of this section is to examine in more detail the components of total spending and explain how they interact to determine total output (GDP) and national income.
In Chapter 5 we introduced the National Accounting framework used by national statistical agencies and learned that total expenditure in any period is expressed as the sum of the following sources of spending:
- Consumption by households or persons (C)
- Investment spending by firms (I)
- Government spending (G)
- Export spending by foreigners (X) minus import spending by domestic residents (M), which we denote as net exports (NX) = (X – M).
In Chapter 5, the sum of these expenditure components equalled GDP as a matter of accounting. Total expenditure summed to total output and total income.
In the remainder we explore what factors determine each of these components of aggregate demand and how these interact to determine total income. We will also derive an expression for equilibrium national income which is a conceptual state that exists when the level of aggregate demand is stable.
From the National Accounting framework we know that total expenditure (E) in the domestic economy in any particular period can be expressed as:
(8.2) E = C + I + G + (X – M)
You will see that while exports add to total spending in the domestic economy, imports lead to a drain in spending because it comprises local residents, firms and governments spending on goods and services produced by other nations.
The equilibrium level of real national income (Y) is determined by aggregate demand (as long as prices remain unchanged).
(8.3) Y = E
You should note that the level of real GDP that is produced by the current period’s expenditure does not necessarily have to equal the full employment output level. Keynes among others demonstrated that it such an equality would be coincidental and that full employment was not guaranteed by the market system.
We consider those issues in detail in Chapter 10 when we study the labour market.
We now turn to developing an understanding of the behaviour of each of these expenditure components and how they interact in a simple income-expenditure model.
Private Consumption Expenditure
In Chapter 3 we discussed the role of government and the concept of money and learned that in a fiat-currency system the government issues the currency which the non-government sector uses. This gave us a very advanced understanding of how financial assets can enter the economy – with government at the centre of the stage.
In seeking an understanding of the determinants of aggregate demand we also have to focus on private sector decision-making which occurs within the broad set of constraints provided by the interaction between government and non-government.
Private consumption spending is the largest component of aggregate demand in most economies. Consumption is the sum of household spending on non-durables goods (for example, food), durable goods which provide benefits beyond a single year (for example, cars, white-goods) and services (for example, restaurants, theatres and the like).
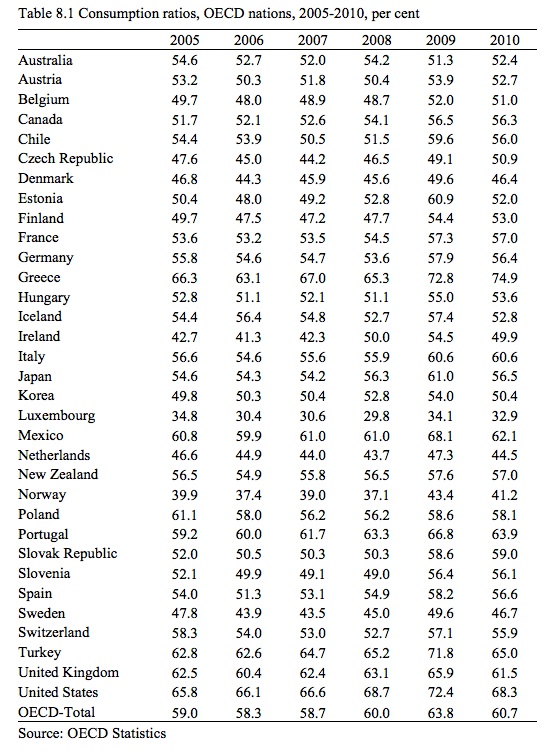
Table 8.1 shows the proportion of Private consumption expenditure in GDP for the OECD nations less Israel. While there are notable exceptions, most nations are around the OECD average of 60.7 per cent. Private consumption expenditure is the largest component of total spending on GDP. The ratio is also relatively stable over time.
Note that this Table shows the ratio of consumption to total GDP. In the next section we will relate total consumption spending to what economists call disposable income, which is total income (Y) less the amount that governments take out in the form of taxes (T).
What determines private consumption expenditure?
The most elementary theory of private consumption (C) says that it is a stable function of disposable national income (Yd). Disposable income is the volume of income that is left after the government has taken out taxes.
We define disposable income as:
(8.4) Yd = Y – T
A simple model of the government’s tax policy assumes that it levies a proportional tax rate (t) from total national income, which means that the total tax revenue (T) in any particular level of income is given as:
(8.5) T = tY
Assume that the proportional tax rate (t) is 0.20. This means that for every dollar of national income generated the government takes 20 cents out in the form of taxation. The remaining 80 cents in left over as disposable income.
We consider taxation to be a “leakage” from the expenditure system because it is income that is not available for private spending.
Given that taxes are taken out of total income (Y), disposable income can be written as:
(8.6) Yd = Y – T = Y – tY – (1-t)Y
In our specific example, this would be written as Yd = (1 – 0.2)Y = 0.8Y.
We conjecture that total consumption in the economy (C) is given as:
(8.7) C = C0 + cYd
C0 is some constant and is a base level of consumption which is independent of disposable income. The coefficient c is called the marginal propensity to consume (MPC) and measures the fraction of every dollar of disposable income that is consumed.
The MPC has a value between 0 and 1. If, for example, c = 0.8 then for every extra dollar of dispoable income that the economy generates consumption would rise by 80 cents.
It is important to understand that the MPC in this model is an aggregate which is an average of all the individual household consumption propensities. Lower income households tend to have MPC values close to 1 whereas the higher income households have much lower than average consumption propensities.
This arises because lower income families find it harder to purchase enough goods and services to maintain basic survival given their income levels. Higher income earners not only consume more in absolute terms but have more free income after they have purchased all the basic essentials.
As we will learn later in this chapter, the distribution of income is an important consideration when seeking to understand changes in aggregate demand. For example, a change in tax policy that increased disposable income for low-income consumers would have a greater positive impact on final consumption that a tax cut aimed at giving high-income earners the same absolute increase in disposable income.
In macroeconomics, the aggregate consumption function is defined as a relationship between total consumption (C) and total national income (Y).
We can find this relationship by substituting the expression for disposable income in Equation (8.6) into the consumption equation (8.7). The consumption function is thus written as:
(8.8) C = C0 + cYd = C0 + c(1 – t)Y
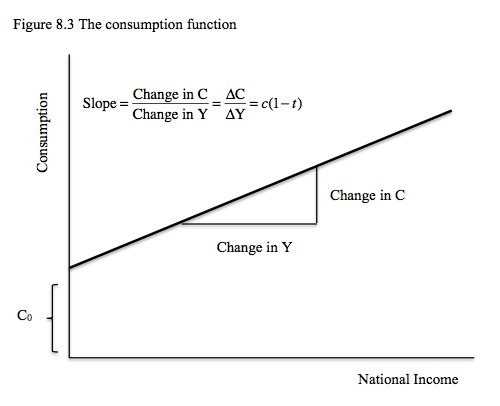
Figure 8.3 shows the consumption function in graphical terms.
The consumption function cuts the vertical axis at C0 > 0. The consumption function is then upward sloping because we have postulated that consumption rises with national income.
In Chapter 4 Methods, Tools and Techniques we learned how to derive a slope graphically. We said that the slope of a line is the ratio RISE over RUN. Rise in this case is the change in consumption spending (ΔC) and run is the change in national income (ΔY) and we have drawn a little triangle underneath the consumption function to show that.
In fact, ΔC = cΔY and RISE over RUN = ΔC/ΔY or c(1 – t)ΔY/ΔY = c(1 – t). The slope of the consumption function is thus given by the coefficient c(1 – t), which is is lower than the MPC because a $1 rise in national income translates into less than a $1 rise in disposable income given that the marginal tax rate (t) is positive
You should be able to work out what would happen if the MPC (c) increased? The result would be an increase in the slope of the consumption function such that at every level of disposable income, total consumption would be higher.
What determines aggregate saving (S)?
The difference between consumption (C) and disposable income is private saving (S), which can be written as:
(8.9) S = Yd – C = Y – T – C
Saving at the macroeconomic level is thus a residual that remains after households have made their consumption choices.
If the MPC or c is the proportion of disposable income that is consumed then we can define a related concept – the marginal propensity to save (s) which is just the 1 minus the marginal propensity to consume (c).
Both aggregate saving and consumption rise with national income. When national income rises, the government taxes out some taxes leaving an increase in disposable income which is then the source of increased consumption (via the marginal propensity to consume) with the remainder of the increase in disposable income being saved.
If the MPC is 0.8 and the tax rate is 0.2, then if national income increases by $100, total tax revenue rises by $20, disposable income rises by $80, consumption rises by $64 and $16 is saved.
The higher is the level of GDP for a given tax regime, the higher will saving and consumption will be. If households decide to increase the proportion of disposable income that they save, then the MPC will fall and aggregate demand will be reduced at every national income level because consumption will fall.
We will trace through the implications of these changes later in the chapter.
Introducing Private investment
When a macroeconomist uses the term investment they are referring to a very specific type of spending, which does not accord with the common usage of the term. For example, a lay person might think of investment as a person putting some money in a fixed-term deposit at a bank or the purchase of some shares in a company.
The National Accounting meaning of investment is any spending that adds to the productive capacity of the economy – or adds to the capital stock. Capital in this context is productive plant and equipment or other capacity which defines the potential output of an economy.
When a firm builds a new factory or purchases a new piece of machinery they are considered to be investing.
Inventories, which are unsold goods, are also considered to be a component of business investment in each period because they add to the potential of the economy to meet current aggregate demand for goods and services. As we will see, the dynamics of inventories provide important information about the state of the business cycle.
[NOTE: BRIEF DISCUSSION OF VOLATILITY AND INVESTMENT RATIOS HERE]
Economists distinguish between gross and net investment. Gross investment is the total spending by firms on firms on plant and equipment, constructions associated with productive capacity and inventories.
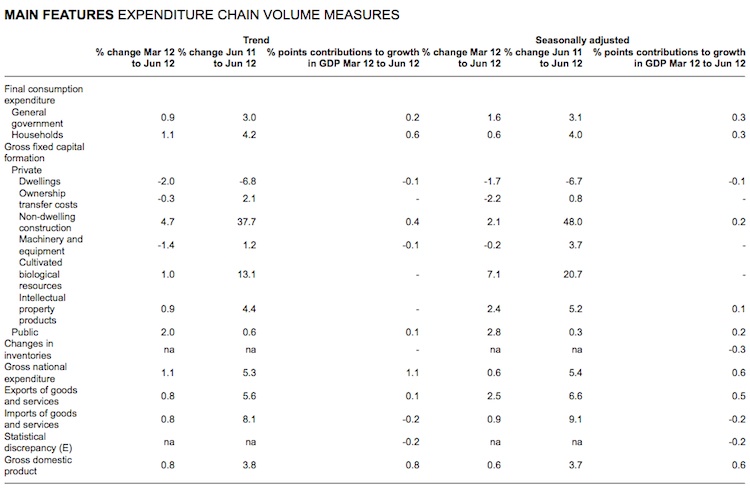
Figure 8.4 shows a snapshot of the Australian National Accounts for the June quarter 2012. The organisation of the expenditure components is based on the standard National Accounts framework that we discussed in Chapter 5, which is broadly shared across the world.
Under Gross fixed capital formation, a number of individual line entries are listed which comprise the separate categories within which the statistician estimates investment spending. Note that the statistician classifies the Change in inentories as a separate category.
Figure 8.4 Expenditure Components in National Accounts
However, in each period the existing capital stock depreciates. For example, machines wear out and/or become obsolete; buildings require maintenance; and car fleets require updating.
Some of the gross investment in each period merely covers the depreciation of the existing capital stock.
Net investment is the component of gross investment that adds new productive capacity – that is, which increases the overal capital stock.
Net investment is thus gross investment less total depreciation.
In Chapter 12, we will consider the determinants of private investment in detail. For now we assume that firms plan a fixed volume of investment spending in each period, I. We assume there is no depreciation of existing capital stock and no inventories.
Introducing Government spending
We have already introduced one element of the government’s interaction with the non-government sector – the proportional tax rate (t)
The National Accounts framework shows that government spending takes a variety of forms. First, all levels of government purchase a range of goods and services from the non-government sector as a means of fulfulling their social and economic goals. Some of the purchases are for consumption goods and services, while other spending is categorised as public investment or public capital formation. The latter category of spending generates the valuable public infrastucture that enhances the welfare and profitability of the non-government sector.
Second, governments directly employ workers to provide a range of services to the public.
Third, the government provides a plethora of transfer payments to the non-government sector in the form of pension and welfare entitlements and other transfer payments. The existence of these transfers means that total government spending exceeds total government purchases of goods and services and wage payments from the non-government sector.
In Chapter 5, we learned that the National Accounts framework did not include transfers as a component of government spending because they do not constitute a final demand for goods and services by government. They are classified as a deduction from total taxes – a netting out effect.
In our models, which are stylisations of the national accounting measures, the flow T (total taxes) indicates net taxes, meaning total tax revenue minus total transfers to the non-government sector.
Table 8.2 shows the proprtion of government spending in total GDP.
[NOTE – a brief descriptive section follows]
[NOTE: TABLE HERE WILL SHOW THE RATIO OF GOVERNMENT SPENDING TO TOTAL NATIONAL INCOME – WE ARE STILL TO DECIDE WHETHER TO CREATE ONE TABLE SHOWING ALL THE COMPONENTS OF THE NATIONAL ACCOUNTS FOR ONE YEAR RATHER THAN SEPARATE TABLES FOR EACH COMPONENT ACROSS A NUMBER OF YEARS AS IN TABLE 8.1]
In Chapter 13, we will learn that government spending overall is determined by two broad forces. First, the policy decisions that the government takes in setting its fiscal policy. Second, the state of the overall business cycle. For example, when the economy is performing badly, government spending will increase as a result of welfare payments even without any explicit change in government policy. The opposite will be the case when the economy is growing strongly and unemployment is falling.
We call these effects cyclical because they vary with the state of the economic cycle. We will consider them in more detail in Chapter 13 when we analyse budgets.
For the purposes of the following discussion, we will assume away these cyclical effects on government spending (G) and assume that it is given by the policy choices of the government and thus is exogenous to national income. We learned about the meaning of exogenous variables in Chapter 4.
Introducing Net Exports
In Chapter 15 we will consider the determinants of net exports in detail when we introduce the exchange rate and measures of international competitiveness.
Exports are goods and services produced in the local economy which are then sold to the rest of the world. The National Accounts includes them in the measure of national production and income because they are produced locally. Export spending is thus an injection of expenditure into the economy from abroad and increases national output and income.
While export spending boosts national income, we consider exports to be a cost in the sense that they deprive the local population of the use of the real resources that are used up in the production of the goods and services sold abroad.
Imports comprise expenditure on goods and services by households, firms and government which are produced by the rest of the world. In other words, some of the consumption expenditure, investment expenditure and government expenditure in each period does not increase local production and is thus considered to be “lost” or “leaked out” of the local expenditure-income loop.
The National Accounts framework thus deducts imports from the estimates of national production and income to recognise that some spending provides demand for goods and services produced by the rest of the world.
By separating the consumption, investment and government spending that leaks out of the economy via imports into a separate category we can clearly appreciate the net effect of external trade. We thus know that the National Account measures of consumption spending (C), private capital formation (I) and government spending (G) include only expenditure on locally-produced goods and services.
Even though import expenditure is a leakage from the expenditure system, we consider them to provide benefits to the local economy by allowing households, firms and government to enjoy access to goods and services not otherwise available or available on competitive (qualitative and/or price) terms.
The difference between exports (X) and imports (M) is called the net exports (NX) of a nation. A trade surplus would occur when exports are greater than imports. A trade deficit occurs when the opposite is the case. We will consider these issues in more detail in Chapter 15.
In this chapter we simplify the model by assuming that exports (X) are given in any year and determined by national income in the rest of the world, which are beyond the influence of the local economy in question.
What determines import spending?
We assume that import spending (M) rises with national income. The higher is the national income, the greater will be the flow of consumer imports and the imports of capital equipment.
We will consider the impact of exchange rate changes on import volumes and values in Chapter 15. For now we assume that a nation imports a fixed proportion of every dollar of national income.
That proportion is called the marginal propensity to import (m) and has a meaning similar to the MPC. The marginal propensity to import is the extra import spending that occurs as a result of a dollar increase in national income.
Our simplified import expenditure model is given as:
(8.10) M = mY
For example, if m = 0.2, then if national income (Y) rises by $100, import spending will increase by $20. The higher is the marginal propensity to import, the higher is the leakage in import spending at every national income level.
Total aggregate expenditure
Now we have considered all the components of aggregate expenditure (or demand) we can write the equation for aggregate demand (E) as:
(8.11) E = C + I + G + (X – M)
This is an accounting statement, which is derived from the National Accounting framework.
However, we have already developed some simple behavioural theories about the individual components of total expenditure. We assumed that consumption and imports were positive functions of national income and that investment, exports and government spending were fixed in each period by factors invariant to national income. We also adopted a simple tax rule.
We can expand the aggregate demand equation to reflect those behaviorual assumptions, which, in turn, will allow us to derive an expression for equilibrium income.
(8.12) E = C0 + c(1 – t)Y + I + G + X – mY
You can see that some components of total expenditure in the economy are dependent on national income levels and some (I, G and X) are, by assumption, independent or autonomous to national income.
We can use the techniques you learned in Chapter 4 to modify Equation (8.12).
(8.13) E = C0 + I + G + X + [c(1 – t) – m]Y
We could usefully simplify this expression by collection all the components of total expenditure that are autonomous (such that A = C0 + I + G + X) to write the Aggregate Demand Function as:
(8.14) E = A + [c(1 – t) – m]Y
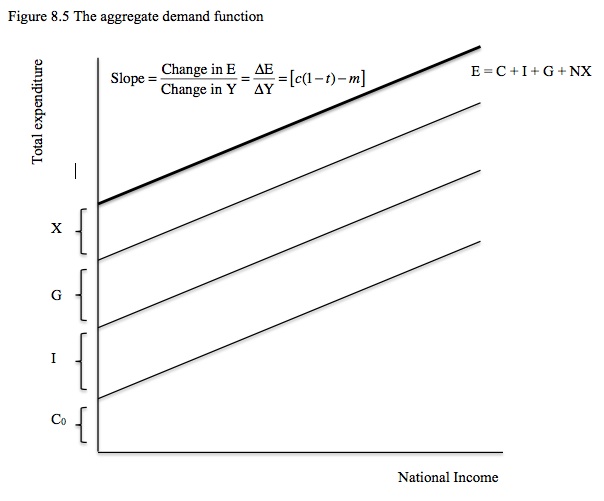
The slope of this function – ΔE/ΔY = [c(1 – t) – m] – which tells us that the change in aggregate spending for a given change in national income is larger, the larger is the marginal propensity to consume (c) and the lower is the tax rate (t) and the marginal propensity to import (m).
See if you can explain this result to yourself at this point. Think about the marginal propensity to consume as leading to an induced consumption expenditure increase when national income rises and the tax rate and marginal propensity to import being leakages from the expenditure system for each dollar rise in national income. We will provide a full analysis of this in the next section when we consider the expenditure multiplier.
Figure 8.5 shows the Aggregate Demand Function and its individual components. We add all the autonomous expenditure items to get the intercept of the function.
[NOTE: equilibrium income to be defined and solved}
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
That is enough for today!
(c) Copyright 2012 Bill Mitchell. All Rights Reserved.
I wonder if you might be kind enough to answer my following question. Do you consider in your theories the change in credit levels in the economy in your formulas or is that for you a negligent aspect?
“The latter category of spending generates the valuable public infrastucture that enhances the welfare and profitability of the non-government sector.”
That sounds odd. I would suggest something along the lines “that increases or maintains efficiency, quality and coverage of public services”. A note that these are both an input in the utility function of households and an important input in the production of private sector firms would be an advantage, too. Human capital and economic growth are the main story, after all. Perhaps a small box on “Education and economic growth” and one on “Public invention turned to private innovation – the source of Apple’s success” would illustrate these points?
In Figure 8.5, the lowest bracket should be C, not C0. C0 might be marked, too, but it is constant (autonomous) whereas in the graph that portion is rising with income.