It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
Sectoral balances – Part 2
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text by the end of this year. Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.
Please refresh your memory of last week’s blog – Sectoral balances – Part 1 – as this section of Chapter 6 builds directly on it.
The Flow of Funds Matrix
The T-accounts tracing the sectoral sources and uses of funds can be summarised for all sectors in the economy by the Flow-of-Funds Transactions Matrix, a stylised version of which is shown in Figure 6.4.
The overriding accounting rule that governs the presentation of the Flow-of-Funds Accounts is that for the economy as a whole and for each sector in the economy the total sources of funds must be equal to the total uses of funds. Remember that sources of funds provided by the various sectors in the economy are used by those sectors.
Figure 6.4 (taken from Ritter, 1963) shows three sectors and the total economy. At the most aggregate level, the three sectors could be the private domestic sector, the government sector and the external sector.
Figure 6.4 A stylised three-sector Flow-of-Funds Matrix
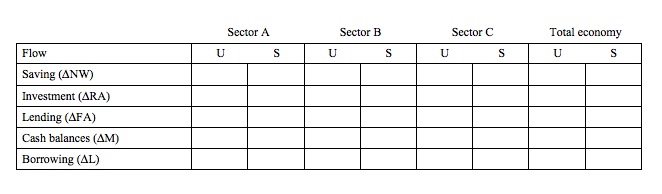
For each period being accounted for, the statistician would record the flows on funds that related to each of the row categories in the matrix. Most importantly, we have learned that for every deficit sector, which saves less than it invests, there has to be offsetting surpluses in at least one other sector.
Lawrence S. Ritter (1963) called the Economy-wide Flow-of-Funds Matrix
… an interlocking self-contained system … [which] … shows, for a specified time period, the balanced sources-and-uses-of-funds statements for each sector, the interrelations among the sectors, and the aggregate totals of saving, investment, lending, hoarding, and borrowing for the economy as a whole. Any one sector may invest more or less than it saves, or borrow more or less than it lends. However, for the economy as a whole, saving must necessarily equal investment, and borrowing must equal lending plus hoarding.
Thus a deficit sector, which saves less than it invests, must be offset by at lease one other surplus sector to net the flows to zero.
What are the practical uses of presenting economic data in this way?
Various uses can be made of the information provided in the Flow-of-Funds Accounts.
The Flow-of-Funds Accounts provide information of all financial flows within the economy on a sector-by-sector basis. They allow researchers and policy makers to understand how funds flow from one sector (say the household sector) through the banking system and onto final uses by, for example, forms engaged in productive investment.
They also allow researchers and policy makers to monitor major economic trends such as the changing indebtedness of the sectors included and the sources of funding for the respective sectors. For example, an understanding of the Flow-of-Funds Accounts would have provided insights into the growing indebtedness of the private sector prior the Global Financial Crisis and perhaps, alerted policy makers to the unsustainability of these trends.
Economic researchers also use the Flow-of-Funds accounts to study saving patterns in the economy. The Accounts can tell us where the saving of a sector are being deployed – which financial and real assets. They also allow us to understand patterns of gross capital formation.
Economic researchers also use the Flow-of-Funds accounts to examine the dynamics of such concepts as household wealth. We can learn how household balances sheets change over time and how that wealth is composed. For example, one of the hallmarks of the period leading up to the Global Financial Crisis in many countries was the shift in household wealth to riskier categories, such as share holdings sourced from margin loans. The shift in importance in overall wealth from the more secure homemortgages to more riskier sources of wealth was significant because it exposed the economies to an increased risk of financial instability.
Finally, central banks use the Flow-of-Funds accounts to help them estimate the sensitivity of the economy to changes in the availability of credit.
Flows of Funds in reality
Every 3 months (March, June, September and December), the US Federal Reserve Bank publishes the – Flow of Funds Accounts of the United States. The latest issue (at the time of writing was published on – September 20, 2012.
While the official data presentation is much more complex than our simplified matrix, the Flow-of-Funds accounts presented by the US Federal Reserve remain faithful to the conceptual structure set out in this Chapter.
[SECTION HERE ON ANALYSING AN ACTUAL TABLE – MAPPING THE CONCEPTUAL CATEGORIES IN TO THOSE USED BY THE FEDERAL RESERVE – ESPECIALLY IN THE BALANCE SHEET AND FLOW TABLES THEY PRODUCE]
Further reading:
You might like to read this research paper from the US Federal Reserve Bank – Teplin, A.M. and Tyler, A.M. (2001) ‘The U.S. Flow of Funds Accounts and Their Uses’, Federal Reserve Bulletin, July, 431-441 – DOWNLOAD.
Flow-of-Funds Accounts and the National Accounts
The Flow-of-Funds Accounts complement the National Accounts and the Balance of Payments Accounts, which are produced by national statistical agencies on a regular basis as a way of measuring economic activity in total and across the broad economic sectors.
We will consider the Balance of Payments Accounts in Chapter 15.
There are important differences between the Flow-of-Funds accounts and the National Accounts, which can be summarised as:
- The National Accounts contain no data pertaining to financial transactions – borrowing, lending or changes in cash balances. Only non-financial transactions are measured. The Flow-of-Funds accounts fill that void.
- The National Accounts focus on the current flows of final expenditure, output and income. As we saw in Chapter 5, transactions that involve so-called double counting are eliminate intermediate transactions. The Flow-of-Funds accounts allow us to trace transactions involving assets that have been created in past periods.
- The structure of the National Accounts is such that consumer durable expenditure is included under current expenditure when conceptually it should be considered investment activity. In the Flow-of-Funds accounts all sectors can invest and save.
The Sectoral Balances view of the National Accounts
The flow-of-funds framework allows us to understand that the funds a particular sector receives during a period from current receipts, borrowing, selling financial assets, and running down cash balances have to be equal to the total of its current expenditures, capital expenditures, debt repayments, lending, and accumulation of cash balances.
The flow-of-funds matrix clearly allows us to trace the uses and sources of funds for each sector.
A related approach, which also brings the uses and sources of national income together, is the sectoral balances perspective of the national accounts.
The most basic macroeconomics rule is that one person’s spending is another person’s income. At the sectoral level the same proposition holds. Another way of stating this rule is that the use of income by one person will become the source of income for another person or persons. Similarly, at the sectoral level.
In Chapter 5, we saw that the National Accounts divided the national economy into different expenditure categories – consumption by persons/households; investment by private business firms; spending by the government; exports to and imports from the foreign sector.
We can view that division in two ways:
1. From the perspective of the sources of total spending. So consumption (C), investment (I), government spending (G), exports (X) minus imports (M). In Chapters 7 and 8 we will develop theoretical models of each of these components. But for now we simply take them as given and understand them to be parts of the defined national accounts of a nation.
The various types of spending when summed equal aggregate demand. Aggregate demand, in turn, generates a response by producers (private and public) in the form of production, which, in turn, generates flows of income to suppliers of inputs into production (wages, profits). The sum of those flows equals national income.
2. The second perspective thus focuses on the uses of the income produced in response to the spending sources. At the aggregate level, national income can be used to consume, save or pay taxes.
[NOTE HERE ABOUT THE DISTRIBUTION OF NATIONAL INCOME DOWN TO THE INDIVIDUAL – SO “COMPANIES”, ULTIMATELY, DON’T EXIST]
We can express these two perspectives in shorthand in this way. From the perspective of the sources of national income we can write out the expenditure side of the national accounts as:
(6.1) GDP = C + I + G + (X – M)
that is, total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
Total national income (GDP) can be used for:
(6.2) GDP = C + S + T
which says that GDP ultimately comes back to households (after all the distributions are made) who use it to fund consumption (C), saving (S) or to pay taxes owing to the government (T).
You will see that these two perspectives are of the same outcome – national income. Remember the flow of spending (source) has to equal the flow of income in each period (which is used in some way).
To show this we write:
(6.3) C + I + G + (X – M) = GDP = C + S + T
If we simplify this – remembering the tools we developed in Chapter 4 Methods, Tools and Techniques – by cancelling out common terms on both sides of the equation (in this case, C) and re-arranging the terms within the rules that govern equations (what you do to one side of the equals sign you have to do to the other side), we can express the sources and uses of income flows on a sector by sector basis.
We saw this was possible when we constructed the Flow-of-Funds matrix earlier in the Chapter.
Thus:
(6.3a) I + G + (X – M) = S + T
The three sectors captured by the national accounts at this level of aggregation are the government sector (G, T), the private domestic sector (S, I) and the external sector (X, M). We can collect the individual terms in Equation (6.3) for the three sectors in a number of ways, depending what interpretation we wish to derive.
Here is the first way of re-arranging Equation (6.3a):
(6.4) (I – S) + (G – T) + (X – M) = 0
Each of the terms on the left-hand side of the equals sign represent the balance between spending (sources) and income (uses) for each sector. The net result of the two flows is the balance flowing in that sector over the period that the national accounts are expressed for.
Equation (6.4) is therefore called the sectoral balances view of the national accounts.
The sectoral balances derived are:
- The private domestic balance (I – S) is positive (deficit) if the private domestic sector is spending more than it is earning; and negative (surplus) if the sector is spending less than it is earning overall.
- The Budget Deficit (G – T) is positive (deficit) if the government is spending more than it is taking out of the economy in taxation; and negative (surplus) if the government is not adding as much spending to offset the taxes it is taken out of the economy.
- The External balance (X – M) is positive (surplus) if the nation is generating export income in excess of the spending that is lost to the domestic economy through import spending; and negative (deficit) if the import spending is larger than the flow of income coming in through exports.
This way of expressing the sectoral balances makes it easy to understand that the sum of the balances for each sector must necessarily sum to zero. The sources of income must be exactly equal to the uses. That doesn’t mean that each sector has to be in balance at all times and in the real world that is almost never the case.
What it means that the surpluses and deficits have to cancel out when we consider the economy as a whole.
Another way of re-arranging Equation (6.3a) is as follows:
(6.5) (G – T) = (S – I) – (X – M)
The same conclusion applies – the left hand side balance (the Budget Balance) has to equal the sum of the two right hand balances. Note the private sector balance is written differently this time as a result of the way we re-arranged the terms. But it still depicts the balance between spending and income for that sector overall. It just means that a positive balance will be a surplus (spending less than income) and vice versa.
This representation of the sectoral balances allows us to highlight another feature of the macroeconomy. The two balances on the right-hand side represent the non-government sector – the sum of the private domestic sector and the external sector.
Thus Equation (6.5) can be interpreted as saying, that at all times:
- A government deficit (G > T) has to equal to a non-government sector surplus – (S – I) – (X – M) < 0, and
- A government surplus (G < T) has to equal to a non-government sector deficit - (S - I) - (X - M) > 0.
These are accounting statements. In Chapters 7 and 8, we will develop theories and conceptual understandings that allow us to explain the underlying macroeconomic processes that are involved that render the individual balances consistent with the accounting.
Note in policy discussions, the balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
How can we use the sectoral balances framework?
Figure 6.5 shows the quarterly movement in the sectoral balances for the US from the March-quarter 1955 to the December-quarter 2011 for the Private domestic sector (S – I) and the Government sector (G – T).
The movements in the Private Domestic Balance and the Government Budget Balance are closely aligned until the early 1980s. Thus, we can see that when the Private domestic sector is in surplus overall there is an almost equal government deficit and when the private sector moves into deficit overall, the government budget moves in to surplus.
After the 1980s, the two balances diverged in magnitude although they still moved in sympathy with each other – that is, the direction of movement and the turning points remain closely aligned across time.
The movements in Figure 6.5 cannot tell us about causality – that is, which balance might be driving the other. We need to add theory and an evidence base to our analysis before we can make definitive statements about the direction of causality. In some cases, historical and contextual study will reveal that the changes in the government balance (driven by discretionary changes in government fiscal policy) have led to changes in the private domestic balance. At other times, the causality will be in reverse. And in some periods, the causality will be bi-directional – that is, the behaviour of both sectors is influential for the outcomes revealed by both.
Figure 6.5 Sectoral Balances, Private Domestic and Government Sectors, United States, 1955Q1 to 2011Q4
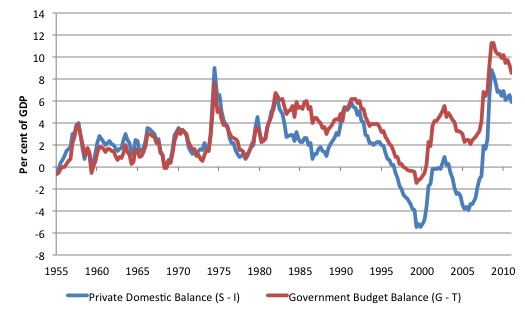
Source: DOCUMENT SOURCE
Why do you think the gap between the two balances widened since the 1980s? The answer to the question is revealed by studying Figure 6.6, which adds the external balance (X – M) to the graph.
Up until the 1980s, the external balance was close to zero, which meant that exports minus imports (adjusting for net income transfers) were balanced. After the 1980s, the US economy began to import more than it exported and the external balance moved into deficit. The increasing (and variable) gap between the private domestic balance and the government balance since that time reflects the growing (and variable) external balance.
In Chapter 18 Policy Debates we will consider some of the competing views among economists of these movements.
Figure 6.6 Sectoral Balances, Private Domestic, Government and External Sectors, United States, 1955Q1 to 2011Q4
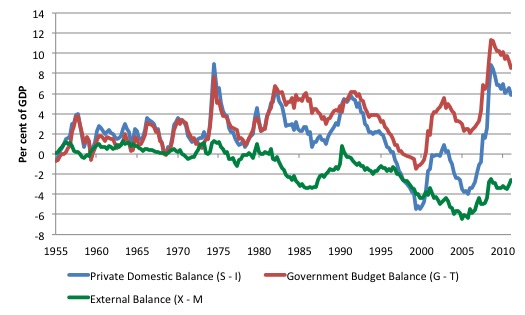
Source: DOCUMENT SOURCE
A simple application
As a reaction to the Global Financial Crisis, many governments have begun to impose fiscal austerity on their economies in the mistaken belief that rising budget deficits represent the source of the crisis. We will consider the GFC and its aftermath from the perspective of policy choices in Chapter 18 Policy Debates.
But for now we can express the desire for austerity in terms of the government introducing discretionary spending cuts and/or tax rate increases aimed at reducing the size of the government balance (G – T).
For example, the National Accounts data provided by the US Bureau of Economic Analysis allows us to calculate the sectoral balances for the US economy. In the fourth-quarter 2011, for example, the private domestic sector balance was in surplus of 5.9 per cent of GDP. The External Balance was in deficit of 2.7 per cent of GDP and the Government Budget Balance was in deficit of 8.6 per cent of GDP (these numbers are rounded up).
You can see that they satisfy Equation (6.5), (G – T) = (S – I) – (X – M):
(G – T) = (S – I) – (X – M)
8.6 = 5.9 – (-2.7)
If we round these balances into whole numbers to make it a little easier to work with we might assume that the budget deficit is 8 per cent of GDP, the private domestic balance is 6 per cent of GDP and the external deficit is 2 per cent of GDP.
Now imagine the government desires to reduce its budget deficit to 2 per cent of GDP in the coming year and embarks on a stringent campaign to cut government spending.
If it achieved that aim and the external deficit was, for argument sake, unchanged, then the private domestic sector surplus would disappear. The reason, which will be explained in detail in Chapters 7 and 9, is that the large cuts in government spending (a source of national income) would lead to large reductions in real GDP and national income, which in, turn would cut disposable income and reduce the capacity of the private domestic sector to save.
We will learn that the situation would be more complicated than that in the real world because the reduction in economic activity brought about by the fiscal austerity would also reduce government tax revenue and imports. Further, the lower consumer spending associated with the fall in disposable income would also likely feed into reductions in private investment.
It is thus difficult to isolate one component in a sectoral balance and assume it will impact in a predictable way on another component in another balance. We will learn in Chapters 7 and 8, that individual balances are all connected causally via changes in national income and to make predictions about the way in which the balances will move and resolve we need to have theories about what generates these national income changes.
But from an accounting perspective if the external balance is zero, then the private domestic balance will be the exact opposite in sign and equal in magnitude to the budget balance. We can tell many narratives about different combinations of these balances.
A graphical framework for understanding the sectoral balances
[NOTE THIS SECTION WILL DEVELOP AND UTILISE THE THREE SECTOR GRAPHICAL FRAMEWORK SUMMARISED BY THE FOLLOWING FIGURE – WILL BE IMPROVED UPON VISUALLY NEXT WEEK]
Figure 6.7 A Graphical Sectoral Balances Framework
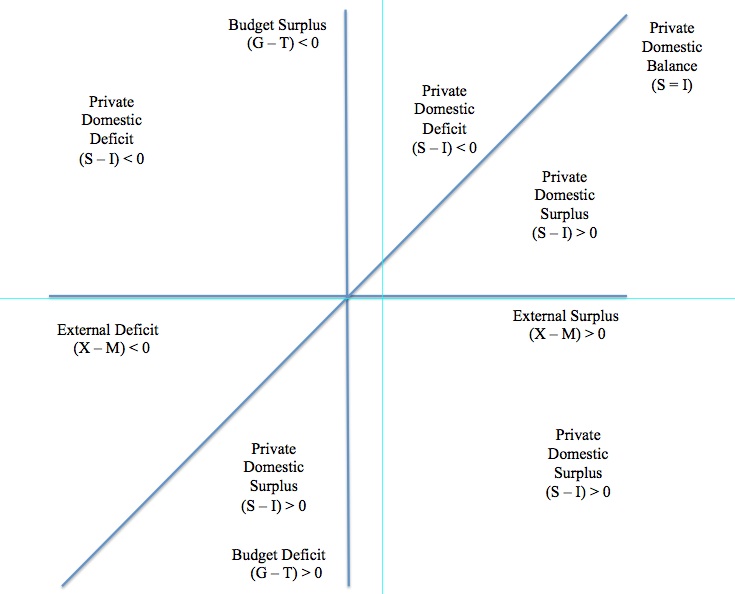
Source: DOCUMENT SOURCE
[NOTE: THE FOLLOWING SECTION IS CONSIDERED ADVANCED MATERIAL WHICH WILL BE IN THE INTERMEDIATE SEQUENCE THAT WILL BE DEFINED IN THE TEXTBOOK. ALTHOUGH IF SYMPATHETICALLY TAUGHT IT CAN BE EXPLAINED TO INTRODUCTORY STUDENTS]
The flow of funds and modern monetary macroeconomics
In the last section, we built a simple accounting framework for tracing the flow-of-funds within the economy which provided an additional perspective to the way in which the National Accounting framework presents the relationships between the main spending aggregates.
The A Flow-of-funds approach to the analysis of monetary transactions provided a basis for understanding the relationship between the flows of expenditure by the different sectors and how they could impact on measured stocks of financial and real wealth in the economy held by these sectors.
In Chapter 3 Government and Money, we distinguished between vertical transactions between the government sector and the non-government sector and horizontal transactions within the non-government sector.
In this section, we demonstrate how a flow-of-funds approach to the analysis of monetary transactions highlights both the importance of the distinction between and vertical and horizontal transactions and the fundamental accounting nature of the so-called government budget constraint (GBC) identity.
This section will provide you with the categorical understanding that that the GBC is an ex post accounting identity rather than an ex ante financial constraint. That means that while the GBC is true by accounting definitions and will hold if we measure the components at any point in time, it has no meaning if we want to think of it as a constraining financial rule that governments must adhere to when they are planning expenditure.
When they do spend, the GBC will “add up” consistently but that is a fairly unimportant insight.
What the flow-of-funds approach can also demonstrate is the proposition that if the sovereign government runs cumulative budget surpluses which destroy net financial assets held by the non-government sector, then the latter must accumulate equal deficits in the form of increasing indebtedness. While the concept of sustainability has little meaning in the case of a government deficit – that is, there is no question that the government can run whatever deficit is required, given the state of overall spending in the economy, continuous non-government deficits are unsustainable because the capacity to pay the increasing levels of debt is, at some point, exhausted.
That is a fundamental difference between the currency-issuer (government sector) and the currency-user (non-government sector), which underpins many interesting insights in modern macroeconomics.
The flow-of-funds framework developed in the last section leads logically to what is termed as the current transactions matrix, which is depicted in Figure X.X.
The columns denote the sectors that we are dividing the economy up into. We could construct the matrix just for government and non-government, but this would negate an depiction of the horizontal relationships between various sub-sectors of the non-government sector (for example, households, firms, banks).
The rows of the matrix depict flows of expenditure (consumption, investment, government) and incomes derived from the supply of inputs to the production process (wages, taxes, interest, dividends)
[MORE TO COME ON THIS TOPIC SOON]
Conclusion
NEXT WEEK I PLAN TO TIDY THIS CHAPTER UP AND MOVE ON TO CHAPTER 10 WHICH CONSIDERS INTRODUCTORY ISSUE PERTAINING TO LABOUR MARKETS – CONCEPTS, MEASUREMENT, ETC.
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
That is enough for today!
(c) Copyright 2012 Bill Mitchell. All Rights Reserved.
Dear Bill,
I was wondering about the use you make of the “national accounts” term by which I think you mostly refer to the various measurements of GDP and GNP to which, in your usage of the terms, the flow of funds and balance of payment reports/accounts are complements.
Perhaps you should somewhere give a more aggregate view of the System of National Accounts or SNA which encompasses the GDP, BOP and flow of funds accounts (the latest manual, I believe, is here: http://unstats.un.org/unsd/nationalaccount/docs/SNA2008.pdf). This manual reports the internationally agreed methodology for measuring the national accounts and there is a lot of interesting discussion on sectoral balances. I mean, that is if you make a clever use of the “find” function in your pdf reader and manage to survive a pretty dry 722 page document.
In the SNA there are a lot of complicated intermediate accounts which in my experience nobody uses in analysis, but there is a very good comprehensive view on how everything fits together and the challenges of time of recording, price and valuation adjustments, etc. and how you have to take everything with quite a pinch of salt.
The concept of the ROW is something that I admit I struggle with in the context of the other accounts, and it could be great if you dedicate some time to discussing the relationship between the ROW stocks and flows, the IIP (stock), the BOP (flows) and the external debt reports (which are not part of the SNA).
Regards,
Javier
“You can see that they satisfy Equation (6.5) – (G – T) = (S – I) – (X – M):”
This makes it look like you are trying to say “-(G-T) = (S-I)-(X-M)”. I.e. it looks like you’re trying to say “minus, bracket, government spending minus taxation”.
Also, the example doesn’t quite add up. You end up with:
8.6 = 5.9 – (-2.6)
Which is:
8.6 = 8.5
I’m sure its just an accounting mistake, but you should probably explain it.
Dear Philip Pilkington (at 2012/10/20 at 7:40)\
Thanks for your comments.
I have put a comma in rather than a hyphen to avoid that misinterpretation.
In terms of adding up, I had in the previous paragraph said the numbers were rounded, which in normal parlance will warn you that strict adding up will probably not work out.
To avoid that issue, I have just rounded up a bit more.
best wishes
bill
(I – S) + (G – T) + (X – M) = 0
What is the stock that flows here?
What if that equation is incomplete?
Dear Bill
Here is some one trying to understand MMT from China…well,I have look at the Flow of Funds Accounts of the United States from FED, The all sector uses is not equal to all sector sources, which makes me confused…Can some one explain this?
Best Regards