It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
External economy considerations – Part 3
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text by the end of this year. Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.
[This continues the discussion from rough draft of last week – External economy considerations – Part 2. At some point the pedagogy will be assessed and edited into a final draft]
15.5 Trade in goods and services, product market equilibrium and the trade balance
15.5.1 National income equilibrium with trade
In this Section, we continue to assume that Pw/P is constant, which means that domestic and foreign firms respond to increases in real aggregate demand by increasing real output rather than prices.
Spending on domestic goods determines real output and income. Total spending on domestically produced goods and services is equal to total spending by domestic residents minus their spending on imports plus foreign demand for exports.
Referring back to Chapter 8 and Chapter 12 we have the following behavioural equations, which comprise our theory of aggregate demand:
(15.5) Consumption function C = C0 + cYd = C0 + c(1 – t)Y
(15.6) Investment function I = I0 – bi
(15.7) Government spending G
(15.8) Net exports NX = λYw – mY + θe
Note that we have &theta is the net impact of changes in the real exchange rate, here expressed as the nominal exchange rate because we assume that Pw/P is constant.
We can substitute the individual behavioural equations into the equilibrium income Equation (15.2) such that:
(15.9) Y = E = C0 + c(1 – t)Y + I0 – bi + G + λYw – mY + θe
Which, if we refer back to the way we simplified the equations to finally get Equation (8.16), we can write:
(15.10) Y = 1/[1 – c(1 – t) + m] times [C0 + I0 – bi + G + λYw + θe]
This expression for equilibrium national income tells us that real GDP (Y) will be the sum of all the expenditure terms that do not directly depend on national income (those in the right-hand bracketed expression) times the multiplier (the first left-hand side term).
[NEW MATERIAL FOR THIS WEEK STARTS HERE]
15.5.2 The Net Exports function
Equation (15.8) represented net exports (NX) in terms of world income (Yw), domestic national income (Y) and the exchange rate (e). The latter term was the net impact on aggregate spending of an exchange rate change taking into account the different impacts on the individual components, exports and imports.
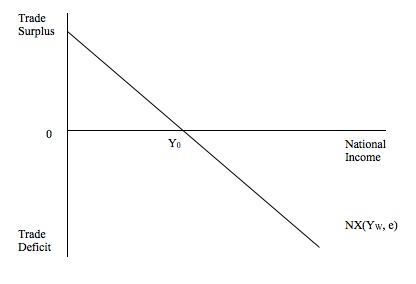
Figure 15.3 show the Net Exports function in terms of national income. Above the zero point on the vertical axis economy would be in trade surplus and below the zero point a trade deficit.
The Net Exports function is drawn against national income with the other variables in Equation (15.8), Yw and e, being held constant. If either of these variables changed the NX function would move up or down, depending on which of the variables changed and our assumptions about the parameters λ (for a change in world income) and θ (for a change in the nominal exchange rate).
We have assumed that λ > 0 so that an increase in world income levels boosts our exports and so net exports rises (other things equal). Further, in our discussion we assumed that the net impact on net exports of a change in the exchange rate, which is measured by θ is positive. This means that an exchange rate depreciation improves the trade balance.
In other words we conclude that:
- If world income rises (falls) the Net Exports function will move out (in) with unchanged slope.
- If the exchange rate depreciates (appreciates) the the Net Exports function will move out (in) with unchanged slope.
If we assume both the shift variables (Yw and e) are constant, then as national income rises the trade balance will be negatively sloped – that is, move from a surplus to a deficit.
This is because as national income rises, imports rise via the marginal propensity to import (m). At point Y0, the net exports are balanced (exports equals imports).
To summarise, to the left of NX = 0, there is a trade surplus because, for a given level of exports, the lower level of income leads to a smaller expenditure on imports. To the right of NX = 0, there is a trade deficit, because at the higher level of income, imports are higher, relative to the fixed level of exports.
The slope of the Net Exports function is determined by the marginal propensity to import. The larger is the marginal propensity to import the steeper the slope. This is because the larger is the marginal propensity to import the greater the leakage from the expenditure stream per extra dollar of national income generated and the more quickly the trade balance moves into deficit at each income level.
Figure 15.3 Net exports as a function of real national income
We an use this understanding and that provided by the equilibrium national income expression (Equation 15.10) to study what happens to national income when world income and/or the exchange rate changes.
15.5.3 The impact on national income and net exports of a change in world income
We have seen (from Equation 15.10) that the equilibrium level of national income (and real GDP) is dependent on the level of domestic autonomous expenditure (C0 + I0 + G; the interest-rate sensitive component of investment (bi); the level of world income (Yw) and the real exchange rate (simplified to e because relative prices are fixed).
What happens to national income if either the level of world income or the exchange rate changes? In the analysis that follows we assume that the central bank supplies the monetary base at a constant discount rate, so that the interest rate charged by the commercial banks can be treated as constant.
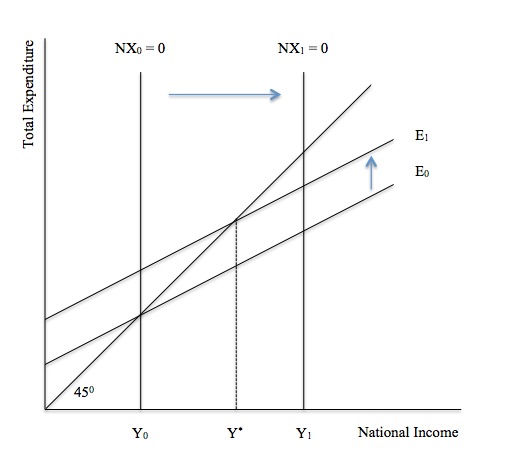
Figure 15. 4 reintroduces the Aggregate Demand function from Chapter 8. Recall Figure 8.6 which showed that a rise in autonomous spending would lead to the Aggregate Demand function shifting up in parallel fashion (the shift in the intercept being measured by the change in autonomous spending). It is straightforward to generalise that insight into the current context by noting that the autonomous expenditure components are just the right hand terms in Equation !5.8 which interact with the spending multiplier.
In Figure 15.3 the trade balance line is denoted as NX = 0. With the other determinants constant (world income and the exchange rate), we noted that there was one level of national income where the trade account would be balanced (where imports equal exports). We denoted that level of national income as Y0 in Figure 15.3.
We can translate that knowledge into Figure 15.4 by drawing an NX0 = 0 line which corresponds to national income level Y0. All national income levels below Y0 will result in trade surpluses because imports will be lower than exports, other things equal. All national income levels above Y0 will generate trade deficits, because imports will be higher than exports, other things equal.
In our discussion of Figure 15.3, we also noted that the NX line would shift up if world income increased and down if world income decreased. In the context of Figure 15. 4, this means that the NX = 0 line will shift to the right if world income rises and to the left if world income falls.
The reason is simple. Start from national income level Y0, which initially coincides with a trade balance NX0 = 0. If world income rises, then at that national income level (Y0), exports will be higher than before and so the trade account would be surplus. Trade balance would require a boost to imports, which, in turn, would occur at higher levels of national income. We denote the new trade balance NX1 = 0 at Y1.
But we also know that a rise in world income will lead to the rest of the world importing more goods and services from the domestic economy which means exports rise. As we learned in Chapter 8, if any of the expenditure components rise, then the Aggregate Demand function shifts upwards.
Figure 15.3 denotes an initial point Y0, which just by coincidence is also a point of external balance. Aggregate demand is at E0.
The rise in exports pushes the Aggregate Demand function upwards to E1 and the new national income equilibrium occurs at Y*. At this point, real GDP is higher, national income is higher and we could show that employment would be higher and unemployment lower, once the cyclical labour supply adjustments that we studied in Chapter 10 were exhausted.
You will also note that the economy now has an external surplus, being left of the NX1 = 0 line (see Advanced Material for an explanation).
Figure 15.4 Equilibrium national income with a change in world income
By way of summary, a rise in world income induces a rise in foreign purchases of the economy’s exports, in the same way that the local economy’s import demand will be stimulated if its national income rises.
This has two effects:
- The Aggregate Demand line (E0) shifts upwards by the initial injection of aggregate demand from exports (ΔX), giving rise to a new level of equilibrium national income Y*. The increase in equilibrium national income is given by 1/[1 – c(1 – t) + m] times ΔX, given the constant interest rate. This is just a specific example of the general result that the aggregate demand schedule shifts in response to changes in autonomous spending;
- The NX = 0 line shifts to the right from NX0 = 0 to NX1 = 0.
- Imports rise too because the shift in the Aggregate Demand line (to E1) means that income levels are higher. But the shift in the NX = 0 line is greater than the increase in equilibrium income. Thus NX rise, but by less than the rise in exports. This result holds even if domestic interest rates rise.
|
Advanced Material – An increase in World Income leads to a rise in Net Exports
Prior to the rise in world income, the level of real GDP, Y0 is consistent with a balance of trade, NX0 = 0. Assuming no change in the exchange rate, we can write this as: (15.11) X0 = M0 + mY0 where the M0 is a constant quantity of imports at the current constant exchange rate. If we denote ΔX = λΔYw, which is the increase in exports resulting from the rise in world income, then national income Y1 at which net exports are zero, satisfies: (15.12) X0 + ΔX = M0 + mY1 If we subtract Equation (15.11) from (15.12) we get: (15.13) ΔX = mY1 – mY0 = mΔY‘ So the change in the level of real GDP, such that net exports are again zero is given by: (15.14) ΔY‘ = ΔX/m On the other hand, the increase in equilibrium real GDP (national income) resulting from an autonomous increase in exports (driven by the rise in world income) is given by (from Equation 15.10): (15.154) ΔY = 1/[1 – c(1 – t) + m] times ΔX This magnitude is less than ΔX/m because [1 – c(1 – t) + m] > 0. Thus at the new national equilibrium, Y*, net exports are positive – that is, in surplus. |
You should be able to work out what would happen if there was a world recession and world income levels fell. In this case, the local economy will experience a drop in aggregate demand because exports will be lower than previously and national income will fall.
The NX = 0 line also shifts to the left and if the economy was, for simplicity, experiencing a trade balance, then the new equilibrium income level will be associated with a trade deficit (the fall in exports is greater than the fall in imports).
MORE COMING.
Conclusion
NEXT WEEK I WILL CONTINUE TO EXPAND THE TEACHING MATERIAL FOR CAPITAL FLOWS AND THE CAPITAL ACCOUNT AND DISCUSS POLICY OPTIONS
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
That is enough for today!
(c) Copyright 2012 Bill Mitchell. All Rights Reserved.
I get the accounting level fine but I am having difficulties understanding the operational side of things at commercial banks and central bank level. Where can I find information about this? If I bring foreign currencies to my local bank to get the national currency, where do my foreign currencies eventually end up in the system? Are they stored at the National Central Bank, thereby building foreign currency reserves? Or are they returned to the foreign central banks in exchange for currency-denominated accounts held by the National Central Bank?