It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
Unemployment and inflation – Part 5
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text during 2013 (to be ready in draft form for second semester teaching). Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.
This is the continuation of the Chapter on unemployment and inflation – the series so far is:
- Unemployment and inflation – Part 1
- Unemployment and inflation – Part 2
- Unemployment and inflation – Part 3
- Unemployment and inflation – Part 4
I am now continuing Section 12.6 on the Phillips Curve …
Chapter 12 – Unemployment and Inflation
MATERIAL HERE NOT REPEATED
To see how the Samuelson and Solow (1960) price inflation Phillips curve can be rationalised, we go back to Chapter 9, where we introduced a model of mark-up pricing where firms price by adding a percentage margin to unit costs, which reflects their desired revenue. This, in turn, is consistent with their desired rate of return on capital.
The simplified price mark-up model we introduced in Chapter 9 was:
(12.1) P = (1 + m)WN/Y
where where P is the price of output, m is the per unit mark-up on unit labour costs, W is the money wage, N is total employment and Y is total output. WN is the total wage bill.
We also learned that N/Y is the inverse of labour productivity (Y/N), which means that we could express the mark-up model as:
(12.2) P = (1 + m)W/LP
If we expressed this in rates of change we would be able to say that the inflation rate will be stable if the mark-up is constant and the growth in money wages is exactly offset by the growth in labour productivity.
In other words, growth in labour productivity provides the economy with non-inflationary room to expand money wages (and real wages). As long as money wages grow in proportion with labour productivity growth, unit labour costs (W/LP) will be constant and our simplified mark-up model would predict that prices would be stable.
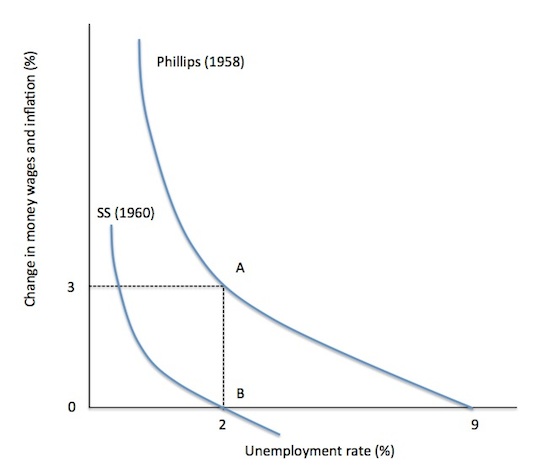
Consider Figure 12.6, which plots two Phillips curve. Note on the vertical axis we are measuring both the rate of change of money wages and the rate of price inflation. In that sense, we are combining the Phillips (1958) curve, which related money wage inflation to the unemployment rate and the modified Phillips curve outlined in Samuelson and Solow (1960), who related price inflation to the unemployment rate.
The curve denoted Phillips (1958) shows that money wage inflation per annum is zero when the unemployment rate is 8 per cent. When the unemployment rate is at 2 per cent, the state of the labour market is such that money wage inflation rises to 3 per cent (per annum).
The SS (1960) curve is the price inflation modified Phillips curve. It cuts the horizontal axis at an unemployment rate of 2 per cent, which means that the rate of price inflation is zero, whereas the rate of money wage inflation is 3 per cent.
The vertical difference between the two curves – measured by the distance AB – is the current rate of productivity growth (which in this case would be 3 per cent per annum).
In other words, in this example, the unemployment rate that is consistent with zero (stable) inflation is 2 per cent.
Figure 12.6 Wage and Price Phillips curves
A more complex and realistic price mark-up model would take into account non-labour costs such as raw material and energy costs (denoted rm). We might define total unit costs to be the sum of labour and non-labour costs per unit of output produced and the resulting mark-up equation would be:
(12.2) P = (1 + m)[W/LP + rm/Y]
This means that with a constant mark-up (m), firms will increase their prices if there is a raw material price shock even if unit labour costs are constant.
We will return to the role of so-called supply shocks (for example, raw material price rises) later when we discuss theories of inflation and the way in which an external price shock can complicate the conflict that workers and capital have over the distribution of national income, which plays out in efforts to defend real wages and mark-ups.
The price inflation Phillips curve was accepted by policy makers in the 1960s and into the 1970s as an integral part of their macroeconomic tools box. By assuming it was stable over the policy setting horizon and would not shift in response to policy changes (that is, they assumed it was not an endogenous relationship), the Phillips curve immediately defined attainable and unattainable combinations of unemployment and inflation.
Consider Figure 12.7 which shows a price inflation Phillips curve (price inflation on the vertical axis). Policy makers considered any point along an estimated Phillips curve to be feasible given the dynamics of the labour market. So it could choose to target a lower unemployment rate, for example, Point A, knowing that in relation to say, Point B the policy choice would lead to higher inflation than before.
From any particular point on the curve, the slope of the curve (denoted here at Point A by the red line) would tell the government how much inflation they would have to bear for a given reduction in the unemployment rate. The slope of the Phillips curve is thus the magnitude of the trade-off between inflation and unemployment.
Another way of thinking about this is that the slope told the government the percentage point rise in the unemployment rate for every percentage point reduction in the inflation rate. So they could use the Phillips curve to calculate the real impacts of a contractionary fiscal and/or monetary policy strategy designed to reduce inflation.
Furthermore, it is obvious that any combination of inflation and unemployment “inside” the Phillips curve (the shaded area in Figure 12.7) are unattainable. The trade-off forced on the government by the dynamics of the pricing process and the way that firms responded to rises or falls in excess demand for labour dictated the possible outcomes.
Figure 12.7 The unemployment-inflation choice set

What would be the best choice for government? Ultimately that became a political matter and governments tried to assess what the socially acceptable combination of the twin evils – inflation and unemployment – might be. Depending on the ideological preferences of the voters, some nations might choose Point B on Figure 12.7 while other nations would be more comfortable with Point A and the higher inflation that accompanied the lower unemployment rate at that level of economic activity.
The problem for government that the Phillips trade-off presented is that the combinations of inflation and unemployment that were considered to be socially acceptable might bot have been possible in terms of the available trade-offs. For example, voters might be very averse to both inflation and unemployment and only hold preferences that fell in the shaded area.
[NOTE – RUN OUT OF TIME TODAY – WE ARE HEADING INTO A DISCUSSIONS OF POLICIES THAT MIGHT SHIFT THE PHILLIPS CURVE PRIOR TO ADDING EXPECTATIONS TO IT]
Conclusion
NEXT TIME I WILL FINISH THE ORIGINAL PHILLIPS CURVE AND CONSIDER THE RESPONSES TO IT LEADING UP TO THE EVOLUTION OF THE NATURAL RATE OF UNEMPLOYMENT APPROACH WHICH STILL DOMINATES.
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
That is enough for today!
(c) Copyright 2013 Bill Mitchell. All Rights Reserved.
Typo near the end, bot is used and it should be not.
I look forward to the final book.