Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – March 16, 2013 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
The accumulated stock of government spending associated with continuous budget deficits can increase the risk of inflation faced by an economy.
The answer is False.
This question tests whether you understand that budget deficits are just the outcome of two flows which have a finite lifespan. Flows typically feed into stocks (increase or decrease them) and in the case of deficits, under current institutional arrangements, they increase public debt holdings.
There is no “accumulated stock of spending” associated with budget deficits. The expenditure impacts of deficit exhaust each period and underpin production and income generation and saving. Aggregate saving is also a flow but can add to stocks of financial assets when stored.
Under current institutional arrangements (where governments unnecessarily issue debt to match its net spending $-for-$) the deficits will also lead to a rise in the stock of public debt outstanding. But of-course, the increase in debt is not a consequence of any “financing” imperative for the government. A sovereign government is never revenue constrained because it is the monopoly issuer of the currency.
This is not to say that in each period the deficit may increase the inflation risk – depending on how fast nominal aggregate demand is growing relative to the real capacity of the economy to respond to it.
The following blogs may be of further interest to you:
- Deficit spending 101 – Part 1
- Deficit spending 101 – Part 2
- Deficit spending 101 – Part 3
- Fiscal sustainability 101 – Part 1
- Fiscal sustainability 101 – Part 2
- Fiscal sustainability 101 – Part 3
Question 2:
If a nation was running a current account deficit and a budget surplus equal to 2 per cent of GDP, we would always observe that the private domestic sector was spending more than it is earning.
The answer is True.
We could consider three options relating to this question:
- A: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending less than they are earn.
- B: A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning – this is the proposition entertained by the question.
- C: A nation can run a current account deficit with a government sector surplus that is larger, while the private domestic sector is spending less than they are earning.
This is a question about the sectoral balances – the government budget balance, the external balance and the private domestic balance – that have to always add to zero because they are derived as an accounting identity from the national accounts.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X – M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I – S) + (G – T) + (X – M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
- The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
- The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
- The Current Account balance (X – M) – positive if in surplus, negative if in deficit.
These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
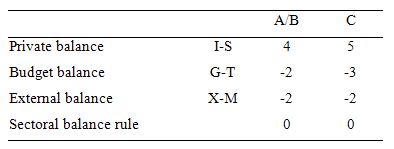
The following Table represents the three options in percent of GDP terms. To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.
The first two possibilities we might call A and B:
A: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending less than they are earn
B: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending more than they are earning.
So Option A says the private domestic sector is saving overall, whereas Option B say the private domestic sector is dis-saving (and going into increasing indebtedness). These options are captured in the first column of the Table. So the arithmetic example depicts an external sector deficit of 2 per cent of GDP and an offsetting budget surplus of 2 per cent of GDP.
You can see that the private sector balance is positive (that is, the sector is spending more than they are earning – Investment is greater than Saving – and has to be equal to 4 per cent of GDP.
Given that the only proposition that can be true is:
B: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending more than they are earning.
Column 2 in the Table captures Option C:
C: A nation can run a current account deficit with a government sector surplus that is larger, while the private domestic sector is spending less than they are earning.
The current account deficit is equal to 2 per cent of GDP while the surplus is now larger at 3 per cent of GDP. You can see that the private domestic deficit rises to 5 per cent of GDP to satisfy the accounting rule that the balances sum to zero.
What is the economic rationale for this result?
If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down.
The external deficit also means that foreigners are increasing financial claims denominated in the local currency. Given that exports represent a real costs and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.
A fiscal surplus also means the government is spending less than it is “earning” and that puts a drag on aggregate demand and constrains the ability of the economy to grow.
In these circumstances, for income to be stable, the private domestic sector has to spend more than they earn.
You can see this by going back to the aggregate demand relations above. For those who like simple algebra we can manipulate the aggregate demand model to see this more clearly.
Y = GDP = C + I + G + (X – M)
which says that the total national income (Y or GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
So if the G is spending less than it is “earning” and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income.
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 3:
When the government issues debt to match its budget deficit $-for-$ (or whatever currency unit is relevant) it also increases the net worth of the non-government sector.
The answer is False.
Within a fiat monetary system an understanding of the banking operations that occur when governments spend and issue debt allow us to appreciate what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a budget deficit without issuing debt?
Like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.
The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made. Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet). Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.
This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management.
When there are excess reserves there is downward pressure on the overnight interest rate (as banks scurry to seek interest-earning opportunities), the central bank then has to sell government bonds to the banks to soak the excess up and maintain liquidity at a level consistent with the target. Some central banks offer a return on overnight reserves which reduces the need to sell debt as a liquidity management operation.
There is no sense that these debt sales have anything to do with “financing” government net spending. The sales are a monetary operation aimed at interest-rate maintenance. So M1 (deposits in the non-government sector) rise as a result of the deficit without a corresponding increase in liabilities. It is this result that leads to the conclusion that that deficits increase net financial assets in the non-government sector.
What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.
The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).
There is no difference to the impact of the deficits on net worth in the non-government sector.
You may wish to read the following blogs for more information:
“The accumulated stock of government spending associated with continuous budget deficits can increase the risk of inflation faced by an economy- False”
Are you saying that an increased stock of net financial assets can NEVER increase the risk of inflation?
That seems very dubious to me. The accumulated stock of net financial assets can be deployed to extract a speculative return from the real economy. To some extent a speculation induced commodity price spike may be medium term deflationary if it causes an economic downturn but ultimately I think it has to be at least kept on the radar as a possibility that speculative price spikes could morph into an inflationary hiatus.
I think MMT is on very dodgy ground if it claims that financial assets can amount to an ever greater multiple of everything real that there is to buy and hope that that will have no malign consequence. Wealth managers will always ensure that by whatever means every dollar will extract a return.
Dear Stone (at 2013/03/17 at 23:47)
I think you misunderstood the intent of the question. It was about stocks and flows. There are financial asset stocks arising from deficits. But there can never be an accumulated stock of spending.
best wishes
bill
To my mind, stone has raised an interesting question. It is hard to believe that an ever increasing level of net financial assets in the sovereign currency, whether it is held by residents or non residents, does not have some important effect. However, I don’t understand it well enough to say what that effect might be. This is a big area of macroeconomics that I have not seen discussed satisfactorily.
Bill, am I understanding you right that if the wording were like this then it would be OK?:-
“The accumulated stock of NET FINANCIAL ASSETS RESULTING FROM government spending associated with continuous budget deficits can increase the risk of inflation faced by an economy-TRUE”
So the quiz question was more about precise use of language?
Perhaps the wording would need to be even more explicit to pass muster so:
“ALTERATIONS IN SPENDING BEHAVIOR CAUSED BY the accumulated stock of NET FINANCIAL ASSETS RESULTING FROM government spending associated with continuous budget deficits can increase the risk of inflation faced by an economy-TRUE”