It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
The IS-LM Framework – Part 2
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text during 2013 (to be ready in draft form for second semester teaching). Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.
Previous Parts to this Chapter:
Chapter 16 – The IS-LM Framework
[PREVIOUS MATERIAL HERE IN PART 1]
Figure 16.3 shows the derivation of the LM curve. From the money market diagram, the Points A, B and C represent equilibrium states where money demand equals money supply for different levels of income.
Each equilibrium point is thus a unique combination of income and interest rates.
We can translate this understanding to a new graph (right-hand panel) where national income (Y) is on the horizontal axis and the interest rate (i) is on the vertical axis.
If we trace the respective equilibrium points across into the income-interest space diagram we get a series of points that are consistent with money market equilibrium.
The intersection of all those points is the LM curve.
Note that at interest rate, i0, the LM curve is flat and becomes steeper at higher interest rates. What does that mean? The horizontal segment of the LM curve relates to the presence of the liquidity trap, which was named by English economist Dennis Robertson, who in the 1930s, worked closely with J.M. Keynes at Cambridge University.
The liquidity trap arises at some minimum interest rate (which could be zero) where everybody forms the view that the only direction for interest rates is up. The equivalent expectation is that everybody considers that capital losses will be incurred on bond portfolios because when interest rates rise, bond prices fall.
The result is that once interest rates reach this minimum level, all people will prefer to hold any new money in the form of cash instead of bonds.
In Chapter 15 of the The General Theory of Employment, Interest and Money, Keynes said (1936: 207):
There is the possibility … that, after the rate of interest has fallen to a certain level, liquidity-preference may become virtually absolute in the sense that almost everyone prefers cash to holding a debt which yields so low a rate of interest. In this event the monetary authority would have lost effective control over the rate of interest … Moreover, if such a situation were to arise, it would mean that the public authority itself could borrow through the banking system on an unlimited scale at a nominal rate of interest.
As we will see when we consider policy analysis within the IS-LM framework, the existence of a liquidity trap renders monetary policy ineffective as a counter-stabilising tool.
Monetary policy is characterised in this framework as the central bank manipulating the money supply and when the interest rate is at i0 in Figure 16.3, increasing the money supply would have no impact on interest rates or the price of bonds. In other words, monetary policy changes cannot alter the level of national income.
In a liquidity trap, a rise in the money supply leads to an equal rise in the demand for money and as a result the interest rate does not change. We will consider this in more detail later in the Chapter.
The LM curve is upward sloping at higher levels of income because as national income rises the demand for money increases and at each given money supply, the interest rate has to rise to ration the excess money demand and retain money market equilibrium.
The slope of the LM curve is steeper:
- The more sensitive the demand for money (transactions and precautionary motives) is to national income changes. Thus, small changes in national income lead to large changes in excess money demand at a given money supply level. The rise in interest rates to restore money market equilibrium, other things equal, has to be larger as a consequence.
- The less sensitive the speculative demand for money is to changes in interest rates. Thus, for a given excess demand for money, the interest rate increase that is required to restore money market equilibrium is larger.
While the horizontal LM curve (liquidity trap case) is one extreme, the other extreme is sometimes referred to as the Classical Case, which describes a vertical LM curve.
The Classical case arises from a demand for money function which is not sensitive to the interest rate. In other words, money is considered to be a means of exchange only and the speculative demand for money (which renders the overall demand for money sensitive to interest rates) is ignored.
In these cases, the demand for money shifts outwards when income rises and inwards when it fall. As a consequence there is only one national income level consistent with money market equilibrium for a given money supply and the LM curve is vertical.
In the Appendix to this Chapter we derive an analytical solution to the IS-LM framework for advanced studies, which show the impact of these two sensitivities (elasticities).
Shifts in the LM curve arise from changes in the money supply. Refer back to Figure 16.2, which showed that for a given money demand curve, interest rates fall when the money supply rises. The reasoning was that at a given money market equilibrium combination of interest rates and income, a rise in the money supply generates an excess supply of money, which requires interest rates to fall to stimulate the demand for money sufficiently to absorb the extra money.
In terms of the LM curve, this means that at higher levels of money supply, equilibrium interest rates will be lower at each income level which translates into a shift outwards in the LM. The opposite occurs when the money supply falls.
The LM curve can also shift if there is an autonomous change in liquidity preference, which means the money demand rises (falls) at each income level depending on whether the preference for liquidity rises (falls).
For example, if people become more pessimistic about the future they may use increased cash holdings as a haven from uncertainty. This will lead to an outward shift in the money demand curve so that for a given money supply, interest rates will be higher at each income level.
16.3 The IS curve
The IS curve shows all combinations of interest rates and income where the product (goods) market is in equilibrium. So unlike the simple income-expenditure model we developed in Chapter 12, the IS curve framework requires us to incorporate information about the money market (interest rates) in our understanding of equilibrium in the product market.
In Chapter 12 we developed the real expenditure model of income determination. From the National Accounting framework we know that total expenditure (E) in the domestic economy in any particular period can be expressed as:
(16.1) E = C + I + G + (X – M)
Equation (16.1) is identical to Equation (12.2). As it stands, Equation (16.1) is an accounting statement by dint of the definitions and sources of aggregate spending.
The equilibrium level of national income (Y) is determined by aggregate expenditure, such that Y = E. The task of Chapter 12 was then to understand the behaviour of each of the expenditure components in Equation (16.1) and theorise how they interact to determine national income.
At that stage we assumed that firms in aggregate plan a fixed volume of investment spending in each period. We were concerned at that stage of the text in tracing out the implications of changes in autonomous (exogenous) components of expenditure (investment, government, exports etc) on national income via the multiplier process.
However, in Chapter 2, we develop a more detailed model of investment spending, which allows us to take into account the impact on capital formation of changes in interest rates.
As a preview, we assume that rather than being exogenous, total investment spending is influenced, in part, by expectations of future economic conditions and the interest rate.
Business firms are continually forming expectations about future output. Firms have to make resource commitments (working capital, labour etc) well in advance of realisation (sales) and so the scale of production at any point in time reflects the guesses they make in a highly uncertain world.
Further, for given expectations about future sales and revenue, a firm’s investment decisions will also be influenced by the cost of capital goods, which, in turn, will be affected by the interest rate.
If interest rates rise, the cost of funds necessary to invest in new capital equipment rises and so marginal projects (relative to expected revenue) may become unprofitable. In other words, investment is likely to be an inverse function of the interest rate, other things being equal.
In other words, we might hypothesise that total investment is given as:
(16.2) I = b1 – b2i
where b1 is an autonomous component of investment and b2 is the interest-rate sensitivity of investment to interest rate changes.
The higher is b2, the more investment will decline (rise) for a given interest rate rise (fall).
The IS-LM framework retains the insight of Keynes that planned savings is a positive function of national income. A more detailed analysis of the General Theory would also reveal that Keynes considered that the interest rate might also influence consumption spending (via wealth impacts). Further, the purchase of consumer durables such as white goods, which might require access to consumer credit).
However, for now, to keep the argument simple, we assume that the interest rate only impacts on investment.
In Chapter 12. we assumed that firms in the economy are quantity-adjusters and so prices are fixed in the short-term. Figure 12.8 brought together the 450 aggregate supply curve with the aggregate demand curve (E). It showed that equilibrium national income occurs when the Aggregate Demand Function cuts the 450 line.
At this point, the aggregate demand expectations formed by the firms, which motivated their decisions to supply – Y* – are consistent with the planned expenditure – E* – by consumers, firms, government and the external economy.
Figure 16.4 augments Figure 12.8 by adding in the impact of Equation (16.2) – that is, allowing investment to be inversely impacted by interest rate changes.
Figure 16.4 Product market equilibrium and interest rate changes
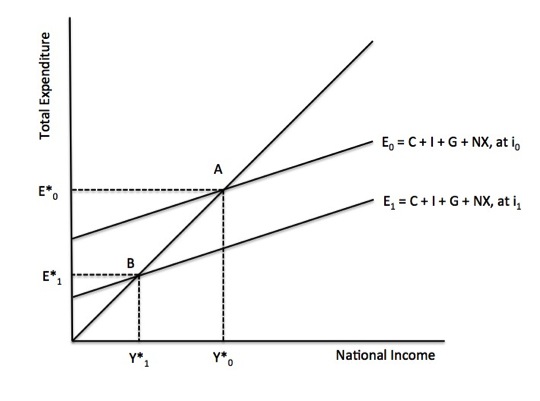
The total expenditure curve, E = C + I + G + NX is drawn from a given interest rate. The lower the interest rate (i0 < i1), the higher in investment (and total spending) at all income levels. As a consequence, the total expenditure curve shifts upwards.
When interest rates rise, the total expenditure curve would shift downwards, other things equal.
Point A in Figure 16.4 shows the product market equilibrium associated with an interest rate of i0. So we know that the combination of income level, Y*0 and interest rate level, i0 is an equilibrium combination in the product market.
What happens if the interest rate was to rise to i1? Total investment would decline at all income levels and the total expenditure curve would shift downward from E0 to E1.
The excess supply at the prior income level leads firms to cut back output and employment and national income falls. A new product market equilibrium occurs when E*1 = Y*1.
So the combination of income level, Y*1 and interest rate level, i1 is an equilibrium combination in the product market.
We thus have two combinations of interest rates and income levels which are consistent with product market equilibrium. Clearly we could trace out the impact of many interest rate changes and thus many equilibrium combinations of interest rates and income.
The IS curve is the line that joins all the equilibrium combinations of interest rates and national income. Figure 16.5 shows this derivation.
Figure 16.5 The derivation of the IS curve
GRAPH TO COME.
[TO BE CONTINUED IN PART 3]
Conclusion
PART 3 next week – Policy Analysis and Critique
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
Monday’s Blog
I am going to be in some very remote locations for the next three days (Kakadu National Park) and I might not get to file a blog on Monday. We will see.
That is enough for today!
(c) Copyright 2013 Bill Mitchell. All Rights Reserved.

Here are some more comments.
“The liquidity trap arises at some minimum interest rate (which could be zero) where everybody forms the view that the only direction for interest rates is up. The equivalent expectation is that everybody considers that capital losses will be incurred on bond portfolios because when interest rates rise, bond prices fall.”
I heard that many times, but still: a $100 dollar bond with an interest rate of zero held to maturity at rising interest rates incurs no capital loss. Depending on accounting rules a temporary loss will show up but if you are not forced to make position than there is no problem. Mentioning Ponzi finance in the IS/LM chapter is probably out of bounds, but I think that this would be where Minsky comes in to support Keynes.
“In a liquidity trap, a rise in the money supply leads to an equal rise in the demand for money and as a result the interest rate does not change. We will consider this in more detail later in the Chapter.”
A rise in the money supply also leads to an equal rise in the demand for money when you have a vertical supply curve (like in your previous post), but here the interesting thing to note is that it is absorbed fully by the speculative motive.
“E = C + I + G + NX”
The IS/LM model deals with a closed economy, of course.
best,
Dirk