It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
Analytical appendix for NIPA Chapter 3
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to publish the text sometime in 2013. Our (very incomplete) textbook homepage – Modern Monetary Theory and Practice – has draft chapters and contents etc in varying states of completion. Comments are always welcome. Note also that the text I post here is not intended to be a blog-style narrative but constitutes the drafting work I am doing – that is, the material posted will not represent the complete text. Further it will change as the drafting process evolves.
The Table of Contents for the first draft, which is nearly completed, currently lists Chapter 3 as National Income Accounting, with a section 3.7 Using the NIPA Framework to Model the Macro Economy. The status of this section might change but the content aims to present some analytical terminology that is used in the specification of macroeconomic models which the student encounters throughout the textbook.
The section (or subsection) will cover basic algebra, manipulation of equations, solving simple linear models, consideration of graphs, and some essential tools that help an applied macroeconomist assess data trends etc.
Today, I am adding to the material already developed which is currently available as Chapter 3 Draft, Section 3.8.
The snippets I develop here will be integrated into the draft for further assessment. The ambiguity of the numbering reflects the transient status of these sections.
In this section we present some analytical terminology that is used in the specification of macroeconomic models and which you will find throughout this book.
The level of mathematics that will be used throughout this book is no more sophisticated than the typical material that a student would encounter in the second-half of their secondary school studies. The most advanced analysis we employ is simultaneous equation techniques and some simple calculus. For the most part, the mathematics is confined to algebraic representations of the behavioural theories and/or accounting statements that we advance and some simple solution exercises to determine the unknown aggregates we are interested in.
The practical material accompanying the analytical text will also provide a step-by-step sequence to mastering the techniques required.
We recognise that mathematical techniques are commonly used within the social sciences and that students will gain confidence in dealing with the standard conceptual and empirical literature in economics and more broadly if they develop some formal modelling skills in addition to the deep understanding that we hope to engender.
Overview
In macroeconomics we often deploy symbols to represent real world variables of interest, such as real GDP, consumption, investment. In this case, while the symbols can have an abstract meaning (for example, Y is real GDP) they will also usually have, given the nature of economics, some quantitative analogue (for example, in the September-quarter 2013, real GDP in Australia was estimated to be $A387,031 million).
The use of symbols also allows us to deploy the mathematics to analyse relationships between these variables. In that context, we apply the basis rules of algebra to conduct our analysis.
In Chapter 1, the concept of a model was introduced. A macroeconomic model expresses our theoretical conjectures about the connections between the main macroeconomic variables such as employment, output and inflation.
A model is a generalisation about the way the system functions or behaves. It could easily be a narrative statement such as – a household will consume a proportion of their income after tax (disposable income). That theoretical statement might then be examined for its empirical relevance but will also stimulate further theoretical work trying to provide an explanation for that conjectured behaviour.
In economics, like other disciplines that use models, the narrative statement might be simplified with some mathematical statement involving symbols. In this context, the models will be represented by a number of equations (which could be one), which describe relationships between variables of interest.
We use letters (such as, Y) or Greek symbols (such as, α) to denote elements in the model. A variable can take on different values in different time periods. Other elements in the model might be considered to be constant over time.
In the context of economic modelling, a variable is some measured economic aggregate (like consumption or real output) and is denoted by some symbol that makes sense. The correspondence between the shorthand symbol and the variable is not always intuitive but conventions have been established, which we retain in this textbook.
So Y is often used to denote real GDP or National Income (but it can also be used to denote total output). C is usually used to denote final household consumption and I total private investment. X is typically used to denote exports and M imports although in some cases M is used to denote the stock of Money. In this text, M is exclusively used to denote imports.
There are several types of variables used in macroeconomic models:
- Endogenous variable – is a variable whose value is determined by the solution to the model.
- Exogenous or autonomous variable – is a variable whose value is given in advance of solving the model.
- Dependent variable – is a variable whose value is dependent of the values of other variables.
- Independent variable – is a variable whose value determines (wholly or partly) the value of some related dependent variable.
Variables are related by way of equations which express the structure of the macroeconomic model. A macroeconomic model can contain one or more equations depending on the scope of the analysis. Some large and complex models have thousands of equations.
Usually a variable that we seek to explain is written on the left-hand side of the equals sign (=) and is then expressed in terms of some other variables on the right-hand side of the equals sign, which we consider are influential in explaining the value and movement of the left-hand side variable of interest.
The relationship between the variables on the right- and left-hand side of the equation is described in terms of some coefficients (or parameters).
For example, y = 2x is an equation which says that variable y is equal to 2 times variable x. The equals sign (=) tells us that the left-side of the equals sign is of the same magnitude as the right-side (that is, an equation has equal left and right sides).
You solve an equation by substituting values for the unknowns. The number 2 in the equation is called a coefficient which is an estimate of the way in which y is related to x.
So if x = 1, then we can solve for the value of y = 2 as a result of this equation.
A coefficient can also be called a parameter – which is a given in a model and might be estimated using econometric analysis (regression) or assumed by intuition. In that context, the coefficient’s value is unknown.
For example, we might have written the above equation as y = bx, where b is the unknown coefficient. You will note that we would be unable to “solve” for the value of y in this instance even if we knew the value of x. In the case above where we said x = 1, then all we could say that y = b. We would thus need to know what b was before we could fully solve for y.
There are several types of equations that are used in macroeconomic models:
- Identity equation – is an expression that is true by definition (usually relating to an accounting statement). For example, we will see that GDP is equal to the sum of the expenditure components, which is true as a result of the way we set up the national accounts. In mathematics, the symbol ≡ to denote an identity relationship. In this book, we will typically just use the standard equals sign = to an identity and rely on the context to differentiate between an accounting identitity and another type of equation.
- Behavioural equation – captures the hypotheses we form about how a particular variable is determined. These equations thus represent our conjectures (or theory) about how the economy works and obviously different theories will have different behavioural equations in their system of equations (that is, the economic model).
- Equilibrium equation – is an expression that captures a relationship between variables that defines a state of rest.
While the above example (y = 2x) was easy to solve once we knew the value of x, sometimes it is useful to have models where we cannot solve for numerical values of the unknown variables of interest but we can simplify the equations to show the structure of the model in terms of what is important to advance our understanding of the relationship between our aggregates.
Basic rules of algebra
You will need to learn some basic algebraic rules that are used to manipulate equations and solve for unknowns of interest. Often you will need to rearrange a given equation in order to determine the solution for the variable of interest.
Rule: Addition and subtraction
In an equation y = x, then we know the equivalent expression is y ± z = x ± z. So y = x is equivalent to y + 2 = x + 2.
In general, what we add to or subtract from one side of the equation we have to add to or subtract from the other side to maintain the equality.
We can also substitute an expression from one equation into another and maintain equivalence.
For example, we might have y = 2x, and x = 6z. In this case, it is equivalent to write y = 2(6z) = 12z.
Rule: Multiplication and division
In an equation y = x, then we know the equivalent expression is 3y = 3x or y/3 = x/3. If we multiply or divide the left-hand side of the equation by a variable (or more complex algebraic expression) then we have to multiply or divide the right-hand side of the equation by the same variable (or expression).
A more complex example is y = 6x and x = z/2. In this case, y = 6(z/2) = 3z.
Model solutions
In a system of equations, the values of some variables are unknown and are only revealed when we “solve” the model for unknowns.
So if we have these two equations, which comprises a “system”:
(1) y = 2x
(2) x = 4
Then x is a pre-determined variable (with the value 4) and is thus exogenous. You do not know the value of y in advance and you have to solve the equations to reveal its value – so it is endogenous. It is determined by the solution to the system.
To solve this system we substitute the value of x in Equation (2) into Equation (1) so we get:
y = 2 times 4
y = 8
So the solution of a system merely involves substituting all the known values of the coefficients (in this case the 2 on the x) and the exogenous variables (in this case x = 4) into the equations that depict the endogenous variables (which in this case is only Equation (1) but there will typically be multiple endogenous variable equations).
In real modelling it becomes very complicated as to which variables can be considered endogenous and which are truly exogenous. At the extreme, everything might be considered endogenous and then things get mathematically complex and there is a whole body of theory in econometrics relating to the identification problem, which is well beyond this textbook.
A simple macroeconomic model
An example of an indentity (which is true by definition) is the famous national income equation depicting aggregate demand and output, which we consider in Chapter X:
Y = C + I + G + X – M
Note that in strict terms we write an equation that is an identity using the identity sign (three parallel horizontal lines) instead of the equals sign (two parallel horizontal lines). That distinguishes it from a behavioural equation which is always expressed using an equals sign (=).
This identity is also an equilibrium condition in the simple national income model but it provides no information about how the right-hand side variables behave, what they, in turn depend upon. To advance that understanding we form theories about the determinants of these variables.
These theories are expressed in behavioural equations. An example of a behavioural equation, which captures a conjecture about the way variables relate, is the simple Consumption function:
C = C0 + cYd
which says that final household consumption (C) is equal to some constant (C0) plus some proportion (c) of final disposable income (Yd). The constant component (C0) is the consumption that occurs if there is no income and might be construed as dis-saving.
Note that subscripts are often used to add information to a variable. So we append a subscript d to our income symbol Y to qualify it and denote disposable income (total income after taxes).
We also use subscripts to denote time periods when we are considering a variable over time. So Yt indicates we are considering the value of Y at time period t. Similarly, Yt-1 refers to the value of Y at time period t-1, where the lag (the -1) depends of the periodicity of the data. If we were using quarterly data, then t-1 would be last quarter and so on.
In macroeconomics, some behavioural coefficients are considered important and are given special attention. So the coefficient c in the Consumption function is called the marginal propensity to consume (MPC) and denotes the extra consumption per dollar of extra disposable income. So if c = 0.8 we know that for every extra dollar of disposable income that the economy produces, 80 cents will be consumed.
The MPC is intrinsically related to the marginal propensity to save (MPS) which is the amount of every extra dollar generated that is saved (after households decide on their consumption). So the MPS = 1 – MPC by definition.
The importance of MPC is that is one of the key determinants of the expenditure multiplier (more about which later). We will consider this in Chapter X when we discuss the expenditure multiplier.
We have already introduced the distinction between an exogenous (pre-determined or given) variable and an endogenous variables (which are determined by the solution to the system of equations).
An exogenous variable is known in advance of “solving” the system of equation. We take its value as given or pre-determined. We might say, by way of simplification, that government spending (G) in the above model is equal to $100 billion which means that its value is known and not determined by the values that the other variables take or are solved to.
The two equations (the identity and behavioural equation) noted above form a macroeconomic system. This is, of-course, a very simple system. For the sake of exposition, we might assume the economy is closed which means there are no exports or imports. In that case, the national income identity becomes Y = C + I + G.
We also assume there is no taxation in the model, so that disposable income is equal to total income (Y).
The model is now:
(3.X1) Y = C + I + G
(3.X2) C = C0 + cY
For simplicity, we will assume that I and G are exogenous and their values are known in advance. The remaining two variables Y and C become endogenous and their values are dependent on the solution to the model.
How do we solve for Y?
We substitute (3.X2) for C in (3.X1) such that:
(3.X3) Y = C0 + cY + I + G
We can now re-arrange this (noting we have Y on both sides) by subtracting cY from both sides as per our algebraic rules. This gives:
(3.X4) Y – cY = C0 + I + G
You will note that there are only predetermined variables (knowns) on the right-hand side now.
We can re-arrange this further:
(3.X5) Y(1 – c) = C0 + I + G
This uses the rule relating to factorisation where Y is a common factor on the left-hand side. Note that Y(1 – c) = Y – cY.
We can then invoke the rule whereby we divide both sides by (1 – c) to isolate (or solve) for Y on the left-hand side. Thus:
(3.X6) Y = 1/(1 – c)[C0 + I + G]
So in words, the equilibrium value of Y is some function of the autonomous variables in the model C0 + I + G.
We call Equation (3.X6) the reduced-form solution of the model, where there are only exogenous or predetermined variables on the right side and an unknown variable on the left-hand side of the equation.
In a macroeconomic model, all the endogenous variables can be expressed in reduced-form. So in the example above, our solution for consumption would be:
(3.X7) C = 1/(1 – c)[C0 + I + G]
Make sure you can derive the steps that we would take to get this solution.
The reduced-form of the system allows us to conduct sensitivity analysis, which involves changing the values of the exogenous variables or the coefficients (in this case, the MPC) and analysing the impact on the endogenous variables in the model.
As an example, what would be the impact of an expansion in government spending G on national income Y? Note that we assume the other exogenous variables are unchanged.
From Equation (3.X6), we know that when G = G0:
(3.X6a) Y0 = 1/(1 – c)[C0 + I] + 1/(1 – c)[G0].
Note, to make the manipulation clear, we have separated G from I and C0.
If G rises to G1, then:
(3.X6b) Y1 = 1/(1 – c)[C0 + I] + 1/(1 – c)[G1].
So the change in Y = (Y1 – Y0) is the difference between (3.X6b) and (3.X6a):
(3.X6c) (Y1 – Y0) = 1/(1 – c)[G1 – G0].
To simplify our notation, we will usually denote the change in a variable using the Greek symbol Δ. So Equation (3.X6c) would be written as:
(3.X6d) ΔY = 1/(1 – c)ΔG
where the time span that Δ denotes is provided by the context.
We can then express Equation (3.X6d) as:
(3.X6e) ΔY/ΔG = 1/(1 – c)
where the right hand side is known as a multiplier because it tells us the magnitude of the change in Y for a unit change in G. We will examine multipliers in more detail in Chapter X.
[BIT MORE HERE NEXT WEEK – on SHIFTS IN EQUILIBRIUM ETC]
Graphical depiction of macroeconomic models
We will also express our theories in graphical terms, which are an alternative to mathematical representation. Here are three ways to express the same theoretical idea.
1. Household consumption rises proportionately with disposable income but the proportion is less than one.
2. C = C0 + cYd, where 0 < c < 1 and C0 is a constant (fixed value). The less than sign (<) tells us that the MPC lies between the value of 0 and 1, that is, it is positive but less than 1.
3. Graphical form:
If C0 = 100, and c = 0.8, and Yd = 1000 then total consumption would be 900. We could have solved the equation C = C0 + cYd by inserting the known values of the parameters and explanatory variable (in this case disposable income) into the equation and solving it.
Thus:
C = C0 + cYd = 100 + 0.8 x 1000 = 900.
You can also see that by tracing a vertical line from where Disposable income equals 1000 up to the graph line and then tracing across the vertical axis we derive the value of Consumption by where that line crosses the vertical axis.
It was stated that the slope of the line is the Marginal Propensity to Consume (c). How do we derive a slope of a line and what does it mean? In Chapter 3 we will deal with applications of the slope of a line when we study the principle of the spending multiplier.
In general terms the following will be useful.
SIMPLE TOOLS OF CALCULUS WILL BE DEVELOPED HERE AND A GRAPH TO BE INSERTED HERE.
We recognise that different students have different ways in which they learn and accumulate knowledge. Some prefer the mathematical approach while others prefer the graphical approach. Others still learn better through reading the written word, even though that form of communication is prone to interpretative issues. In that regard, all the essential material in the text will be presented in all three ways (sometimes the mathematics will appear in the Annexe of the relevant chapter sometimes within the main body of the text.
3.X Annual average growth rates
Economists often are required to compute how fast the economy (or some other aggregate) is growing. In this section, we learn how to compound an average compound growth rate. We assume that you understand the concept of a compound growth rate.
In 1960, real GDP in Australia was $249,083 million and it had grown to $1,508,267 million by 2012. To calculate the average annual compound growth rate over this 52-year period, we need to utilise some simple algebra and deploy the notion of a compound growth rate.
We know that
where, using the example in question, Y1 is real GDP in 2012; Y0 is real GDP in 1960; r is the average compound growth rate; and t is the number of periods that we are compounding over, in this case 52 years.
The task is to solve for the unknown r:
Table 5.A shows the calculation steps and you can paste the data into a spreadsheet and see if you can derive the same results by replicating the solution steps in Figure 5.A2. The calculations show that the annual average compound growth real GDP growth rate for Australia between 1960 and 2012 was 3.52 per cent.
You can use this formula for any period or data frequency (for example, month, quarter, year) by substituting the appropriate information into the calculation.
Figure 5.A1 Compound growth rate calculations

[MORE TOOLS AND TECHNIQUES NEXT WEEK]
Conclusion
I am now going back through the first draft and editing, adding and refining sections.
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
That is enough for today!
(c) Copyright 2013 Bill Mitchell. All Rights Reserved.

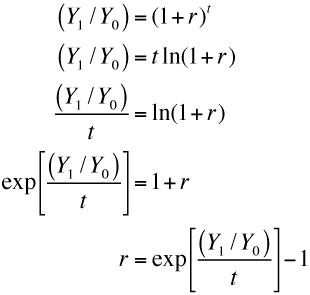
Bill, if I may, I would like, once again, to argue for reconsideration of the traditional terminology that has become prevalent in some sciences, in this case, economics. I realize that I am no doubt on a hiding to nothing but I’ll give it a go anyway. At least, the textbook could alert the students to the alternative. You could do this in an appendix or the like, and I would expect you would have to convince Randy that this was a viable addition to the enterprise on which you two are working.
When you mention models, you almost immediately afterwords show that you are really talking about theories. And the problem with talking about theories and calling them models, I believe, can lead to some degree of conceptual confusion and possible lack of a certain kind of deep understanding. While the point of view I am going to espouse is not the only way of doing this, it has I think the benefit of clarity for the student first coming to this kind of debate. The perspective I am elaborating is that consistent with model theory
First, I would define a theory as a set of sentences, or propositions if you prefer, but let me stick to sentences, about a particular phenomenon that provides an explanatory framework. It is a kind of explanation. That is, a theory is a kind of linguistic entity, which must satisfy certain grammatical requirements.
A model, on the other hand, is a non-linguistic structure, physical or conceptual, in which the theory is true. If a theory has no model, it is incoherent or inconsistent. A false theory should have no corresponding model. The tricky bit here is that one has to use language to talk about models, which are not linguistic. But if you think of a theory as being linguistic and a model as non-linguistic, this potential misunderstanding can be avoided.
A potential difficulty arises when you discuss computer simulations. Are computer simulations, or programs, theories or models of theories? There is no consensus on this, but my point in bringing this up is that on your approach, the question can’t arise because a computer program/simulation will be considered to be a model of the empirical phenomenon. And since your use of “model” is virtually equivalent to my term, “theory”, computer programs automatically become theories. But are they?
There is a certain clarity that comes almost automatically, I think, when you distinguish between “theory” and “model” of a theory that cannot arise when you equivocate in the use of the two terms, as I believe you and Randy are doing. I am aware that bringing this distinction into your discussion, which contrasts with the way the literature is written, brings its own problems. So, I can’t judge whether the problems that might be created by altering the way you discuss economic theories (your models), which would be inconsistent with a good bit of the literature, would be compensated for by what I feel would be a considerable clarification of the conceptual domain that you will be dealing with in your textbook. In the end, only you and Randy can do that.
As you yourself will know, I have considerably simplified the subject, but my intention is only to highlight it. A good reference for this way of looking at the subject is the ‘Critical Introduction’ and ‘Afterword’ of The Structure of Scientific Theories, 2nd ed, by Fred Suppe. Although it is not recent, it is not thereby past its sell by date, as it were.
A clarificatory note:
I realize that when you say things like, we are going to model the macro-economy, when it comes to the perspective I am suggesting, the question may well arise: how could this be expressed in my terms in as clear a way as this is in yours. I would say: we are going to construct a theory of the macroeconomy that will have as one of its models, the real economy; and this possesses a distinct advantage over the neoclassical theory, which does not have the real economy as one of its models, though its adherents claim that it does.
Every theory has more than one model. But an empirically relevant scientific theory must have something about the real world as one of its models, or it is scientifically otiose.
You have around 26 days then Bill. Good luck with that.
Addendum:
Apologies for this addition but I thought it might help. In my scheme, it is theories that are true or false, not models. Models just are. Just as the real economy is not something that is true or false. It just is. In my scheme, I would argue that this relationship is patently clear, whereas in yours, where you equivocate between “theory” and “model”, this relationship is somewhat opaque.
I know that there are issues surrounding the concept of truth itself, but I take them to be resolved in Gupta and Belnap’s The Revision Theory of Truth.
Just a little observation regarding the multiplication and division rule: maybe it would be a good idea to remind readers that denominators in a fraction cannot be zero. In other words:
x/K = y/K (provided K different from 0)
Magpie,
It might be better to say that for any x, y, x/y is defined except when y=0, or provided y not-= 0 when working within the real number system. That is, when the denominator in a fraction is zero, the fraction is undefined, by definition. This means that 0/0 is undefined, too. When economists are dealing with money or currencies, they are working within the real number system.
This division by zero rule holds unless you are dealing with limit functions where L’Hospital’s rule applies. (Stigler argues that this is really Bernoulli’s rule but is known as L’Hospital’s rule because Bernoulli sold the rights to the equation to L’Hospital.)