It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
Growth and Inequality – Part 3
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to publish the text sometime around mid-2014. Our (very incomplete) textbook homepage – Modern Monetary Theory and Practice – has draft chapters and contents etc in varying states of completion. Comments are always welcome. Note also that the text I post here is not intended to be a blog-style narrative but constitutes the drafting work I am doing – that is, the material posted will not represent the complete text. Further it will change as the drafting process evolves.
Previous blogs in this series:
Chapter X Growth and Inequality
X.2 Keynesian growth theories – Harrod-Domar
[PREVIOUS MATERIAL HERE]
[WE LAST CONSIDERED THE DUAL NATURE OF INVESTMENT WHICH WAS STRESSED IN DOMAR’S 1947 ARTICLE “EXPANSION AND EMPLOYMENT”. WE HAD DERIVED THE RELATIONSHIP BETWEEN INVESTMENT SPENDING AND GROWTH IN PRODUCTIVE CAPACITY. TODAY WE CONSIDER THE DEMAND SIDE IMPACTS OF INVESTMENT AND BRING THE TWO TOGETHER TO DEFINE THE GROWTH IMPERATIVE – IT SHOULD BE FUN]
X.x1 The demand contribution of investment
The growth in productive capacity flowing from the increased investment expenditure places requirements on the growth in aggregate spending if the productive capacity is to remain in use. By how much does actual output have to grow to ensure there is no idle capacity? We will call this the required rate of real GDP growth?
Consider a simplified version of the the expenditure-income model we discussed in Chapter 12. We will assume the economy is closed (which makes very little difference to the basic insights).
Aggregate demand is the sum of C + I + G and actual real output increases in line with the growth in aggregate demand. The marginal propensity to consume (c) tells us the extra consumption per extra dollar of real income (output) and we assume a simple consumption function of the form, C = cY. The marginal propensity to save (s) = 1 – c
We assume no taxation, so that the expenditure multiplier is equal to 1/(1 -c). Given that c = 1 – s, the multiplier can also be written as 1/s.
The exogenous components of aggregate demand are investment (I) and government spending (G). We assume that G does not add to productive capacity, an assumption we will relax in a later section.
The change in output or income is given as:
(X.9) ΔY = (1/s)[ΔI + ΔG]
Equation (X.9) shows that for every dollar of extra investment or government spending, total output (Y) rises by the value of the multiplier.
While investment and government spending add to aggregate demand identically, the implications for growth are somewhat different under our simplifying assumption that government spending does not add to productive capacity.
Compare Equation (X.9), which concentrates on the growth in effective demand to Equation (X.8), which showed the growth in potential output (or total productive capacity), ΔYp = θI
If there was no government sector, then Equation (X.9) simplifies to ΔY = (1/s)ΔI. In that form, you can see the dual characteristics of investment. Equation (X.8) shows the supply-side impact (expanding productive capacity) whereas Equation (X.9) shows the demand-side impact (adding to aggregate demand).
The problem of growth (apart from the modern focus on environmental issues) is that the determinants of growth in aggregate demand are different to the determinants of the growth in productive capacity and there is no natural tendency for the outcomes to be matched.
If aggregate demand is constant, then equilibrium income will remain unchanged. But now we can appreciate that equilibrium income does not imply full employment. An economy with a constant flow of investment expenditure and stable national income, will, other things equal, experience a rising output gap and unemployment. We demonstrate that problem in Section X.x2.
X.x2 How much does aggregate demand have to rise to absorb growth in capacity?
If we assume that full employment of both labour and capital will occur when actual output is equal to potential output then we can define the condition that will ensure the economy remains on a full employment growth path.
Clearly, the growth in actual output (and hence aggregate demand) has to equal the growth in productive capacity created by the flow of investment spending. Equation (X.8) defined the the change in productive capacity, whereas Equation (X.9) defined the growth in actual output. For simplicity, assume no government spending. Thus equating Equation (X.8) and (X.9) gives:
(X.10) (1/s)ΔI = θI
The left-hand side of Equation (X.10) describes the aggregate demand impact of investment and the right-hand side describes the aggregate supply impact of investment.
We can re-arrange Equation (X.10) by multiplying both sides by the marginal propensity to save (s) and dividing both sides by I to give:
(X.11) ΔI/I = sθ
ΔI/I is the growth in investment that will ensure there is no idle productive capacity. Adding government spending does not alter this basic result but provides more options for an economy.
This result also has implications for the way we think of the relationship between saving and investment. Many people think that saving provides the funds for investment. As we saw in Chapter 22, investment brings forth its own saving by increasing national income.
Reflecting on the results and understandings that we have derived in this Chapter, we can conclude that even if all the saved income was invested, this would be insufficient to prevent unemployment.
In his 1947 article, Evsey Domar wrote (pp 38-39) that the “answer to the problem of unemployment lies of course in a growing income … There is nothing novel or startling about this conclusion … the construction of a new factory has a dual effect: it increases productive capacity and it generates incomes” (emphasis in the original).
[Reference: Domar, E. (1947) ‘Expansion and Employment’, American Economic Review, 37(1), 34-55.]
Reflecting on this, Domar concluded that (p.41):
… the maintenance of a continuous state of full employment requires that investment and income grow at a constant annual percentage … rate equal to the product of the marginal propensity to save and the average … productivity of investment.
This conclusion describes Equation (X.11), which is derived in Domar’s 1947 article. He then drew out the implications of that result by saying that it (p.42):
… shows that it is not sufficient … that savings of yesterday be invested today, or, as it is often expressed,that investment offset saving. Investment of today must always exceed savings of yesterday. A mere absence of hoarding will not do. An injection of new money (or dishoarding) must take place every day. Moreover,this injection must proceed, in absolute terms, at an accelerated rate. The economy must continuously expand.
This result is based on a very simple closed economy without government. As we will see in the quantitative example in the next Section, the addition of government spending provides an economy with more flexibility to ensure the growth in actual output maintains pace with the growth in productive capacity.
The result also has implications for modern debates regarding the apparent conflict between the economic growth imperative and the capacity of the natural environment to absorb that growth. With an expanding population (and labour force) and increased productive capacity, we cannot escape from the conclusion that national income and thus spending has to grow over time, if material standards of living are to be (at least) maintained and for poorer nations increased.
However, the environmental constraints place clear restrictions on the form that such growth has to take. While that debate is beyond the scope of this section, we urge students to reflect on these two imperatives in a unified way rather than treating them as separate areas of enquiry.
X.x3 Quantitative example of the Domar investment duality
Consider the economy outlined in Table X.1 with quantifies the simple expenditure-income model we discussed in the previous section.
The marginal propensity to consume (c) is 0.8 and the tax rate is zero, which means the expenditure multiplier is equal to 5. The marginal propensity to save is thus equal to 0.2, which means that for every extra dollar a household receives 80 cents is consumed and 20 cents is saved. We also assume a simple consumption function of the form, C = cY.
We will assume the output-capital ratio (θ) is 0.25, which means that for every $4 worth of productive capital, the potential real GDP is equal to $1. The capital stock increases each period by the flow of investment spending, which increases the potential GDP by 0.25 times I.
From Equation (X.8), the change in productive capacity is equal to ΔI times θI, where Δ simply denotes the change between periods.
The Output Gap is the difference between actual GDP and potential GDP and is a measure of the idle productive capacity in the economy. If we modelled the labour market in this example, the idle capacity would reveal itself as unemployment. We thus conclude that when the economy is producing at capacity, there is full employment of labour. We will return to this issue presently.
The final column denotes the Change in Exogenous Spending Required, which denotes the chage in aggregate demand that will maintain a zero output gap and sustain full employment. The aggregate demand boost could come from either increased I or G, and the implications for the growth process differ depending which is the source of the stimulus. The required change in spending is calculated by dividing the change in productive capacity by the expenditure multiplier.
So if we started from a fully employed position and potential output rose by $25, then real output has to rise by $25 for the output gap to remain at zero. A $25 increase in GDP with a multiplier of 5, requires an exogenous boost in aggregate demand of 5.
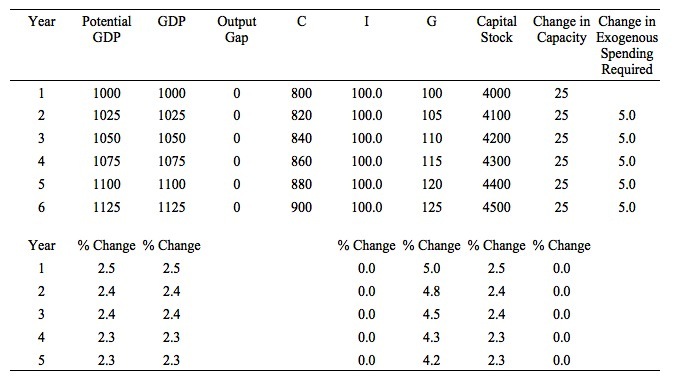
In Table X.3, the expenditure flows (C, I and G) are constant over the six years shown, which means that real GDP is also constant at $1000.
However, the output gap increases each year by $25 and by the end of Year 6 it is $125. Why has that outcome occurred? Note that the constant investment each year means that the capital stock is rising by $100 each year and the potential GDP is rising by $25 each year.
This demonstrates that while investment is adding $100 to aggregate demand each year, it is also adding $25 to productive capacity each year, which has to be absorbed by spending in the next period or else the economy will endure idle capacity and unemployment.
In Table X.3, aggregate demand growth is insufficient to match the growth in capacity.
Another way of seeing this is to examine the growth rates of the aggregates that are shown in the lower panel of Table X.3. You can see that the growth in capacity outstrips the zero growth in actual GDP. To test your understanding, why is the growth in potential GDP (and the capital stock) declining each year?
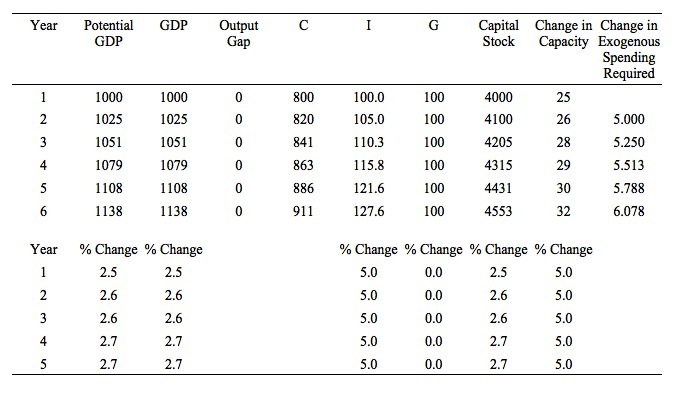
Consider Table X.4 which shows government spending increasing by $5 each period which is the required change in exogenous spending. Now the actual economic growth is sufficient to absorb the growth in productive capacity (being generated by the constant flow of investment each period) and the economy stays at full employment.
Note that the capital stock is increasing at the same rate as in the example in Table X.3. This is because investment is constant.
Now consider Table X.5, which shows investment increasing each period by the amount required to keep the output gap closed. You will notice that the capital stock is now increasing faster than before as is potential GDP. The actual output growth required to keep the output gap closed is also much higher than previously and the change in aggregate demand each period is higher when investment is growing than when rise in government spending closed the gap.
Why is that?
The answer lies in the dual characteristics of investment that we have been considering in this section. Investment adds to aggregate demand in the current period but also to productive capacity next period. The growth in aggregate demand has to be that much larger next period to absorb the extra productive capacity created by the investment in this period.
You can see that in Table X.5, the growth in capacity shown in the lower panel is equal to 5 per cent. You should verify that this is equal to the result obtained in Equation (X.10).
We should be careful though not to assume that government spending does not add to productive capacity. We are abstracting from the impact of government spending on the potential of the economy in this simplified example. When we example the social model of productivity growth in a later section of this Chapter we will see how important government spending is for enhancing the productive capacity of the economy.
[NEXT WEEK I WILL TIE THIS BACK INTO THE HARROD’S NOTIONS OF WARRANTED AND NATURAL RATE OF GROWTH AND THE ANALYSIS OF INSTABILITY – THEN I WILL DISCUSS DETERMINANTS OF PRODUCTIVITY AND INTRODUCE THE SOCIAL MODEL OF PRODUCTIVITY WHICH CHALLENGES THE MAINSTREAM CONCEPTION OF THE DETERMINANTS OF PRODUCTIVITY]
References
Domar, E. (1947) ‘Expansion and Employment’, American Economic Review, 37, 34-55.
Harrod, R. (1939) ‘An Essay in Dynamic Theory’, Economic Journal, 49, 14-33.
Conclusion
CONTINUING NEXT FRIDAY.
Saturday Quiz
The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:
That is enough for today!
(c) Copyright 2013 Bill Mitchell. All Rights Reserved.

Bill,
I think you have to be more careful on the environmental stuff. In my experience students often come away from this thinking that income growth is at odds with environmental sustainability. This is also the general narrative on the Green Left, as I’m sure you know.
But as you say: it’s all about the FORM the growth in income and productive capacity take. If you build a smog factory this will generate income but so too will a solar factory. I think it might be worth adding a paragraph making this clear to dispel this myth. It has done such a great deal of damage amongst the Greens.
Dear Bill
There is replacement investment and expansionary investment. The first is simply necessary to maintain the capital stock at the current level, to compensate for depreciation. The second increases the capital stock. However, not all expansionary investment is the same. it depends on whether there is population growth or not. If there is population growth, then some expansionary investment is required simply to avoid capital dilution. The implication of this is that population growth requires demographic investments. A further implication is that, with population growth, an economy has to grow at a faster rate than the rate of population growth simply to avoid capital dilution.
Let’s illustrate this. We have a city with 2 million residents and one bus per 2,000 residents. So, it has 1,000 buses. Let’s assume that the useful life of a bus is 10 years. Then the city has to replace 100 buses each year, at least on average. Now we assume that the city’s population grows by 20,000 people each year. To maintain the ratio of one bus per 2,000 residents, the city has to buy 110 buses each year, 100 to replace old buses and 10 to accommodate population growth. Those 10 additional buses are a demographic investment. It is a term that I never encountered in English, but which I picked up from the French social scientist Alfred Sauvy. Notice that in our example the population grows by 1% per year but the investment by 10%. That’s why an economy has to grow faster than the population.
Let’s assume that there is a population of 100 with a GDP of 1000 and a capital stock of 3000. Technology is constant and each year the replacement investment is 10% of the capital stock. As a result, consumption is 700 and investment 300. Now let’s add one person to the population. Population is now 101. GDP will have to be 1028, consumption 707, replacement investment 300, expansionary investment 21, in order to increase consumption by 7 with a capital/output ratio of 3 to 1.
The standard of living is determined by consumption. Investments are only means to enable consumption. If the standard of living is to remain the same, then an economy has to grow faster than its population. In our example, the population grew by 1% but the economy had to grow by 2.8% while total consumption increased by 1% and per capita consumption remained the same.
Both examples are simplifications, but I think that I demonstrated that, because of demographic investments, economic growth has to be faster than population growth if the standard of living is to be maintained.
Doesn’t the capital/output ratio fall over time? After all, if there is productivity growth, then the production of capital will also become cheaper. Let’s assume that one farmer with one tractor can produce 500 tons of wheat. It takes a total of 5,000 hours of labor to produce the tractor. If the tractor has a useful life of 10 years, then each ton of wheat requires one hour of capital-producing labor. Now the farmer gets a new tractor, with which he can produce 1000 tons of wheat. If the new tractor also has a useful life of 10 years and required only 7,000 hours of labor to be produced, then each ton of wheat now requires only 0.7 hours of capital-producing labor. The productivity of the new tractor is twice as high but it required only 40% more hours of labor to be produced. If that is a general trend, then the capital/output ratio should fall over time.
Regards. James
Dear James Schipper (at 2014/01/17 at 22:27)
Thanks for your thoughtful comment. In the text, I noted that there is a difference between net and gross investment (the difference between depreciation/replacement). But for simplicity I assume that they are the same. Adding a depreciation component just adds more algebra and it is already difficult enough.
We will discuss changing capital-output ratios soon.
best wishes
bill
Dear Bill
In my opinion, the concept of demographic investment is as useful to know as the concept of demographic momentum or the concept of democratic dividend. Demographic momentum allows us to understand why China may have needed a one-child policy for one generation, and demographic dividend can explain why some Latin American countries are enjoying economic growth even though their productivity per hour is hardly increasing.
Anyway, Alfred Sauvy discusses demographic momentum in Chapter 4 of Section III of his book Éléments de Démographie. Since it seems that you can read German, I can recommend http://www.flassbeck-economics.de
Cheers. James
So, Mr. Schipper, you’re saying there is a flaw in the logic here that would keep a student from progressing to your view? Or is the complexity that will be added to the course necessary, and critical to a 100 level text? As opposed to current texts, I believe simplicity here does not preclude depth. I am a mere dabbler. But maybe you can clearly link the roadblock, or contradiction just a tad clearer for me?