Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – March 21, 2015 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
Only one of the following propositions is possible (with all balances expressed as a per cent of GDP):
- A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending less than they are earning.
- A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning.
- A nation can run a current account deficit with a government sector surplus that is larger, while the private domestic sector is spending less than they are earning.
- None of the above are possible as they all defy the sectoral balances accounting identity.
The answer is Option (b) – A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning.
This is a question about the sectoral balances – the government fiscal balance, the external balance and the private domestic balance – that have to always add to zero because they are derived as an accounting identity from the national accounts.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X – M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I – S) + (G – T) + (X – M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
- The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
- The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
- The Current Account balance (X – M) – positive if in surplus, negative if in deficit.
These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
The following Table represents the three options in percent of GDP terms. To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.
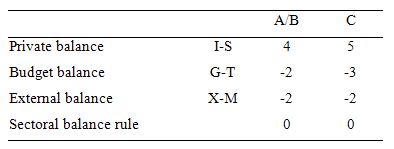
The first two possibilities we might call A and B:
A: A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending less than they are earning.
B: A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning.
So Option A says the private domestic sector is saving overall, whereas Option B say the private domestic sector is dis-saving overall (and increasing its indebtedness). These options are captured in the first column of the Table. So the arithmetic example depicts an external sector deficit of 2 per cent of GDP and an offsetting fiscal surplus of 2 per cent of GDP.
You can see that the private sector balance is positive (that is, the sector is spending more than they are earning – Investment is greater than Saving – and has to be equal to 4 per cent of GDP.
Given that the only proposition that can be true is:
B: A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning.
Column 2 in the Table captures Option C:
C: A nation can run a current account deficit with a government sector surplus that is larger, while the private domestic sector is spending less than they are earning.
So the current account deficit is equal to 2 per cent of GDP while the surplus is now larger at 3 per cent of GDP. You can see that the private domestic deficit rises to 5 per cent of GDP to satisfy the accounting rule that the balances sum to zero.
The final option available is:
D: None of the above are possible as they all defy the sectoral balances accounting identity.
It cannot be true because as the Table data shows the rule that the sectoral balances add to zero because they are an accounting identity is satisfied in both cases.
So what is the economics of this result?
If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down.
The external deficit also means that foreigners are increasing financial claims denominated in the local currency. Given that exports represent a real costs and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.
A fiscal surplus also means the government is spending less than it is “earning” and that puts a drag on aggregate demand and constrains the ability of the economy to grow.
In these circumstances, for income to be stable, the private domestic sector has to spend more than they earn.
You can see this by going back to the aggregate demand relations above. For those who like simple algebra we can manipulate the aggregate demand model to see this more clearly.
Y = GDP = C + I + G + (X – M)
which says that the total national income (Y or GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
So if the G is spending less than it is “earning” and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 2:
One possible problem with running continuous fiscal deficits is that the spending builds up over time and with inflation eventually becoming the risk that has to be managed.
The answer is False.
This question tests whether you understand that fiscal deficits are just the outcome of two flows which have a finite lifespan. Flows typically feed into stocks (increase or decrease them) and in the case of deficits, under current institutional arrangements, they increase public debt holdings.
So the expenditure impacts of deficit exhaust each period and underpin production and income generation and saving. Aggregate saving is also a flow but can add to stocks of financial assets when stored.
Under current institutional arrangements (where governments unnecessarily issue debt to match its net spending $-for-$) the deficits will also lead to a rise in the stock of public debt outstanding. But of-course, the increase in debt is not a consequence of any “financing” imperative for the government. A sovereign government is never revenue constrained because it is the monopoly issuer of the currency.
Flows are like a video that you stream continuously from a camera whereas stocks are like a photo you snap on your camera. Flows are gone once they have passed whereas a stock lingers.
People often think that running a fiscal surplus today provides more capacity to the government to spend tomorrow – as if there is an accumulation process operating. But a fiscal balance is just two flows that are gone once they flow.
A fiscal deficit or surplus observed today provides a currency-issuing government with no extra or no less capacity to spend tomorrow.
So an understanding of stocks and flows helps sort out some furphies.
The following blogs may be of further interest to you:
- Deficit spending 101 – Part 1
- Deficit spending 101 – Part 2
- Deficit spending 101 – Part 3
- Fiscal sustainability 101 – Part 1
- Fiscal sustainability 101 – Part 2
- Fiscal sustainability 101 – Part 3
Question 3:
If employment growth matches the pace of growth in the civilian population (people above 15 years of age) then the economy will experience a constant unemployment rate as long as participation rates do not change.
The answer is True.
The Civilian Population is shorthand for the working age population and can be defined as all people between 15 and 65 years of age or persons above 15 years of age, depending on rules governing retirement. The working age population is then decomposed within the Labour Force Framework (used to collect and disseminate labour force data) into two categories: (a) the Labour Force; and (b) Not in the Labour Force. This demarcation is based on activity principles (willingness, availability and seeking work or being in work).
The participation rate is defined as the proportion of the working age population that is in the labour force. So if the working age population was 1000 and the participation rate was 65 per cent, then the labour force would be 650 persons. So the labour force can vary for two reasons: (a) growth in the working age population – demographic trends; and (b) changes in the participation rate.
The labour force is decomposed into employment and unemployment. To be employed you typically only have to work one hour in the survey week. To be unemployed you have to affirm that you are available, willing and seeking employment if you are not working one hour or more in the survey week. Otherwise, you will be classified as not being in the labour force.
So the hidden unemployed are those who give up looking for work (they become discouraged) yet are willing and available to work. They are classified by the statistician as being not in the labour force. But if they were offered a job today they would immediately accept it and so are in no functional way different from the unemployed.
When economic growth wanes, participation rates typically fall as the hidden unemployed exit the labour force. This cyclical phenomenon acts to reduce the official unemployment rate.
So clearly, the working age population is a much larger aggregate than the labour force and, in turn, employment. Clearly if the participation rate is constant then the labour force will grow at the same rate as the civilian population. And if employment grows at that rate too then while the gap between the labour force and employment will increase in absolute terms (which means that unemployment will be rising), that gap in percentage terms will be constant (that is the unemployment rate will be constant).
The following Table simulates a simple labour market. You can see that while unemployment rises steadily over time the unemployment rate is constant. So as long as employment growth is equal to the growth in the underlying population and the participation rate doesn’t change, the unemployment rate will be constant although more people will be unemployed.
Understanding these aggregates is very important because as we saw in the week just past, the Labour Force data released by the Australian Bureau of Statistics on Thursday has been incorrectly represented in almost all the media coverage. While employment growth was keeping pace with the underlying population the participation rate fell and so the unemployment rate fell. The media focused on the link between the positive employment growth and the declining unemployment and concluded our economy was booming. The reality was very different.
The following blog may be of further interest to you:

“If employment growth matches the pace of growth in the civilian population”
Aargh! “If the rate of growth of employment equals the rate of growth of the civilian population”, then the rate of unemployment will remain constant, provided the participation rate does not change (remains constant).
THAT would have made sense to me.
No wonder all the politicians employ so many spin-meisters! Maybe I’m just too mathematically oriented.
Bill,
Surely the answer to (2) is True.
I get the whole “stock and flow” argument. This issue is the flow of deficit increases the stock of net financial assets (savings) held by the non-government sector. What is the point of savings if not for future consumption? At some point the stock of savings turn into a flow of spending (with associated tax leakages) – if the government continues to run a deficit surely there comes a time when real resources become scarce and the “risk of inflation” occurs.
What have I missed?