Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – March 28, 2015 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
The price at which the central bank provides reserves to the commercial banks is restricted by its target monetary policy rate.
The answer is True.
The facts are as follows. First, central banks will always provided enough reserve balances to the commercial banks at a price it sets using a combination of overdraft/discounting facilities and open market operations.
Second, if the central bank didn’t provide the reserves necessary to match the growth in deposits in the commercial banking system then the payments system would grind to a halt and there would be significant hikes in the interbank rate of interest and a wedge between it and the policy (target) rate – meaning the central bank’s policy stance becomes compromised.
Third, any reserve requirements within this context while legally enforceable (via fines etc) do not constrain the commercial bank credit creation capacity. Central bank reserves (the accounts the commercial banks keep with the central bank) are not used to make loans. They only function to facilitate the payments system (apart from satisfying any reserve requirements).
Fourth, banks make loans to credit-worthy borrowers and these loans create deposits. If the commercial bank in question is unable to get the reserves necessary to meet the requirements from other sources (other banks) then the central bank has to provide them. But the process of gaining the necessary reserves is a separate and subsequent bank operation to the deposit creation (via the loan).
Fifth, if there were too many reserves in the system (relative to the banks’ desired levels to facilitate the payments system and the required reserves then competition in the interbank (overnight) market would drive the interest rate down. This competition would be driven by banks holding surplus reserves (to their requirements) trying to lend them overnight. The opposite would happen if there were too few reserves supplied by the central bank. Then the chase for overnight funds would drive rates up.
In both cases the central bank would lose control of its current policy rate as the divergence between it and the interbank rate widened. This divergence can snake between the rate that the central bank pays on excess reserves (this rate varies between countries and overtime but before the crisis was zero in Japan and the US) and the penalty rate that the central bank seeks for providing the commercial banks access to the overdraft/discount facility.
So the aim of the central bank is to issue just as many reserves that are required for the law and the banks’ own desires.
Now the question seeks to link the penalty rate that the central bank charges for providing reserves to the banks and the central bank’s target rate. The wider the spread between these rates the more difficult does it become for the central bank to ensure the quantity of reserves is appropriate for maintaining its target (policy) rate.
Where this spread is narrow, central banks “hit” their target rate each day more precisely than when the spread is wider.
So if the central bank really wanted to put the screws on commercial bank lending via increasing the penalty rate, it would have to be prepared to lift its target rate in close correspondence. In other words, its monetary policy stance becomes beholden to the discount window settings.
The best answer was false because the central bank cannot operate with wide divergences between the penalty rate and the target rate and it is likely that the former would have to rise significantly to choke private bank credit creation.
You might like to read this blog for further information:
- US federal reserve governor is part of the problem
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
Question 2:
If all national governments simultaneously run public surpluses then it is not possible for all their private domestic sectors to save overall.
The answer is True.
The question tests a knowledge of the sectoral balances and their interactions, the behavioural relationships that generate the flows which are summarised by decomposing the national accounts into these balances, and the constraints that is placed on the behaviour within the three sectors that is evident in the requirement that the balances must add up to zero as a matter of accounting.
Once again, here are the sectoral balances approach to the national accounts.
We can view the basic income-expenditure model in macroeconomics in two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X – M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I – S) + (G – T) + (X – M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
- The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
- The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
- The Current Account balance (X – M) – positive if in surplus, negative if in deficit.
These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances). This is also a basic rule derived from the national accounts and has to apply at all times.
The private domestic sector is only one part of the non-government sector – the other being the external sector.
Most countries currently run external deficits. This means that if the government sector is in surplus the private domestic sector has to be in deficit.
However, some countries have to run external surpluses if there is at least one country running an external deficit. That country can depending on the relative magnitudes of the external balance and private domestic balance, run a public surplus while maintaining strong economic growth. For example, Norway.
In this case an increasing desire to save by the private domestic sector in the face of fiscal drag coming from the fiscal surplus can be offset by a rising external surplus with growth unimpaired. So the decline in domestic spending is compensated for by a rise in net export income.
So if all governments (in all nations) are running public surpluses and some nations are running external deficits (the majority), public surpluses have to be associated (given the underlying behaviour that generates these aggregates) with private domestic deficits.
Even if the external sector balance was zero, the proposition would still be true. At least one private domestic sector would be unable to save overall.
These deficits can keep spending going for a time but the increasing indebtedness ultimately unwinds and households and firms (whoever is carrying the debt) start to reduce their spending growth to try to manage the debt exposure. The consequence is a widening spending gap which pushes the economy into recession and, ultimately, pushes the fiscal balance into deficit via the automatic stabilisers.
So you can sustain economic growth with a private domestic surplus and government surplus if the external surplus is large enough. So a growth strategy can still be consistent with a public surplus. Clearly not every country can adopt this strategy given that the external positions net out to zero themselves across all trading nations. So for every external surplus recorded there has to be equal deficits spread across other nations.
The only way the answer would be False is if all external balances were zero – a never seen outcome.
You might like to read these blogs for further information:
- Sad day for America
- Fiscal austerity – the newest fallacy of composition
- Stock-flow consistent macro models
- Barnaby, better to walk before we run
- Norway and sectoral balances
- The OECD is at it again!
Question 3
From the US National Accounts, you find that in 2006, the share of Personal consumption expenditure in real GDP was 69.9 per cent and by 2008 it had fallen to 69.8 per cent. Similarly, the share of Gross private domestic investment on real GDP was 17.2 per cent in 2006 and by 2008 had fallen to 14.9 per cent (and further to 11.8 per cent in 2009). The net export deficit over the same period (2006 to 2008) fell from -5.7 per cent of real GDP to -4.9 per cent in 2008. Finally, the share of Government consumption expenditures and gross investment in real GDP rose from 18.8 per cent in 2006 to 18.9 per cent in 2008 (and 19.7 per cent in 2009). These relative changes tell you that real GDP was lower in 2008 compared to 2006 because the increase in Government spending and the falling negative contribution of net exports were not sufficient to offset the declining contribution from consumption and investment.
The answer is False.
The detail in the question relates to expenditure shares in real GDP and clearly does not tell you anything about the growth in GDP. All that you are being told are that the shares are changing over the period 2006 to 2008 in favour of public spending.
The shares are given by the following equation:
where A(t) is the value of aggregate A in quarter under consideration (say Personal consumption expenditure) and GDP(t) is the value of GDP in the same quarter.
So a change in the public spending share from 18.8 per cent in 2006 to 18.9 per cent in 2008 just says that in 2008 the flow of public spending is a greater proportion of the flow of real output in 2008 than it was in 2006. The rising share could be associated with a declining, constant or growing real GDP.
The fact you know that over this time that real GDP growth in the US was falling is irrelevant – the question asks whether you can conclude from the information before you.
The other related measure is the contributions to GDP growth which tell you each quarter what the expenditure components contributed to the GDP growth in that quarter.
From the Australian National Accounts – December 2009 you can find the definition of the contributions to GDP growth which is represented by the following equation:
where A(t) is as before; A(t-1) – value of aggregate A in previous quarter; and GDP(t-1) – value of GDP in previous quarter.
The ABS indicate that “the contributions to growth of the components of GDP do not always add exactly to the growth in GDP. This can happen as a result of rounding and the lack of additivity of the chain volume estimates prior to the latest complete financial year.
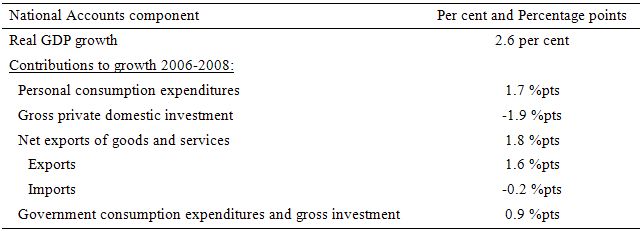
From the US National Accounts data you see that real GDP grew in 2005-06 by 2.7 per cent; then slowed to 2.1 per cent in 2006-07, 0.4 per cent in 2007-08 and plunged to -2.4 per cent in 2008-09. Over the period 2006-2008, real GDP grew overall by 2.6 per cent. The following table breaks down the contributions to that growth by the individual spending components (computed as per the Equation above).
The point of the question (if any) is to warn you into being careful to clarify the concepts being used before drawing conclusions. Too many people think they know what these terms mean and either mis-use them themselves to reach erroneous conclusions or allow themselves to be fooled by others who are touting erroneous conclusions.
If you are interested in more detail on national accounts then the 5216.0 – Australian National Accounts: Concepts, Sources and Methods, 2000 – is the place to go. Recommended reading if you want to get all the concepts and stock-flow relationships really sorted out. The system is universal and used by all statistical agencies.
Q3 was much tougher than usual. It took me a good 10 minutes to figure out just what was being asked!
I can’t claim any credit for getting the right answer. It was a bit of a guess to be honest.
Bill, apologies if this is off topic. Blame it on post-election blues.
You’ve said something like the following many times:
“A currency-issuing government, like Australia, can always run any sized deficit, irrespective of its past fiscal history, if circumstances in the non-government sector warrant. ”
The key word there is CAN. And all your good arguments are designed to show why it CAN.
This leaves the question: so why doesn’t it? I’d like it if you could run a post explaining that.
Regards .. always read your posts and basically agree.
For the second question you say that “The only way the answer would be False is if all external balances were zero – a never seen outcome.” This is something I don’t understand, but I am probably missing something. Doesn’t the question actually comes down to a global perspective and don’t all the external balances net to zero in this case (everybody’s imports are somebody else’s exports)? If all the national governments run surpluses then the total global private domestic sectors together must be in deficit, no matter what the external balances are?
Bill, what is MMT’s view on forex reserves? If you print and swap for other currencies the central bank has a buffer to use in bad times. This may be useful for e.g. developing countries.
I don’t think this is incompatible with MMT.
I think MMT mixes up trade deficit (good) with current account deficit (good.)
I believe the UK had a current account surplus and trade deficit. Is this an ideal situation? You could possibly run trade surpluses and build up foreign currency, businesses, land, etc until becoming having a net importer.
Meant current account deficit (bad.)
BTW, do your MMT models of the economy take into account counterfeiting? It is only a small thing but should be included in economy models.
What is MMT’s view on Russia and the rouble crisis?
Kristof,
I sort of agree with you, except I’d argue that it’s not about the external balances “net(ting) to zero” its the behaviour of each one. So if they were all exactly zero, to the cent, which would mean that every country’s trade was perfectly balanced, then the surplus of each government sector would exactly equal the deficit of each private sector.
This would mean that none of them could save rather than not all of them could save.