Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
The Weekend Quiz – January 23, 2016 – answers and discussion
Here are the answers with discussion for the Weekend quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
Many progressive commentators believe that bank lending should be more closely regulated to ensure that all bank loans were backed by reserves held at the bank. However, this would unnecessarily reduce the capacity of the banks to lend.
The answer is False.
In a “fractional reserve” banking system of the type the US runs (which is really one of the relics that remains from the gold standard/convertible currency era that ended in 1971), the banks have to retain a certain percentage (10 per cent currently in the US) of deposits as reserves with the central bank. You can read about the fractional reserve system from the Federal Point page maintained by the FRNY.
Where confusion as to the role of reserve requirements begins is when you open a mainstream economics textbooks and “learn” that the fractional reserve requirements provide the capacity through which the private banks can create money. The whole myth about the money multiplier is embedded in this erroneous conceptualisation of banking operations.
The FRNY educational material also perpetuates this myth. They say:
If the reserve requirement is 10%, for example, a bank that receives a $100 deposit may lend out $90 of that deposit. If the borrower then writes a check to someone who deposits the $90, the bank receiving that deposit can lend out $81. As the process continues, the banking system can expand the initial deposit of $100 into a maximum of $1,000 of money ($100+$90+81+$72.90+…=$1,000). In contrast, with a 20% reserve requirement, the banking system would be able to expand the initial $100 deposit into a maximum of $500 ($100+$80+$64+$51.20+…=$500). Thus, higher reserve requirements should result in reduced money creation and, in turn, in reduced economic activity.
This is not an accurate description of the way the banking system actually operates and the FRNY (for example) clearly knows their representation is stylised and inaccurate. Later in the same document they they qualify their depiction to the point of rendering the last paragraph irrelevant. After some minor technical points about which deposits count to the requirements, they say this:
Furthermore, the Federal Reserve operates in a way that permits banks to acquire the reserves they need to meet their requirements from the money market, so long as they are willing to pay the prevailing price (the federal funds rate) for borrowed reserves. Consequently, reserve requirements currently play a relatively limited role in money creation in the United States.
In other words, the required reserves play no role in the credit creation process.
The actual operations of the monetary system are described in this way. Banks seek to attract credit-worthy customers to which they can loan funds to and thereby make profit. What constitutes credit-worthiness varies over the business cycle and so lending standards become more lax at boom times as banks chase market share (this is one of Minsky’s drivers).
These loans are made independent of the banks’ reserve positions. Depending on the way the central bank accounts for commercial bank reserves, the latter will then seek funds to ensure they have the required reserves in the relevant accounting period. They can borrow from each other in the interbank market but if the system overall is short of reserves these “horizontal” transactions will not add the required reserves. In these cases, the bank will sell bonds back to the central bank or borrow outright through the device called the “discount window”.
At the individual bank level, certainly the “price of reserves” will play some role in the credit department’s decision to loan funds. But the reserve position per se will not matter. So as long as the margin between the return on the loan and the rate they would have to borrow from the central bank through the discount window is sufficient, the bank will lend.
So the idea that reserve balances are required initially to “finance” bank balance sheet expansion via rising excess reserves is inapplicable. A bank’s ability to expand its balance sheet is not constrained by the quantity of reserves it holds or any fractional reserve requirements. The bank expands its balance sheet by lending. Loans create deposits which are then backed by reserves after the fact. The process of extending loans (credit) which creates new bank liabilities is unrelated to the reserve position of the bank.
The major insight is that any balance sheet expansion which leaves a bank short of the required reserves may affect the return it can expect on the loan as a consequence of the “penalty” rate the central bank might exact through the discount window. But it will never impede the bank’s capacity to effect the loan in the first place.
The money multiplier myth leads students to think that as the central bank can control the monetary base then it can control the money supply. Further, given that inflation is allegedly the result of the money supply growing too fast then the blame is sheeted hometo the “government” (the central bank in this case).
The reality is that the reserve requirements that might be in place at any point in time do not provide the central bank with a capacity to control the money supply.
So would it matter if reserve requirements were 100 per cent? In this blog – 100-percent reserve banking and state banks – I discuss the concept of a 100 per cent reserve system which is favoured by many conservatives who believe that the fractional reserve credit creation process is inevitably inflationary.
There are clearly an array of configurations of a 100 per cent reserve system in terms of what might count as reserves. For example, the system might require the reserves to be kept as gold. In the old “Giro” or “100 percent reserve” banking system which operated by people depositing “specie” (gold or silver) which then gave them access to bank notes issued up to the value of the assets deposited. Bank notes were then issued in a fixed rate against the specie and so the money supply could not increase without new specie being discovered.
Another option might be that all reserves should be in the form of government bonds, which would be virtually identical (in the sense of “fiat creations”) to the present system of central bank reserves.
While all these issues are interesting to explore in their own right, the question does not relate to these system requirements of this type. It was obvious that the question maintained a role for central bank (which would be unnecessary in a 100-per cent reserve system based on gold, for example.
It is also assumed that the reserves are of the form of current current central bank reserves with the only change being they should equal 100 per cent of deposits.
We also avoid complications like what deposits have to be backed by reserves and assume all deposits have to so backed.
In the current system, the the central bank ensures there are enough reserves to meet the needs generated by commercial bank deposit growth (that is, lending). As noted above, the required reserve ratio has no direct influence on credit growth. So it wouldn’t matter if the required reserves were 10 per cent, 0 per cent or 100 per cent.
In a fiat currency system, commercial banks require no reserves to expand credit. Even if the required reserves were 100 per cent, then with no other change in institutional structure or regulations, the central bank would still have to supply the reserves in line with deposit growth.
Now I noted that the central bank might be able to influence the behaviour of banks by imposing a penalty on the provision of reserves. It certainly can do that. As a monopolist, the central bank can set the price and supply whatever volume is required to the commercial banks.
But the price it sets will have implications for its ability to maintain the current policy interest rate which we consider in Question 3.
The central bank maintains its policy rate via open market operations. What really happens when an open market purchase (for example) is made is that the central bank adds reserves to the banking system. This will drive the interest rate down if the new reserve position is above the minimum desired by the banks. If the central bank wants to maintain control of the interest rate then it has to eliminate any efforts by the commercial banks in the overnight interbank market to eliminate excess reserves.
One way it can do this is by selling bonds back to the banks. The same would work in reverse if it was to try to contract the money supply (a la money multiplier logic) by selling government bonds.
The point is that the central bank cannot control the money supply in this way (or any other way) except to price the reserves at a level that might temper bank lending.
So if it set a price of reserves above the current policy rate (as a penalty) then the policy rate would lose traction for reasons explained in the answer to Question 3.
The fact is that it is endogenous changes in the money supply (driven by bank credit creation) that lead to changes in the monetary base (as the central bank adds or subtracts reserves to ensure the “price” of reserves is maintained at its policy-desired level). Exactly the opposite to that depicted in the mainstream money multiplier model.
The other fact is that the money supply is endogenously generated by the horizontal credit (leveraging) activities conducted by banks, firms, investors etc – the central bank is not involved at this level of activity.
You might like to read these blogs for further information:
- Lending is capital- not reserve-constrained
- Oh no … Bernanke is loose and those greenbacks are everywhere
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- 100-percent reserve banking and state banks
- Money multiplier and other myths
Question 2:
Assume a nation is running an external surplus equivalent to 2 per cent of GDP and the private domestic sector is currently saving overall 1 per cent of GDP. In this situation, the government must be running:
(a) A fiscal deficit equal to 1 per cent of GDP.
(b) A fiscal surplus equal to 1 per cent of GDP.
(c) A fiscal deficit equal to 3 per cent of GDP.
(d) A fiscal surplus equal to 3 per cent of GDP.
The answer is Option (B) – A fiscal surplus equal to 1 per cent of GDP.
This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.
We know that from an accounting sense, if the external sector overall is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the accounting rules.
The important point is to understand what behaviour and economic adjustments drive these outcomes.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.
We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all taxes and transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).
Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).
Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):
(2) GNP = C + I + G + (X – M) + FNI
To render this approach into the sectoral balances form, we subtract total taxes and transfers (T) from both sides of Expression (3) to get:
(3) GNP – T = C + I + G + (X – M) + FNI – T
Now we can collect the terms by arranging them according to the three sectoral balances:
(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)
The the terms in Expression (4) are relatively easy to understand now.
The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.
The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).
In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.
The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.
Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.
In English we could say that:
The private financial balance equals the sum of the government financial balance plus the current account balance.
We can re-write Expression (6) in this way to get the sectoral balances equation:
(5) (S – I) = (G – T) + CAD
which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.
Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.
Expression (5) can also be written as:
(6) [(S – I) – CAD] = (G – T)
where the term on the left-hand side [(S – I) – CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.
This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
So what economic behaviour might lead to the outcome specified in the question?
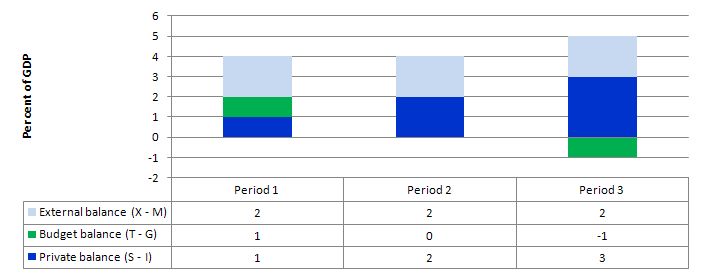
The following graph shows three situations where the external sector is in surplus of 2 per cent of GDP and the private domestic balance is in surplus of varying proportions of GDP (note I have written the fiscal balance as (T – G).
In Period 1, the private domestic balance is in surplus (1 per cent of GDP) and the fiscal balance is also in surplus (1 per cent of GDP). The net injection to demand from the external sector (equivalent to 2 per cent of GDP) is sufficient to “fund” the private saving drain from expenditure without compromising economic growth. The growth in income would also allow the fiscal to be in surplus (via tax revenue).
In Period 2, the rise in private domestic saving drains extra aggregate demand and necessitates a more expansionary position from the government (relative to Period 1), which in this case manifests as a balanced public fiscal position.
Period 3, relates to the data presented in the question – an external surplus of 2 per cent of GDP and private domestic saving equal to 3 per cent of GDP. Now the demand injection from the external sector is being more than offset by the demand drain from private domestic saving. The income adjustments that would occur in this economy would then push the fiscal balance into deficit of 1 per cent of GDP.
The movements in income associated with the spending and revenue patterns will ensure these balances arise.
The general rule is that the government fiscal deficit (surplus) will always equal the non-government surplus (deficit).
So if there is an external surplus that is greater than private domestic sector saving (a surplus) then there will always be a fiscal surplus. Equally, the higher the private saving is relative to the external surplus, the larger the fiscal deficit.
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 3:
Start from a situation where the external surplus is the equivalent of 2 per cent of GDP and the fiscal surplus is 2 per cent of GDP. If the fiscal balance stays constant as a percent of GDP and the external surplus rises to the equivalent of 4 per cent of GDP then:
(a) National income rises and the private domestic surplus moves from 4 per cent of GDP to 6 per cent of GDP.
(b) National income remains unchanged and the private domestic surplus moves from 4 per cent of GDP to 6 per cent of GDP.
(c) National income falls and the private domestic surplus moves from 4 per cent of GDP to 6 per cent of GDP.
(d) National income rises and the private domestic surplus moves from 0 per cent of GDP to 2 per cent of GDP.
(e) National income remains unchanged and the private domestic surplus moves from 0 per cent of GDP to 2 per cent of GDP
(f) National income falls and the private domestic surplus moves from 0 per cent of GDP to 2 per cent of GDP.
The answer is Option (d) National income rises and the private domestic surplus moves from 0 per cent of GDP to 2 per cent of GDP.
Please refer to the explanation in Question 3 for the conceptual material required to understand this question and answer.
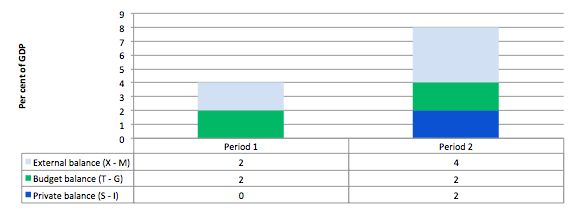
Consider the following graph and accompanying table which depicts two periods outlined in the question.
In Period 1, with an external surplus of 2 per cent of GDP and a fiscal surplus of 2 per cent of GDP the private domestic balance is zero. The demand injection from the external sector is exactly offset by the demand drain (the fiscal drag) coming from the fiscal balance and so the private sector can neither net save or spend more than they earn.
In Period 2, with the external sector adding more to demand now – surplus equal to 4 per cent of GDP and the fiscal balance unchanged (this is stylised – in the real world the fiscal balance will certainly change), there is a stimulus to spending and national income would rise.
The rising national income also provides the capacity for the private sector to save overall and so they can now save 2 per cent of GDP.
The fiscal drag is overwhelmed by the rising net exports.
This is a highly stylised example and you could tell a myriad of stories that would be different in description but none that could alter the basic point.
If the drain on spending (from the public sector) is more than offset by an external demand injection, then GDP rises and the private sector overall saving increases.
If the drain on spending from the fiscal stance outweighs the external injections into the spending stream then GDP falls (or growth is reduced) and the overall private balance would fall into deficit.
You may wish to read the following blogs for more information:
So Bill, can we thus say that the “fractional reserve lending” system does not in reality create the banks’ money supply, the writing of loans? In other words the Fed is also reliant on the “Credit Creation mode”l for making loans as endorsed by the BoE?
Then can we therefore say the fractional reserve system only applies to the government mandated 10% reserve requirement? A separate operation, holding Treasuries at the Fed, which the Fed doesn’t use, just pays interest.
John
What confuse my poor brain is that in order to get (I-S) +(G-T)+(X-M) =0 the signs have to be reversed for the budget and private domestic sector! It seems like the Rubin face/vase effect.
“The other fact is that the money supply is endogenously generated by the horizontal credit (leveraging) activities conducted by banks, firms, investors etc – the central bank is not involved at this level of activity.”
I find this to be a very interesting topic.
It seems that the Fed did get involved at this level at the height of the financial crisis as part of its unusual and possibly illegal activity.
Their reason was the stability of the overall financial system and particularly the money markets.
This vulnerability seems to still be there as this horizontal credit creation (leveraging) seems to be strongly connected to money market funds.