Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
The Weekend Quiz – December 10-11, 2016 – answers and discussion
Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
A program of fiscal austerity (pushing towards surplus) will always undermine attempts by the private domestic sector to reduce its indebtedness when a nation external balance is in deficit.
The answer is True.
Fact – when a nation exports less than they import (including net income flows) we say they have an external deficit (current account deficit).
This is a question about the sectoral balances – the government fiscal balance, the external balance and the private domestic balance – that have to always add to zero because they are derived as an accounting identity from the national accounts. The balances reflect the underlying economic behaviour in each sector which is interdependent – given this is a macroeconomic system we are considering.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
(1) GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.
We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).
Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).
Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):
(2) GNP = C + I + G + (X – M) + FNI
To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:
(3) GNP – T = C + I + G + (X – M) + FNI – T
Now we can collect the terms by arranging them according to the three sectoral balances:
(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)
The the terms in Expression (4) are relatively easy to understand now.
The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.
The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).
In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.
The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.
Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.
In English we could say that:
The private financial balance equals the sum of the government financial balance plus the current account balance.
We can re-write Expression (6) in this way to get the sectoral balances equation:
(5) (S – I) = (G – T) + CAD
which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.
Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.
Expression (5) can also be written as:
(6) [(S – I) – CAD] = (G – T)
where the term on the left-hand side [(S – I) – CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.
This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
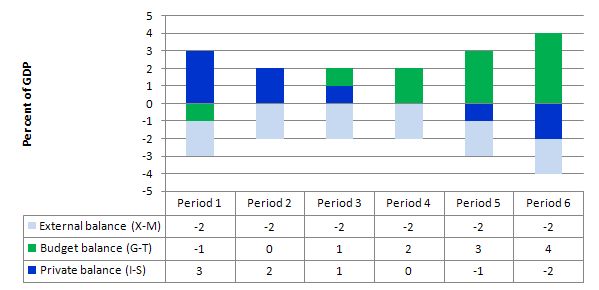
The following graph with accompanying data table lets you see the evolution of the balances expressed in terms of percent of GDP. I have held the external deficit constant at 2 per cent of GDP (which is artificial because as economic activity changes imports also rise and fall).
To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.
If we assume these Periods are average positions over the course of each business cycle (that is, Period 1 is a separate business cycle to Period 2 etc).
In Period 1, there is an external deficit (2 per cent of GDP), a fiscal surplus of 1 per cent of GDP and the private sector is in deficit (I > S) to the tune of 3 per cent of GDP.
In Period 2, as the government fiscal balance enters balance (presumably the government increased spending or cut taxes or the automatic stabilisers were working), the private domestic deficit narrows and now equals the external deficit. This is the case that the question is referring to.
This provides another important rule with the deficit terorists typically overlook – that if a nation records an average external deficit over the course of the business cycle (peak to peak) and you succeed in balancing the public fiscal balance then the private domestic sector will be in deficit equal to the external deficit.
That means, the private sector is increasingly building debt to fund its “excess expenditure”. That conclusion is inevitable when you balance a fiscal outcome with an external deficit. It could never be a viable fiscal rule.
With an external deficit, it is impossible for both the government and the private domestic sector to reduce their overall debt levels by spending less than they earn.
It might be argued that the private domestic sector could still reduce debt even though they are spending more than they are earning through asset sales. That is true but a finite solution. Soon enough all assets would be sold and the flow realities would persist.
In Periods 3 and 4, the fiscal deficit rises from balance to 1 to 2 per cent of GDP and the private domestic balance moves towards surplus. At the end of Period 4, the private sector is spending as much as they earning.
Periods 5 and 6 show the benefits of fiscal deficits when there is an external deficit. The private sector now is able to generate surpluses overall (that is, save as a sector) as a result of the public deficit.
So what is the economics that underpin these different situations?
If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down.
The external deficit also means that foreigners are increasing financial claims denominated in the local currency. Given that exports represent a real cost and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.
A fiscal surplus also means the government is spending less than it is “earning” and that puts a drag on aggregate demand and constrains the ability of the economy to grow.
In these circumstances, for income to be stable, the private domestic sector has to spend more than they earn.
You can see this by going back to the aggregate demand relations above. For those who like simple algebra we can manipulate the aggregate demand model to see this more clearly.
Y = GDP = C + I + G + (X – M)
which says that the total national income (Y or GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
So if the G is spending less than it is “earning” and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income.
Only when the government fiscal deficit supports aggregate demand at income levels which permit the private sector to save out of that income will the latter achieve its desired outcome. At this point, income and employment growth are maximised and private debt levels will be stable.
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 2:
A rising level of bank reserves will make it easier for banks to expand credit to the private sector if the demand for loans increases.
The answer is False.
This is a question about whether you understand the flawed concept of the money multiplier.
Mainstream macroeconomics textbooks present a flawed depiction of the credit-creation capacity of commercial banks. The concept of the money multiplier is at the centre of this analysis and posits that the multiplier m transmits changes in the so-called monetary base (MB) (the sum of bank reserves and currency at issue) into changes in the money supply (M). The chapters on money usually present some arcane algebra which is deliberately designed to impart a sense of gravitas or authority to the students who then mindlessly ape what is in the textbook.
They rehearse several times in their undergraduate courses (introductory and intermediate macroeconomics; money and banking; monetary economics etc) the mantra that the money multiplier is usually expressed as the inverse of the required reserve ratio plus some other novelties relating to preferences for cash versus deposits by the public.
Accordingly, the students learn that if the central bank told private banks that they had to keep 10 per cent of total deposits as reserves then the required reserve ratio (RRR) would be 0.10 and m would equal 1/0.10 = 10. More complicated formulae are derived when you consider that people also will want to hold some of their deposits as cash. But these complications do not add anything to the story.
The formula for the determination of the money supply is: M = m x MB. So if a $1 is newly deposited in a bank, the money supply will rise (be multiplied) by $10 (if the RRR = 0.10). The way this multiplier is alleged to work is explained as follows (assuming the bank is required to hold 10 per cent of all deposits as reserves):
- A person deposits say $100 in a bank.
- To make money, the bank then loans the remaining $90 to a customer.
- They spend the money and the recipient of the funds deposits it with their bank.
- That bank then lends 0.9 times $90 = $81 (keeping 0.10 in reserve as required).
- And so on until the loans become so small that they dissolve to zero
None of this is accurate in terms of depicting how the banks make loans. It is an important device for the mainstream because it implies that banks take deposits to get funds which they can then on-lend. But prudential regulations require they keep a little in reserve. So we get this credit creation process ballooning out due to the fractional reserve requirements.
The money multiplier myth also leads students to think that as the central bank can control the monetary base then it can control the money supply. Further, given that inflation is allegedly the result of the money supply growing too fast then the blame is sheeted hometo the “government”. This leads to claims that if the government runs a fiscal deficit then it has to issue bonds to avoid causing hyperinflation. Nothing could be further from the truth.
That is nothing like the way the banking system operates in the real world. The idea that the monetary base (the sum of bank reserves and currency) leads to a change in the money supply via some multiple is not a valid representation of the way the monetary system operates.
First, the central bank does not have the capacity to control the money supply in a modern monetary system. In the world we live in, bank loans create deposits and are made without reference to the reserve positions of the banks. The bank then ensures its reserve positions are legally compliant as a separate process knowing that it can always get the reserves from the central bank. The only way that the central bank can influence credit creation in this setting is via the price of the reserves it provides on demand to the commercial banks.
Second, this suggests that the decisions by banks to lend may be influenced by the price of reserves rather than whether they have sufficient reserves. They can always get the reserves that are required at any point in time at a price, which may be prohibitive.
Third, the money multiplier story has the central bank manipulating the money supply via open market operations. So they would argue that the central bank might buy bonds to the public to increase the money base and then allow the fractional reserve system to expand the money supply. But a moment’s thought will lead you to conclude this would be futile unless (as in Question 3 a support rate on excess reserves equal to the current policy rate was being paid).
Why? The open market purchase would increase bank reserves and the commercial banks, in lieu of any market return on the overnight funds, would try to place them in the interbank market. Of-course, any transactions at this level (they are horizontal) net to zero so all that happens is that the excess reserve position of the system is shuffled between banks. But in the process the interbank return would start to fall and if the process was left to resolve, the overnight rate would fall to zero and the central bank would lose control of its monetary policy position (unless it was targetting a zero interest rate).
In lieu of a support rate equal to the target rate, the central bank would have to sell bonds to drain the excess reserves. The same futility would occur if the central bank attempted to reduce the money supply by instigating an open market sale of bonds.
In all cases, the central bank cannot influence the money supply in this way.
Fourth, given that the central bank adds reserves on demand to maintain financial stability and this process is driven by changes in the money supply as banks make loans which create deposits. Banks do not initially need reserves to lend. Reserves are used to facilitate the integrity of the clearing house (payments system). The links below provide more in-depth analysis of that point.
So the operational reality is that the dynamics of the monetary base (MB) are driven by the changes in the money supply which is exactly the reverse of the causality presented by the monetary multiplier.
So in fact we might write MB = M/m, where m is a divisor.
You might like to read these blogs for further information:
- Teaching macroeconomics students the facts
- Lost in a macroeconomics textbook again
- Lending is capital- not reserve-constrained
- Oh no … Bernanke is loose and those greenbacks are everywhere
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- 100-percent reserve banking and state banks
- Money multiplier and other myths
Question 3:
The public debt ratio is of no concern because economic growth will always bring it down after a recession.
The answer is False.
First, the public debt ratio is of no concern per se if the nation is sovereign in its own currency. But the question was probing whether you understand the dynamics of the ratio in relation to GDP growth.
The primary deficit may not fall when economic growth is positive if discretionary policy changes offset the declining net spending as tax revenue increases and welfare payments fall (the automatic stabilisation).
Under current institutional arrangements, governments around the world voluntarily issue debt into the private bond markets to match $-for-$ their net spending flows in each period. A sovereign government within a fiat currency system does not have to issue any debt and could run continuous fiscal deficits (that is, forever) with a zero public debt.
The reason they is covered in the following blogs – On voluntary constraints that undermine public purpose.
The framework for considering this question is provided by the accounting relationship linking the fiscal flows (spending, taxation and interest servicing) with relevant stocks (base money and government bonds).
This framework has been interpreted by the mainstream macroeconommists as constituting an a priori financial constraint on government spending (more on this soon) and by proponents of Modern Monetary Theory (MMT) as an ex post accounting relationship that has to be true in a stock-flow consistent macro model but which carries no particular import other than to measure the changes in stocks between periods. These changes are also not particularly significant within MMT given that a sovereign government is never revenue constrained because it is the monopoly issuer of the currency.
To understand the difference in viewpoint we might usefully start with the mainstream view. The way the mainstream macroeconomics textbooks build this narrative is to draw an analogy between the household and the sovereign government and to assert that the microeconomic constraints that are imposed on individual or household choices apply equally without qualification to the government. The framework for analysing these choices has been called the government budget constraint (GBC) in the literature.
The GBC is in fact an accounting statement relating government spending and taxation to stocks of debt and high powered money. However, the accounting character is downplayed and instead it is presented by mainstream economists as an a priori financial constraint that has to be obeyed. So immediately they shift, without explanation, from an ex post sum that has to be true because it is an accounting identity, to an alleged behavioural constraint on government action.
The GBC is always true ex post but never represents an a priori financial constraint for a sovereign government running a flexible-exchange rate non-convertible currency. That is, the parity between its currency and other currencies floats and the the government does not guarantee to convert the unit of account (the currency) into anything else of value (like gold or silver).
This literature emerged in the 1960s during a period when the neo-classical microeconomists were trying to gain control of the macroeconomic policy agenda by undermining the theoretical validity of the, then, dominant Keynesian macroeconomics. There was nothing particularly progressive about the macroeconomics of the day which is known as Keynesian although as I explain in this blog – Those bad Keynesians are to blame – that is a bit of a misnomer.
Anyway, just as an individual or a household is conceived in orthodox microeconomic theory to maximise utility (real income) subject to their fiscal constraints, this emerging approach also constructed the government as being constrained by a fiscal or “financing” constraint. Accordingly, they developed an analytical framework whereby the fiscal deficits had stock implications – this is the so-called GBC.
So within this model, taxes are conceived as providing the funds to the government to allow it to spend. Further, this approach asserts that any excess in government spending over taxation receipts then has to be “financed” in two ways: (a) by borrowing from the public; and (b) by printing money.
You can see that the approach is a gold standard approach where the quantity of “money” in circulation is proportional (via a fixed exchange price) to the stock of gold that a nation holds at any point in time. So if the government wants to spend more it has to take money off the non-government sector either via taxation of bond-issuance.
However, in a fiat currency system, the mainstream analogy between the household and the government is flawed at the most elemental level. The household must work out the financing before it can spend. The household cannot spend first. The government can spend first and ultimately does not have to worry about financing such expenditure.
From a policy perspective, they believed (via the flawed Quantity Theory of Money) that “printing money” would be inflationary (even though governments do not spend by printing money anyway. So they recommended that deficits be covered by debt-issuance, which they then claimed would increase interest rates by increasing demand for scarce savings and crowd out private investment. All sorts of variations on this nonsense has appeared ranging from the moderate Keynesians (and some Post Keynesians) who claim the “financial crowding out” (via interest rate increases) is moderate to the extreme conservatives who say it is 100 per cent (that is, no output increase accompanies government spending).
So the GBC is the mainstream macroeconomics framework for analysing these “financing” choices and it says that the fiscal deficit in year t is equal to the change in government debt (ΔB) over year t plus the change in high powered money (ΔH) over year t. If we think of this in real terms (rather than monetary terms), the mathematical expression of this is written as:
which you can read in English as saying that Budget deficit (BD) = Government spending (G) – Tax receipts (T) + Government interest payments (rBt-1), all in real terms.
However, this is merely an accounting statement. It has to be true if things have been added and subtracted properly in accounting for the dealings between the government and non-government sectors.
In mainstream economics, money creation is erroneously depicted as the government asking the central bank to buy treasury bonds which the central bank in return then prints money. The government then spends this money. This is called debt monetisation and we have shown in the Deficits 101 series how this conception is incorrect. Anyway, the mainstream claims that if the government is willing to increase the money growth rate it can finance a growing deficit but also inflation because there will be too much money chasing too few goods! But an economy constrained by deficient demand (defined as demand below the full employment level) responds to a nominal impulse by expanding real output not prices.
But because they believe that inflation is inevitable if “printing money” occurs, mainstream economists recommend that governments use debt issuance to “finance” their deficits. But then they scream that this will merely require higher future taxes. Why should taxes have to be increased?
Well the textbooks are full of elaborate models of debt pay-back, debt stabilisation etc which all “prove” (not!) that the legacy of past deficits is higher debt and to stabilise the debt, the government must eliminate the deficit which means it must then run a primary surplus equal to interest payments on the existing debt.
Nothing is included about the swings and roundabouts provided by the automatic stabilisers as the results of the deficits stimulate private activity and welfare spending drops and tax revenue rises automatically in line with the increased economic growth. Most orthodox models are based on the assumption of full employment anyway, which makes them nonsensical depictions of the real world.
More sophisticated mainstream analyses focus on the ratio of debt to GDP rather than the level of debt per se. They come up with the following equation – nothing that they now disregard the obvious opportunity presented to the government via ΔH. So in the following model all net public spending is covered by new debt-issuance (even though in a fiat currency system no such financing is required).
Accordingly, the change in the public debt ratio is:
The change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP.
A growing economy can absorb more debt and keep the debt ratio constant. For example, if the primary deficit is zero, debt increases at a rate r but the debt ratio increases at r – g.
So a change in the change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP.
As we noted a growing economy can absorb more debt and keep the debt ratio constant. For example, if the primary deficit is zero, debt increases at a rate r but the debt ratio increases at r – g.
Consider the following table which simulates two different scenarios. Case A shows a real interest rate of zero and a steadily increasing annual GDP growth rate across 10 years. The initial public debt ratio is 100 per cent (so well over the level Reinhart and Rogoff claim is the point of no return and insolvency is pending). The fiscal deficit is also simulated to be 5 per cent of GDP then reduces as the GDP growth induce the automatic stabilisers. It then reaches a steady 2 per cent per annum which might be sufficient to support the saving intentions of the non-government sector while still promoting steady economic growth.
You can see that the even with a continuous deficit, the public debt ratio declines steadily and would continue to do so as the growth continued. The central bank could of-course cut the nominal interest rate to speed the contraction in the debt ratio although I would not undertake that policy change for that reason.
In Case B we assume that the government stops issuing debt with everything else the same. The public debt ratio drops very quickly under this scenario.
However, should the real interest rate exceed the economic growth rate, then unless the primary fiscal balance offsets the rising interest payments as percent of GDP, then the public debt ratio will rise.
The only concern I would have in this situation does not relate to the rising ratio. Focusing on the cause should be the policy concern. If the real economy is faltering because interest rates are too high or more likely because the primary fiscal deficit is too low then the rising public debt ratio is just telling us that the central bank should drop interest rates or the treasury should increase the discretionary component of the fiscal balance.
In general though, the public debt ratio is a relatively uninteresting macroeconomic figure and should be disregarded. If the government is intent on promoting growth, then the primary deficit ratio and the public debt ratio will take care of themselves.
You may be interested in reading these blogs which have further information on this topic:

Once again, I’m confused. If a monetary sovereign has a monopoly over the money supply, why can’t it exert some control over M2, or whatever measure is used? I get that the private banking system can increase spending by lending to customers. But isn’t there a dollar for dollar creation of debt by their loans? This would seem to be a change in composition, rather than an increase in the money supply. The banks create money but that money is equaled by a debt instrument. It sounds to me exactly like what the US does now, issuing debt dollar for dollar for net spending. Injecting debt free money into the private economy, which is what a sovereign can do, appears to me to be a direct addition to the money supply. What happens if the government does not rollover its debt? Is the money supply reduced as the debt is reduced?
What I wonder is how central banks supply reserves in the case of national surpluses.
Chris,
Sovereign debt only denotes the amount of reserves that have been sequestered into bonds (bond sales/redemption only change the composition, it is spending/taxation which impact the total sum of the two). If government does not “roll over its debt” this simply results in an abundance of reserves, in which case the interest rate will fall to zero. Conventional theory would have us believe this would result in an explosion of the money supply due to the “money multiplier”, but that is false – the level of reserves does not impact the ability or likelihood of banks to extend loans, ergo monetary policy does not “control the money supply”.
Government can increase or decrease the supply of dollars in circulation through its *fiscal* powers, by spending (taxing). Barring extremes, this may or may not increase (decrease) the “total” money in circulation when bank lending is taken into account. While bank lending is overall “net zero”, credit expansion does expand the amount of dollars currently circulating, and this dynamic in aggregate leads to booms and busts – it depends on the balance between loans created and loans paid, and which way that balance is trending.