Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
The Weekend Quiz – April 8-9, 2017 – answers and discussion
Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
The private domestic sector cannot save if a nation’s external sector is in balance (and thus making no contribution to real GDP growth) and the government runs a balanced fiscal position.
The answer is False.
Read the words correctly. We are asking whether the private domestic sector cannot generate a flow of saving in a given accounting period when the fiscal position is balanced and the economy is effectively closed (external balance). This is distinct from the notion of saving overall as a sector, which relates to whether the private domestic sector is spending more than it is earning.
This is a question about sectoral balances. Skip the derivation if you are familiar with the framework.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
(1) GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.
We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).
Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).
Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):
(2) GNP = C + I + G + (X – M) + FNI
To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:
(3) GNP – T = C + I + G + (X – M) + FNI – T
Now we can collect the terms by arranging them according to the three sectoral balances:
(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)
The the terms in Expression (4) are relatively easy to understand now.
The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.
The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).
In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.
The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.
Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.
In English we could say that:
The private financial balance equals the sum of the government financial balance plus the current account balance.
We can re-write Expression (6) in this way to get the sectoral balances equation:
(5) (S – I) = (G – T) + CAD
which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.
Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.
Expression (5) can also be written as:
(6) [(S – I) – CAD] = (G – T)
where the term on the left-hand side [(S – I) – CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.
This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
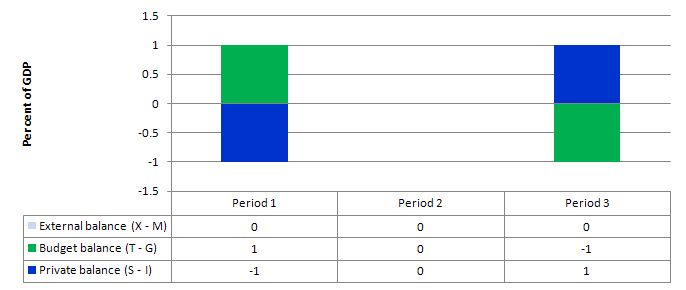
Consider the following graph which shows three situations where the external sector is in balance.
Period 1, the fiscal position is in surplus (T – G = 1) and the private balance is in deficit (S – I = -1). This means that the private domestic sector is spending more (via consumption and investment taken together) than it is earning. So it is dissaving overall. Note that households could still be saving (that is, not spending all of their disposable income). But as a sector, the combination of firms and households would be dissaving.
With the external balance equal to 0, the general rule that the government surplus (deficit) equals the non-government deficit (surplus) applies to the government and the private domestic sector.
In Period 3, the fiscal position is in deficit (T – G = -1) and this provides some demand stimulus in the absence of any impact from the external sector, which allows the private domestic sector to save (S – I = 1).
Period 2, is the case in point and the sectoral balances show that if the external sector is in balance and the government is able to achieve a fiscal balance, then the private domestic sector must also be in balance. This means that the private domestic sector is spending exactly what they earn and so overall are not saving.
The movements in income associated with the spending and revenue patterns will ensure these balances arise. The problem is that if the private domestic sector desires to save overall then this outcome will be unstable and would lead to changes in the other balances as national income changed in response to the decline in private spending.
So under the conditions specified in the question, the private domestic sector cannot save overall. The government would be undermining any desire to save by not providing the fiscal stimulus necessary to increase national output and income so that private households/firms could save overall.
You may wish to read the following blogs for more information:
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
- Barnaby, better to walk before we run
- Saturday Quiz – June 19, 2010 – answers and discussion
Question 2:
If the household saving ratio rises and there is an external deficit then government must increase net spending to fill the private spending gap or else national output and income will fall.
The answer is False.
This is another examination of the sectoral sectoral balances logic used in Question 1. The secret to getting the correct answer is to realise that the household saving ratio is not the overall sectoral balance for the private domestic sector.
In other words, if you just compared the household saving ratio with the external deficit and the fiscal balance you would be leaving an essential component of the private domestic balance out – private capital formation (investment).
Taking the summary balances equation as a starting point in $ values:
(S – I) = (G – T) + CAD
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents and include net income flows.
You can then manipulate these balances to tell stories about what is going on in a country.
For example, when an external deficit (CAD < 0) and a public surplus (G – T < 0) coincide, there must be a private deficit. So if X = 10 and M = 20, (and there are zero net income flows), the CAD = -10 (a current account deficit). Also if G = 20 and T = 30, G – T = -10 (a fiscal surplus). So the right-hand side of the sectoral balances equation will equal (20 – 30) + (10 – 20) = -20.
As a matter of accounting then (S – I) = -20 which means that the domestic private sector is spending more than they are earning because I > S by 20 (whatever $ units we like). So the fiscal drag from the public sector is coinciding with an influx of net savings from the external sector. While private spending can persist for a time under these conditions using the net savings of the external sector, the private sector becomes increasingly indebted in the process. It is an unsustainable growth path.
So if a nation usually has a current account deficit (CAD < 0) then if the private domestic sector is to net save (S – I) > 0, then the public fiscal deficit has to be large enough to offset the current account deficit. Say, (X – M) = -20 (as above). Then a balanced fiscal position (G – T = 0) will force the domestic private sector to spend more than they are earning (S – I) = -20. But a government deficit of 25 (for example, G = 55 and T = 30) will give a right-hand solution of (55 – 30) + (10 – 20) = 15. The domestic private sector can net save.
We use the term net save to refer to the saving overall of the sector (that is, the surplus of income above spending) rather than the saving flow that might be generated by households when they consume less than disposable income.
So by only focusing on the household saving ratio in the question, I was only referring to one component of the private domestic balance. Clearly in the case of the question, if private investment is strong enough to offset the household desire to increase saving (and withdraw from consumption) then no spending gap arises.
In the present situation in most countries, households have reduced the growth in consumption (as they have tried to repair overindebted balance sheets) at the same time that private investment has fallen dramatically.
As a consequence a major spending gap emerged that could only be filled in the short- to medium-term by government deficits if output growth was to remain intact. The reality is that the fiscal deficits were not large enough and so income adjustments (negative) occurred and this brought the sectoral balances in line at lower levels of economic activity.
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 3:
Rising yields on 10-year bond yields rising signify that the bond markets are demanding increased risk premiums for these assets.
The answer is False.
While it might be possible that bond markets are demanding an increased risk coverage on 10-year bonds one cannot conclude that from merely examining the movements in bond yields. That is because yields fluctuate for several reasons.
The only thing that one can reliably conclude (which isn’t saying much at all) is that yields are rising because bond prices are falling in response to lower demand.
In macroeconomics, we summarise the plethora of public debt instruments with the concept of a bond. The standard bond has a face value – say $A1000 and a coupon rate – say 5 per cent and a maturity – say 10 years. This means that the bond holder will will get $50 dollar per annum (interest) for 10 years and when the maturity is reached they would get $1000 back.
Bonds are issued by government into the primary market, which is simply the institutional machinery via which the government sells debt to “raise funds”. In a modern monetary system with flexible exchange rates it is clear the government does not have to finance its spending so the the institutional machinery is voluntary and reflects the prevailing neo-liberal ideology – which emphasises a fear of fiscal excesses rather than any intrinsic need.
Once bonds are issued they are traded in the secondary market between interested parties. Clearly secondary market trading has no impact at all on the volume of financial assets in the system – it just shuffles the wealth between wealth-holders. In the context of public debt issuance – the transactions in the primary market are vertical (net financial assets are created or destroyed) and the secondary market transactions are all horizontal (no new financial assets are created). Please read my blog – Deficit spending 101 – Part 3 – for more discussion on this point.
Further, most primary market issuance is now done via auction. Accordingly, the government would determine the maturity of the bond (how long the bond would exist for), the coupon rate (the interest return on the bond) and the volume (how many bonds) being specified.
The issue would then be put out for tender and the market then would determine the final price of the bonds issued. Imagine a $1000 bond had a coupon of 5 per cent, meaning that you would get $50 dollar per annum until the bond matured at which time you would get $1000 back.
Imagine that the market wanted a yield of 6 per cent to accommodate risk expectations (inflation or something else). So for them the bond is unattractive and they would avoid it under the tap system. But under the tender or auction system they would put in a purchase bid lower than the $1000 to ensure they get the 6 per cent return they sought.
The mathematical formulae to compute the desired (lower) price is quite tricky and you can look it up in a finance book.
The general rule for fixed-income bonds is that when the prices rise, the yield falls and vice versa. Thus, the price of a bond can change in the market place according to interest rate fluctuations.
When interest rates rise, the price of previously issued bonds fall because they are less attractive in comparison to the newly issued bonds, which are offering a higher coupon rates (reflecting current interest rates).
When interest rates fall, the price of older bonds increase, becoming more attractive as newly issued bonds offer a lower coupon rate than the older higher coupon rated bonds.
Further, rising yields may indicate a rising sense of risk (mostly from future inflation although sovereign credit ratings will influence this).
But they may also indicated a recovering economy where people are more confidence investing in commercial paper (for higher returns) and so they demand less of the “risk free” government paper.
So you see how an event (yield rises) that signifies growing confidence in the real economy is reinterpreted (and trumpeted) by the conservatives to signal something bad (crowding out). In this case, the reason long-term yields would be rising is because investors were diversifying their portfolios and moving back into private financial assets.
The yield reflects the last auction bid in the bond issue. So if diversification is occurring reflecting confidence and the demand for public debt weakens and yields rise this has nothing at all to do with a declining pool of funds being soaked up by the binging government!
The following blogs may be of further interest to you:
- Saturday Quiz – April 17, 2010 – answers and discussion
- Time to outlaw the credit rating agencies
- Studying macroeconomics – an exercise in deception
- Time for a reality check on debt – Part 1
- Will we really pay higher interest rates?
That is enough for today!
(c) Copyright 2017 William Mitchell. All Rights Reserved.
‘Read the words correctly. ‘ Fell foul of that one! I didn’t distinguish between ‘domestic sector cannot save’ and ‘domestic sector cannot save on aggregate.’
Second one had me fooled. For some reason i still fail to understand what is understood with investment or private capital formation.
Willem – I too get a bit confused on the ‘investment’ issues as i find it hard to distinguish it from ‘consumption’ at times as investment is still ‘buying things.’ (e.g. buying machinery for a business etc) so why isn’t it subsumed under ‘C’?
Investment is usually connected with something that ‘adds value’ so I suppose if a buy a computer for my home, that’s consumption but if I buy it for my business office that is ‘investment.’
I get blurred around the edges with this!
Yes, same here