Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
The Weekend Quiz – February 17-18, 2018 – answers and discussion
Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
If the growth in wages (the money you get paid) keeps pace with inflation which is accelerating at the same rate as labour productivity is growing then the wage share in GDP remains constant.
The answer is True.
The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.
To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.
Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.
The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.
So the wage bill = W.L
The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.
Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:
LP = GDP/L
so it tells us what real output (GDP) each labour unit that is added to production produces on average.
We can also define another term that is regularly used in the media – the real wage – which is the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).
We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.
Macroeconomics is hard to learn because it involves these abstract variables that are never observed – like the price level, like “the interest rate” etc. They are just stylisations of the general tendency of all the different prices and interest rates.
Now the nominal wage (W) – that is paid by employers to workers is determined in the labour market – by the contract of employment between the worker and the employer. The price level (P) is determined in the goods market – by the interaction of total supply of output and aggregate demand for that output although there are complex models of firm price setting that use cost-plus mark-up formulas with demand just determining volume sold. We shouldn’t get into those debates here.
The inflation rate is just the continuous growth in the price level (P). A once-off adjustment in the price level is not considered by economists to constitute inflation.
So the real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).
We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.
Nominal GDP ($GDP) can be written as P.GDP, where the P values the real physical output.
Now if you put of these concepts together you get an interesting framework.
To help you follow the logic here are the terms developed and be careful not to confuse $GDP (nominal) with GDP (real):
- Wage share = (W.L)/$GDP
- Nominal GDP: $GDP = P.GDP
- Labour productivity: LP = GDP/L
- Real wage: w = W/P
By substituting the expression for Nominal GDP into the wage share measure we get:
Wage share = (W.L)/P.GDP
In this area of economics, we often look for alternative way to write this expression – it maintains the equivalence (that is, obeys all the rules of algebra) but presents the expression (in this case the wage share) in a different “view”.
So we can write as an equivalent:
Wage share – (W/P).(L/GDP)
Now if you note that (L/GDP) is the inverse (reciprocal) of the labour productivity term (GDP/L). We can use another rule of algebra (reversing the invert and multiply rule) to rewrite this expression again in a more interpretable fashion.
So an equivalent but more convenient measure of the wage share is:
Wage share = (W/P)/(GDP/L) – that is, the real wage (W/P) divided by labour productivity (GDP/L).
I won’t show this but I could also express this in growth terms such that if the growth in the real wage equals labour productivity growth the wage share is constant. The algebra is simple but we have done enough of that already.
That journey might have seemed difficult to non-economists (or those not well-versed in algebra) but it produces a very easy to understand formula for the wage share.
Two other points to note. The wage share is also equivalent to the real unit labour cost (RULC) measures that Treasuries and central banks use to describe trends in costs within the economy. Please read my blog – Saturday Quiz – May 15, 2010 – answers and discussion – for more discussion on this point.
Now it becomes obvious that if the nominal wage (W) and the price level (P) are growing at the pace the real wage is constant. And if the real wage is growing at the same rate as labour productivity, then both terms in the wage share ratio are equal and so the wage share is constant.
The wage share was constant for a long time during the Post Second World period and this constancy was so marked that Kaldor (the Cambridge economist) termed it one of the great “stylised” facts. So real wages grew in line with
productivity growth which was the source of increasing living standards for workers.
The productivity growth provided the “room” in the distribution system for workers to enjoy a greater command over real production and thus higher living standards without threatening inflation.
Since the mid-1980s, the neo-liberal assault on workers’ rights (trade union attacks; deregulation; privatisation; persistently high unemployment) has seen this nexus between real wages and labour productivity growth broken. So while real wages have been stagnant or growing modestly, this growth has been dwarfed by labour productivity growth.
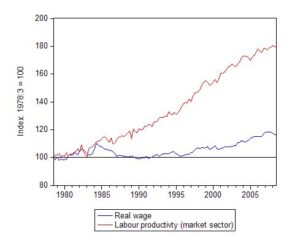
In this blog – The origins of the economic crisis – I provided these graphs. First, the movement real wages and labour productivity since 1979. Both series are indexed to 100 as at the September quarter 1978. So by September 2008, the real wage index had climbed to 116.7 (that is, around 15 per cent growth in just over 12 years) but the labour productivity index was 179.1.
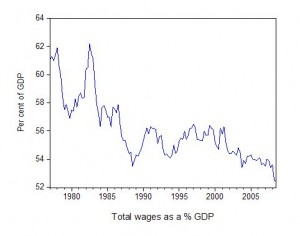
This suggests from our discussion that the wage share should have fallen. That is what the next graph depicts – it shows how far the wage share has fallen in Australia over the last two decades. The trend has been common across the globe during the neo-liberal years and is one of the pre-conditions that explain our current economic crisis.
The following blogs may be of further interest to you:
Question 2:
The expansionary impact of deficit spending on aggregate demand is lower when the government matches the deficit with debt-issuance because then excess reserves are drained and the purchasing power is taken out of the monetary system.
The answer is False.
The mainstream macroeconomic textbooks all have a chapter on fiscal policy (and it is often written in the context of the so-called IS-LM model but not always).
The chapters always introduces the so-called Government Budget Constraint that alleges that governments have to “finance” all spending either through taxation; debt-issuance; or money creation. The writer fails to understand that government spending is performed in the same way irrespective of the accompanying monetary operations.
They claim that money creation (borrowing from central bank) is inflationary while the latter (private bond sales) is less so. These conclusions are based on their erroneous claim that “money creation” adds more to aggregate demand than bond sales, because the latter forces up interest rates which crowd out some private spending.
All these claims are without foundation in a fiat monetary system and an understanding of the banking operations that occur when governments spend and issue debt helps to show why.
So what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a fiscal deficit without issuing debt?
Like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.
The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made. Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet). Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.
This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management. The aim of the central bank is to “hit” a target interest rate and so it has to ensure that competitive forces in the interbank market do not compromise that target.
When there are excess reserves there is downward pressure on the overnight interest rate (as banks scurry to seek interest-earning opportunities), the central bank then has to sell government bonds to the banks to soak the excess up and maintain liquidity at a level consistent with the target. Some central banks offer a return on overnight reserves which reduces the need to sell debt as a liquidity management operation.
There is no sense that these debt sales have anything to do with “financing” government net spending. The sales are a monetary operation aimed at interest-rate maintenance. So M1 (deposits in the non-government sector) rise as a result of the deficit without a corresponding increase in liabilities. It is this result that leads to the conclusion that that deficits increase net financial assets in the non-government sector.
What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.
The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).
There is no difference to the impact of the deficits on net worth in the non-government sector.
Mainstream economists would say that by draining the reserves, the central bank has reduced the ability of banks to lend which then, via the money multiplier, expands the money supply.
However, the reality is that:
- Building bank reserves does not increase the ability of the banks to lend.
- The money multiplier process so loved by the mainstream does not describe the way in which banks make loans.
- Inflation is caused by aggregate demand growing faster than real output capacity. The reserve position of the banks is not functionally related with that process.
So the banks are able to create as much credit as they can find credit-worthy customers to hold irrespective of the operations that accompany government net spending.
This doesn’t lead to the conclusion that deficits do not carry an inflation risk. All components of aggregate demand carry an inflation risk if they become excessive, which can only be defined in terms of the relation between spending and productive capacity.
It is totally fallacious to think that private placement of debt reduces the inflation risk. It does not.
You may wish to read the following blogs for more information:
- Why history matters
- Building bank reserves will not expand credit
- Building bank reserves is not inflationary
- The complacent students sit and listen to some of that
- Saturday Quiz – February 27, 2010 – answers and discussion
Question 3:
A government is choosing between a tax cut that will reduce tax revenue at the current level of national income by $x (that is, increase private domestic disposable income by $x) and a public spending increase of $x. Which policy option will have the greater initial impact on aggregate spending?
(a) Tax cut
(b) Spending increase
(c) Both will be equivalent
(d) There is not enough information to answer this question
The answer is Spending increase.
The question is only seeking an understanding of the initial injection into the spending stream rather than the fully exhausted multiplied expansion of national income that will result. It is clear that the tax cut approach will have two effects: (a) some initial demand stimulus; and (b) it increases the value of the multiplier, other things equal.
We are only interested in the first effect rather than the total effect. But I will give you some insight also into what the two components of the tax result might imply overall when compared to the stimulus motivated by an increase in government spending.
To give you a concrete example which will consolidate the understanding of what happens, imagine that the marginal propensity to consume out of disposable income is 0.8 and there is only one tax rate set at 0.20. So for every extra dollar that the economy produces the government taxes 20 cents leaving 80 cents in disposable income. In turn, households then consume 0.8 of this 80 cents which means an injection of 64 cents goes into aggregate demand which them multiplies as the initial spending creates income which, in turn, generates more spending and so on.
Government spending increase
An increase in government spending (say of $1000) is what we call an exogenous injection into the spending stream and stimulates aggregate demand by that amount. So it might be an order of $1000 worth of gadget X which advances human welfare immeasurably! The firm that produces gadget X thus increases production of the good or service by the rise in orders ($1000) and as a result incomes of the productive factors rises by $1000. So the initial rise in aggregate demand is $1000.
This initial increase in national output and income then stimulates (induces) further consumption by 64 cents in the dollar so in Period 2, aggregate demand increases by $640. Output and income rises by the same amount to meet this increase in spending. In Period 3, aggregate demand rises by 0.8 x 0.8 x $640 and so on. The induced spending increase gets smaller and smaller because some of each round of income increase is taxed away, some goes to imports and some is saved.
Tax-cut induced stimulus
The stimulus coming from a tax-cut does not directly impact on the spending stream in the same way as the rise in government spending.
First, imagine the government worked out a tax cut that would increase its initial fiscal deficit by the same amount as would have been the case if it had increased government spending (so in our example, $1000).
In other words, disposable income at each level of GDP rises initially by $1000. What happens next?
Some of the disposable income is saved (20 cents in each dollar that disposable income increases). So immediately some of the tax increase is lost from the spending stream.
In this case the injection into aggregate demand is $800 rather than $1000 in the case of the increase in government spending.
What happens next depends on the parameters of the macroeconomic system. The multiplied rise in national income may be higher or lower depending on these parameters. But it will never be the case that an initial fiscal equivalent tax cut will be more stimulatory than a government spending increase.
Note in answering this question I am disregarding all the nonsensical notions of Ricardian equivalence that abound among the mainstream doomsayers who have never predicted anything of empirical note! All their predictions come to nought.
You may wish to read the following blogs for more information:
That is enough for today!
(c) Copyright 2018 William Mitchell. All Rights Reserved.
I don’t understand the answer to q1.
All we know is that real wages stay the same , that the rate of inflation is accelerating and that labor productivity is growing. The fact that inflation is accelerating seems irrelevant as we know that real wages are constant. Other things equal constant real wages combined with increased productivity would lead to a falling share of wages (more stuff is being produced so workers, who get the same amount of stuff, get a smaller share of this bigger pile of stuff so it seems that the profit share will increase not remain constant. But we don’t know if other things are equal are not so I gave the answer as ‘Cannot tell from this information’.
Did I mis-read the question ?
Don’t know why I started talking about profit share ! I meant that wage share will fall not remain constant.
Rob, I came up with the same answer for the same reasons as you on question 1. I don’t think you mis-read it. Seems to me the answer ‘true’ would only apply if the productivity growth rate was zero.
Hi- I have the same comment, that given the tricky nature of the questions on this quiz generally, we are right to read question 1 closely, and it does not bear the interpretation that the putative answer puts on it.
The question implies that the wage share is rising only on pace with inflation, but *not* with labor productivity. But it also says that the latter is rising at the same rate as inflation. Thus the wage share is going down, not staying the same. “If the growth in wages (the money you get paid) keeps pace with inflation…”
Thanks for your tireless efforts!
I dusted off my School C algebra and worked through the wage share formula with some hypothetical numbers and now I get it better.
I think adding hypothetical numbers with that stuff helps dullards like me understand better.
It’s quite complicated to conceptualise how inflation, real wages and productivity interact – ratios etc do my head in.
I probably need more maths.
Dear Burk braun (at 2018/02/20 at 2:51 am)
No, the question doesn’t imply the wage share is rising with inflation. It is the nominal wage rate that is rising with inflation – in other words, the real wage is constant.
The wage rate is not the share.
best wishes
bill
If the govt. buys gold it doesn’t count as gdp.
😉
The quiz question from yesterday is DIFFERENT from the quizz question you answer!
1. If the growth in wages (the money you get paid) keeps pace with inflation which is accelerating at the same rate as labour productivity is growing then the profit share in GDP remains constant.
NOTE: “… profit share in GDP remains constant.” Then you prove that wage share remains constant in today’s answer.
This is not a serious grumble. I’m amazed you find the time to create this very informative site.