The Weekend Quiz – October 5-6, 2019 – answers and discussion

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

If there is more “money” in the economy its value inevitably declines.

The answer is False.

The falsehood enters as a result of the qualifier ‘inevitably’. There are situations where more ‘money’ will reduce its value but it is not inevitable.

The question requires you to: (a) understand the difference between bank reserves and the money supply; and (b) understand the Quantity Theory of Money.

The mainstream macroeconomics text book argument that increasing the money supply will cause inflation is based on the Quantity Theory of Money. First, expanding bank reserves will put more base money into the economy but not increase the aggregates that drive the alleged causality in the Quantity Theory of Money – that is, the various estimates of the “money supply”.

Second, even if the money supply is increasing, the economy may still adjust to that via output and income increases up to full capacity. Over time, as investment expands the productive capacity of the economy, aggregate demand growth can support the utilisation of that increased capacity without there being inflation.

In this situation, an increasing money supply (which is really not a very useful aggregate at all) which signals expanding credit will not be inflationary.

So the Maybe relates to the situation that might arise if nominal demand kept increasing beyond the capacity of the real economy to absorb it via increased production. Then you would get inflation and the “value” of the dollar would start to decline.

The Quantity Theory of Money which in symbols is MV = PQ but means that the money stock times the turnover per period (V) is equal to the price level (P) times real output (Q). The mainstream assume that V is fixed (despite empirically it moving all over the place) and Q is always at full employment as a result of market adjustments.

In applying this theory the mainstream deny the existence of unemployment. The more reasonable mainstream economists admit that short-run deviations in the predictions of the Quantity Theory of Money can occur but in the long-run all the frictions causing unemployment will disappear and the theory will apply.

In general, the Monetarists (the most recent group to revive the Quantity Theory of Money) claim that with V and Q fixed, then changes in M cause changes in P – which is the basic Monetarist claim that expanding the money supply is inflationary. They say that excess monetary growth creates a situation where too much money is chasing too few goods and the only adjustment that is possible is nominal (that is, inflation).

One of the contributions of Keynes was to show the Quantity Theory of Money could not be correct. He observed price level changes independent of monetary supply movements (and vice versa) which changed his own perception of the way the monetary system operated.

Further, with high rates of capacity and labour underutilisation at various times (including now) one can hardly seriously maintain the view that Q is fixed. There is always scope for real adjustments (that is, increasing output) to match nominal growth in aggregate demand. So if increased credit became available and borrowers used the deposits that were created by the loans to purchase goods and services, it is likely that firms with excess capacity will react to the increased nominal demand by increasing output.

The mainstream have related the current non-standard monetary policy efforts – the so-called quantitative easing – to the Quantity Theory of Money and predicted hyperinflation will arise.

So it is the modern belief in the Quantity Theory of Money is behind the hysteria about the level of bank reserves at present – it has to be inflationary they say because there is all this money lying around and it will flood the economy.

Textbook mislead their students into thinking that there is a direct relationship between the monetary base and the money supply. They claim that the central bank “controls the money supply by buying and selling government bonds in open-market operations” and that the private banks then create multiples of the base via credit-creation.

Please read my blog – Money multiplier and other myths – for more discussion on this point.

The idea that the monetary base (the sum of bank reserves and currency) leads to a change in the money supply via some multiple is not a valid representation of the way the monetary system operates even though it appears in all mainstream macroeconomics textbooks and is relentlessly rammed down the throats of unsuspecting economic students.

The money multiplier myth leads students to think that as the central bank can control the monetary base then it can control the money supply. Further, given that inflation is allegedly the result of the money supply growing too fast then the blame is sheeted home to the “government” (the central bank in this case).

The reality is that the central bank does not have the capacity to control the money supply. We have regularly traversed this point. In the world we live in, bank loans create deposits and are made without reference to the reserve positions of the banks. The bank then ensures its reserve positions are legally compliant as a separate process knowing that it can always get the reserves from the central bank.

The only way that the central bank can influence credit creation in this setting is via the price of the reserves it provides on demand to the commercial banks.

So when we talk about quantitative easing, we must first understand that it requires the short-term interest rate to be at zero or close to it. Otherwise, the central bank would not be able to maintain control of a positive interest rate target because the excess reserves would invoke a competitive process in the interbank market which would effectively drive the interest rate down.

Quantitative easing then involves the central bank buying assets from the private sector – government bonds and high quality corporate debt. So what the central bank is doing is swapping financial assets with the banks – they sell their financial assets and receive back in return extra reserves. So the central bank is buying one type of financial asset (private holdings of bonds, company paper) and exchanging it for another (reserve balances at the central bank). The net financial assets in the private sector are in fact unchanged although the portfolio composition of those assets is altered (maturity substitution) which changes yields and returns.

In terms of changing portfolio compositions, quantitative easing increases central bank demand for “long maturity” assets held in the private sector which reduces interest rates at the longer end of the yield curve. These are traditionally thought of as the investment rates. This might increase aggregate demand given the cost of investment funds is likely to drop. But on the other hand, the lower rates reduce the interest-income of savers who will reduce consumption (demand) accordingly.

How these opposing effects balance out is unclear but the evidence suggests there is not very much impact at all.

For the monetary aggregates (outside of base money) to increase, the banks would then have to increase their lending and create deposits. This is at the heart of the mainstream belief is that quantitative easing will stimulate the economy sufficiently to put a brake on the downward spiral of lost production and the increasing unemployment. The recent experience (and that of Japan in 2001) showed that quantitative easing does not succeed in doing this.

This should come as no surprise at all if you understand Modern Monetary Theory (MMT).

The mainstream view is based on the erroneous belief that the banks need reserves before they can lend and that quantitative easing provides those reserves. That is a major misrepresentation of the way the banking system actually operates. But the mainstream position asserts (wrongly) that banks only lend if they have prior reserves.

The illusion is that a bank is an institution that accepts deposits to build up reserves and then on-lends them at a margin to make money. The conceptualisation suggests that if it doesn’t have adequate reserves then it cannot lend. So the presupposition is that by adding to bank reserves, quantitative easing will help lending.

But banks do not operate like this. Bank lending is not “reserve constrained”. Banks lend to any credit worthy customer they can find and then worry about their reserve positions afterwards. If they are short of reserves (their reserve accounts have to be in positive balance each day and in some countries central banks require certain ratios to be maintained) then they borrow from each other in the interbank market or, ultimately, they will borrow from the central bank through the so-called discount window. They are reluctant to use the latter facility because it carries a penalty (higher interest cost).

The point is that building bank reserves will not increase the bank’s capacity to lend. Loans create deposits which generate reserves.

The reason that the commercial banks are currently not lending much is because they are not convinced there are credit worthy customers on their doorstep. In the current climate the assessment of what is credit worthy has become very strict compared to the lax days as the top of the boom approached.

Those that claim that quantitative easing will expose the economy to uncontrollable inflation are just harking back to the old and flawed Quantity Theory of Money.

This theory has no application in a modern monetary economy and proponents of it have to explain why economies with huge excess capacity to produce (idle capital and high proportions of unused labour) cannot expand production when the orders for goods and services increase. Should quantitative easing actually stimulate spending then the depressed economies will likely respond by increasing output not prices.

So the fact that large scale quantitative easing conducted by central banks in Japan in 2001 and now in the UK and the USA has not caused inflation does not provide a strong refutation of the mainstream Quantity Theory of Money because it has not impacted on the monetary aggregates.

The fact that is hasn’t is not surprising if you understand how the monetary system operates but it has certainly bedazzled the (easily dazzled) mainstream economists.

So as long as the nominal growth of spending (and money) is keeping pace with the real capacity of the economy to produce goods and services then there will be no dimunition in the ‘value’ of money.

The following blog posts may be of further interest to you:

• Money multiplier and other myths
• Islands in the sun
• Operation twist – then and now
• Quantitative easing 101
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary

Question 2:

If there was a fiscal rule imposed such that the national government had to balance its fiscal position at all times then this would also eliminate the sensitivity of the fiscal outcome to the automatic stabilisers.

The answer is False.

The final fiscal outcome is the difference between total federal revenue and total federal outlays. So if total revenue is greater than outlays, the fiscal outcome is in surplus and vice versa. It is a simple matter of accounting with no theory involved. However, the fiscal balance is used by all and sundry to indicate the fiscal stance of the government.

So if the fiscal outcome is in surplus it is often concluded that the fiscal impact of government is contractionary (withdrawing net spending) and if the fiscal outcome is in deficit we say the fiscal impact expansionary (adding net spending).

Further, a rising deficit (falling surplus) is often considered to be reflecting an expansionary policy stance and vice versa. What we know is that a rising deficit may, in fact, indicate a contractionary fiscal stance – which, in turn, creates such income losses that the automatic stabilisers start driving the fiscal outcome back towards (or into) deficit.

So the complication is that we cannot conclude that changes in the fiscal impact reflect discretionary policy changes. The reason for this uncertainty clearly relates to the operation of the automatic stabilisers.

To see this, the most simple model of the fiscal balance we might think of can be written as:

Fiscal Balance = Revenue – Spending = (Tax Revenue + Other Revenue) – (Welfare Payments + Other Spending)

We know that Tax Revenue and Welfare Payments move inversely with respect to each other, with the latter rising when GDP growth falls and the former rises with GDP growth. These components of the fiscal balance are the so-called automatic stabilisers.

In other words, without any discretionary policy changes, the fiscal balance will vary over the course of the business cycle. When the economy is weak – tax revenue falls and welfare payments rise and so the fiscal balance moves towards deficit (or an increasing deficit). When the economy is stronger – tax revenue rises and welfare payments fall and the fiscal balance becomes increasingly positive. Automatic stabilisers attenuate the amplitude in the business cycle by expanding the fiscal outcome in a recession and contracting it in a boom.

So just because the fiscal outcome goes into deficit doesn’t allow us to conclude that the Government has suddenly become of an expansionary mind. In other words, the presence of automatic stabilisers make it hard to discern whether the fiscal policy stance (chosen by the government) is contractionary or expansionary at any particular point in time.

The first point to always be clear about then is that the fiscal balance is not determined by the government. Its discretionary policy stance certainly is an influence but the final outcome will reflect non-government spending decisions. In other words, the concept of a fiscal rule – where the government can set a desired balance (in the case of the question – zero) and achieve that at all times is fraught.

It is likely that in attempting to achieve a balanced fiscal outcome the government will set its discretionary policy settings counter to the best interests of the economy – either too contractionary or too expansionary.

If there was a balanced fiscal rule and private spending fell dramatically then the automatic stabilisers would push the fiscal outcome into the direction of deficit. The final outcome would depend on net exports and whether the private sector was saving overall or not. Assume, that net exports were in deficit (typical case) and private saving overall was positive. Then private spending declines.

In this case, the actual fiscal outcome would be a deficit equal to the sum of the other two balances.

Then in attempting to apply the fiscal rule, the discretionary component of the fiscal outcome would have to contract. This contraction would further reduce aggregate demand and the automatic stabilisers (loss of tax revenue and increased welfare payments) would be working against the discretionary policy choice.

In that case, the application of the fiscal rule would be undermining production and employment and probably not succeeding in getting the fiscal outcome into balance.

But every time a discretionary policy change was made the impact on aggregate demand and hence production would then trigger the automatic stabilisers via the income changes to work in the opposite direction to the discretionary policy shift.

You might like to read these blog posts for further information:

• Structural deficits and automatic stabilisers
• Structural deficits – the great con job!

Question 3:

The private domestic sector will always run a deficit (spend more than they earn) exactly equal to the external deficit on average over a complete economic cycle, if the government fiscal position averages out to zero over the same cycle.

The answer is True.

This is a question about the sectoral balances – the government fiscal balance, the external balance and the private domestic balance – that have to always add to zero because they are derived as an accounting identity from the national accounts. The balances reflect the underlying economic behaviour in each sector which is interdependent – given this is a macroeconomic system we are considering.

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

(1) GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAB

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAB > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAB < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.

Expression (5) can also be written as:

(6) [(S – I) – CAB] = (G – T)

where the term on the left-hand side [(S – I) – CAB] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.

This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

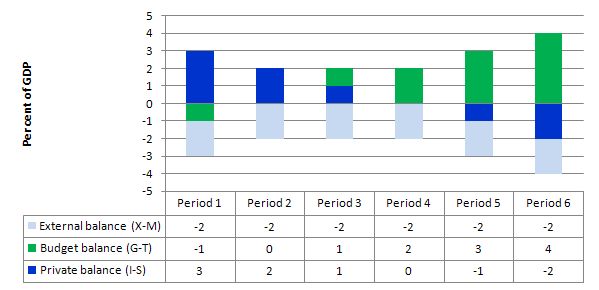
The following graph with accompanying data table lets you see the evolution of the balances expressed in terms of percent of GDP. I have held the external deficit constant at 2 per cent of GDP (which is artificial because as economic activity changes imports also rise and fall).

To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.

If we assume these Periods are average positions over the course of each business cycle (that is, Period 1 is a separate business cycle to Period 2 etc).

In Period 1, there is an external deficit (2 per cent of GDP), a fiscal surplus of 1 per cent of GDP and the private sector is in deficit (I > S) to the tune of 3 per cent of GDP.

In Period 2, as the government fiscal outcome enters balance (presumably the government increased spending or cut taxes or the automatic stabilisers were working), the private domestic deficit narrows and now equals the external deficit. This is the case that the question is referring to.

This provides another important rule with the deficit terrorists typically overlook – that if a nation records an average external deficit over the course of the business cycle (peak to peak) and you succeed in balancing the public fiscal outcome then the private domestic sector will be in deficit equal to the external deficit. That means, the private sector is increasingly building debt to fund its “excess expenditure”. That conclusion is inevitable when you balance a fiscal outcome with an external deficit. It could never be a viable fiscal rule.

In Periods 3 and 4, the fiscal deficit rises from balance to 1 to 2 per cent of GDP and the private domestic balance moves towards surplus. At the end of Period 4, the private sector is spending as much as they earning.

Periods 5 and 6 show the benefits of fiscal deficits when there is an external deficit. The private sector now is able to generate surpluses overall (that is, save as a sector) as a result of the public deficit.

So what is the economics that underpin these different situations?

If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down.

The external deficit also means that foreigners are increasing financial claims denominated in the local currency. Given that exports represent a real cost and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.

A fiscal surplus also means the government is spending less than it is “earning” and that puts a drag on aggregate demand and constrains the ability of the economy to grow.

In these circumstances, for income to be stable, the private domestic sector has to spend more than they earn.

You can see this by going back to the aggregate demand relations above. For those who like simple algebra we can manipulate the aggregate demand model to see this more clearly.

Y = GDP = C + I + G + (X – M)

which says that the total national income (Y or GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

So if the G is spending less than it is “earning” and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income.

Only when the government fiscal deficit supports aggregate demand at income levels which permit the private sector to save out of that income will the latter achieve its desired outcome. At this point, income and employment growth are maximised and private debt levels will be stable.

The following blog posts may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

That is enough for today!

(c) Copyright 2019 William Mitchell. All Rights Reserved.