Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
The Weekend Quiz – March 28-29, 2020 – answers and discussion
Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
Only one of the following propositions is possible (with all balances expressed as a per cent of GDP):
(a) A nation can run an external deficit with a fiscal surplus of equal proportion to GDP, while the private domestic sector is spending less than they are earning.
(b) A nation can run an external deficit with a fiscal surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning.
(c) A nation can run an external deficit with a fiscal surplus that is a larger proportion of GDP, while the private domestic sector is spending less than they are earning.
(d) None of the above are possible as they all defy the sectoral balances accounting identity.
The correct answer is Option (b).
This is a question about the sectoral balances – the government fiscal balance, the external balance and the private domestic balance – that have to always add to zero because they are derived as an accounting identity from the national accounts.
To refresh your memory the sectoral balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.
We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all taxes and transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).
Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).
Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):
(2) GNP = C + I + G + (X – M) + FNI
To render this approach into the sectoral balances form, we subtract total taxes and transfers (T) from both sides of Expression (3) to get:
(3) GNP – T = C + I + G + (X – M) + FNI – T
Now we can collect the terms by arranging them according to the three sectoral balances:
(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)
The the terms in Expression (4) are relatively easy to understand now.
The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.
The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).
In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.
The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.
Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.
In English we could say that:
The private financial balance equals the sum of the government financial balance plus the current account balance.
We can re-write Expression (6) in this way to get the sectoral balances equation:
(5) (S – I) = (G – T) + CAB
which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAB > 0) generate national income and net financial assets for the private domestic sector.
Conversely, government surpluses (G – T < 0) and current account deficits (CAB < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.
Expression (5) can also be written as:
(6) [(S – I) – CAB] = (G – T)
where the term on the left-hand side [(S – I) – CAB] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.
This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
The following Table represents the three options in percent of GDP terms. To aid interpretation remember that (S-I) < 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.
| Sectoral Balance | Interpretation of Result | Case A | Case B |
| External (X – M) | Deficit is negative | -2 | -2 |
| Fiscal (G – T) | Deficit is positive | -2 | -3 |
| Private Domestic (S – I) | Deficit is negative | -4 | -5 |
| Sectoral Balance Rule | 0 | 0 |
Case A shows that when the external deficit is equal to the fiscal surplus (per cent of GDP), the private domestic sector has to be spending more than its income (S < I).
So Option (a) cannot be correct.
Case B shows that when when the external deficit is less than the fiscal surplus (as per cent of GDP), the private domestic sector has to be spending more than its income (S < I).
So Option (c) cannot be correct.
Given that the only proposition that can be true is:
A nation can run an external deficit with a fiscal surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning.
The final option available is:
None of the above are possible as they all defy the sectoral balances accounting identity.
It cannot be true because as the Table data shows the rule that the sectoral balances add to zero because they are an accounting identity is satisfied in both cases.
So what is the economics of this result?
If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down.
The external deficit also means that foreigners are increasing financial claims denominated in the local currency. Given that exports represent a real costs and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.
A fiscal surplus also means the government is spending less than it is “earning” and that puts a drag on aggregate demand and constrains the ability of the economy to grow.
In these circumstances, for income to be stable, the private domestic sector has to spend more than they earn.
You can see this by going back to the aggregate demand relations above. For those who like simple algebra we can manipulate the aggregate demand model to see this more clearly.
Y = GDP = C + I + G + (X – M)
which says that the total national income (Y or GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
So if the G is spending less than it is “earning” and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income
The following blog posts may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 2:
It won’t be long before the European Commission demands that Eurozone nations are forced to pursue internal devaluation through austerity programs that are designed to deflate nominal wages and prices to allegedly improve their relative competitiveness. Ignoring whether the logic is correct or not, which of the following propositions must also follow within the internal devaluation logic:
(a) If wages and prices fall at the same rate, then labour productivity has to rise and employment remain constant or grow.
(b) If wages and prices fall at the same rate, then labour productivity has to rise and employment must grow.
(c) If wages and prices fall at the same rate, then labour productivity has to rise and what happens to employment is irrelevant.
(d) None of the above
The correct answer is Option (c).
The EMU countries cannot improve their international competitiveness by exchange rate depreciation, which is the option always available to a fully sovereign nation issuing its own currency and floating it in foreign exchange markets.
Thus, to improve their international competitiveness, the EMU countries have to engage in “internal devaluation” which means they have to cut real unit labour costs – which are the real cost of producing goods and services. Governments setting out on this policy path have to engineer cuts in the wage and price levels (the latter following the former as unit costs fall).
But the question demonstrates that it takes more than just a nominal deflation. The strategy hinges on whether you can also engineer productivity growth (typically).
So given the assumption (wage and prices falling at the same rate), the correct answer is:
If wages and prices fall at the same rate, then labour productivity has to rise and what happens to employment is irrelevant.
Some explanatory notes to accompany the analysis that follows:
- Employment is measured in persons (averaged over the period).
- Labour productivity is the units of output per person employment per period.
- The wage and price level are in nominal units; the real wage is the wage level divided by the price level and tells us the real purchasing power of that nominal wage level.
- The wage bill is employment times the wage level and is the total labour costs in production for each period.
- Real GDP is thus employment times labour productivity and represents a flow of actual output per period; Nominal GDP is Real GDP at market value – that is, multiplied by the price level. So real GDP can grow while nominal GDP can fall if the price level is deflating and productivity growth and/or employment growth is positive.
- The wage share is the share of total wages in nominal GDP and is thus a guide to the distribution of national income between wages and profits.
- Unit labour costs are in nominal terms and are calculated as total labour costs divided by nominal GDP. So they tell you what each unit of output is costing in labour outlays; Real unit labour costs just divide this by the price level to give a real measure of what each unit of output is costing. RULC is also the ratio of the real wage to labour productivity and through algebra I would be able to show you (trust me) that it is equivalent to the Wage share measure (although I have expressed the latter in percentage terms and left the RULC measure in raw units).
The following table models the constant and growing productivity cases but holds employment constant for five periods.
We assume that the nominal wage and the price level deflate by 10 per cent per period over Period 2 to 5. In the productivity growth case, we assume it grows by 10 per cent per period over Period 2 to 5.
It is quite clear that under the assumptions employed, RULC cannot fall without productivity growth. The only other way to accomplish this is to ensure that nominal wages fall faster than the price level falls.
In the historical debate, this was a major contention between Keynes and Pigou (an economist in the neo-classical tradition who best represented the so-called “British Treasury View” in the 1930s.
The Treasury View thought the cure to the Great Depression was to cut the real wage because according to their erroneous logic, unemployment could only occur if the real wage was too high.
Keynes argued that if you tried to cut nominal wages as a way of cutting the real wage (given there is no such thing as a real wage that policy can directly manipulate), firms will be forced by competition to cut prices to because unit labour costs would be lower.
He hypothesised that there is no reason not to believe that the rate of deflation in nominal wage and price level would be similar and so the real wage would be constant over the period of the deflation. So that is the operating assumption here.
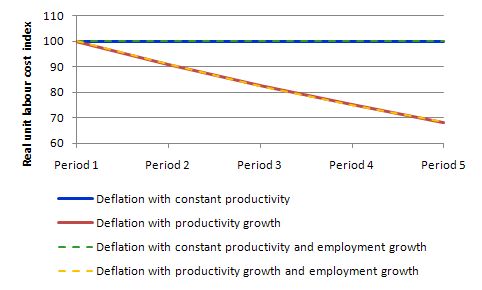
The following table models the constant and growing productivity cases as above but allows employment to grow by 10 per cent per period.
All four scenarios in the Table are them modelled in the following graph with the Real Unit Labour Costs converted into index number form equal to 100 in Period 1.
As you can see what happens to employment makes no difference at all.
I could have also modelled employment falling with the same results.
The following graph shows the four scenarios shown in the last two tables.
I have dashed some scenarios to make the lines visible (given that Case A and Case C) are equivalent as are Case B and Case D.
What you learn is that if wages and prices fall at the same rate and labour productivity does not rise there can be no reduction in unit or real unit labour costs.
So the internal devaluation strategy relies heavily on productivity growth occurring.
The literature on organisational psychology and industrial relations is replete of examples where worker morale is an important ingredient in accomplishing productivity growth.
In a climate of austerity characteristic of an internal devaluation strategy it is highly likely that productivity will not grow and may even fall over time. Then the internal devaluation strategy is useless.
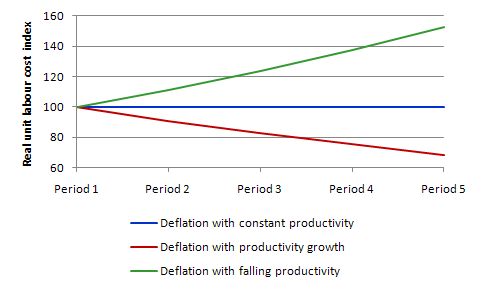
This graph compares the two scenarios in the first Table with the more realistic one that labour productivity actually falls as the government ravages the economy in pursuit of its internal devaluation.
As you can see real unit labour costs rise as labour productivity falls and the economy’s competitiveness (given the exchange rate is fixed) falls.
Of-course, this “supply-side” scenario does not take into account the overwhelming reality that for an economy to realise this level of output over an extended period aggregate demand would have to be supportive. The internal devaluation strategy relies heavily on the external sector providing the demand impetus.
The following blog posts may be of further interest to you:
- Euro zone’s self-imposed meltdown
- A Greek tragedy …
- España se está muriendo
- Exiting the Euro?
- Doomed from the start
- Europe – bailout or exit?
- Not the EMF … anything but the EMF!
- EMU posturing provides no durable solution
- Protect your workers for the sake of the nation
- The bullies and the bullied
- Modern monetary theory in an open economy
Question 3:
One possible problem with running continuous fiscal deficits is that the spending builds up over time and with inflation eventually becoming the risk that has to be managed.
The answer is False.
This question tests whether you understand that fiscal deficits are just the outcome of two flows which have a finite lifespan. Flows typically feed into stocks (increase or decrease them) and in the case of deficits, under current institutional arrangements, they increase public debt holdings.
So the expenditure impacts of deficit exhaust each period and underpin production and income generation and saving. Aggregate saving is also a flow but can add to stocks of financial assets when stored.
Under current institutional arrangements (where governments unnecessarily issue debt to match its net spending $-for-$) the deficits will also lead to a rise in the stock of public debt outstanding. But of-course, the increase in debt is not a consequence of any “financing” imperative for the government. A sovereign government is never revenue constrained because it is the monopoly issuer of the currency.
The following blog posts may be of further interest to you:
- Deficit spending 101 – Part 1
- Deficit spending 101 – Part 2
- Deficit spending 101 – Part 3
- Fiscal sustainability 101 – Part 1
- Fiscal sustainability 101 – Part 2
- Fiscal sustainability 101 – Part 3
That is enough for today!
(c) Copyright 2020 William Mitchell. All Rights Reserved.


I really like this Quiz format Bill. It’s a great way to learn. Thanks.